Solution des exercices : les composés aromatiques
Exercice 1
a. Bromobenzène
b. Ethyl benzene
c. Clyclobutylbenzène
d. $1$, $2$, $3$-trimétyibenzène
e. $1$, $2$, $4$-trinitrobenzène
f. $1$, $3$, $5$-trimétyibenzène
g. $11$,$2$ -difluorobenzène
h. $3$-nitrophénol
i. $1$-Méthyléthyl-$4$-propylbenzène
j. Méthylbenzène ou toluène
k. $1$,$2$-diméthylbenzène ou orthodiméthylbenzène
2. Donnons la formule semi-développée des composés aromatiques
$2.1.1. 3,5$-triméthylbenzène
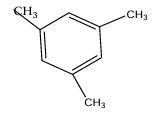
2.2. $11$-bromo-$4$-chlorobenzène
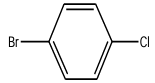
2.3. Fluorobenzène
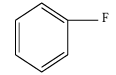
2.4. $1.4$-dibromo-$2$-méthylbenzène
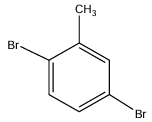
2.5. Hexylbenzène
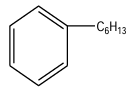
Exercice 2
Composés aromatiques
1. Formule développée du styrène.
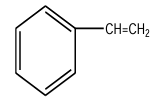
a. Équations-bilans de toutes les réactions mises en jeu dans cette manipulation.
a. Équations-bilans de toutes les réactions mises en jeu dans cette manipulation.
$C_{6}H_{6}+Br_{2}\longrightarrow_{\lim FeBr_{3}}C_{6}H_{5}Br+HBr$
$C_{8}H_{8}+Br_{2}\longrightarrow_{\lim FeBr_{3}}C_{8}H_{7}Br+HBr$
$C_{8}H_{7}Br+Br_{2}\longrightarrow_{\lim FeBr_{3}}C_{8}H_{7}Br_{3}$
$Ag^{+}+Br^{-}\longrightarrow AgBr$
b. Détermination des compositions molaire et volumique du mélange étudié.
$C_{6}H_{6}+Br_{2}\longrightarrow_{\lim FeBr_{3}}C_{6}H_{5}Br+HBr$
$x\quad\quad x\quad\quad\quad x\quad\quad x$
$C_{8}H_{8}+Br_{2}\longrightarrow_{\lim FeBr_{3}}C_{8}H_{7}Br+HBr$
$Y\quad\quad Y\quad\quad\quad Y\quad\quad Y$
$C_{8}H_{7}Br+Br_{2}\longrightarrow_{\lim FeBr3}C_{8}H_{7}Br_{3}$
$Z\quad\quad Z\quad\quad\quad Z\quad\quad Z$
On obtient un système
$\begin{array}{rcl} \left\lbrace\begin{array}{rcl} x+y+z&=&n_{Br_{2}}\\ x+y&=&n_{AgBr} \end{array}\right.\\&\text{avec }&n_{Br_{2}}\\&=&\dfrac{\mu_{Br_{2}}\times V_{Br_{2}}}{2M_{Br}}\\&=&\dfrac{3250 \times 8.4\cdot 10^{-3}}{2\times 80}\\&=&0.17\,mol\\&\text{et }n_{AgBr}\\&=&\dfrac{19.1}{108+80}\\&=&0.10\,mol\\&\Rightarrow&\left\lbrace\begin{array}{rcl} x+y+z&=&0.17\\ x+y&=&0.10 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{rcl} x+2y&=&0.17\quad (1)\\ x+y&=&0.10\quad (2) \end{array}\right.\\&\Rightarrow&(1)-(2)\\&\Rightarrow&y\\&=&0.17\,mol\left\lbrace\begin{array}{rcl} y&=&0.07\\ x&=&0.03\,mol \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{rcl} n_{C_{6}H_{6}}&=&0.03\,mol\\ n_{C_{8}H_{8}}&=&0.07\,mol \end{array}\right. \end{array}$
c. Détermination de la masse volumique du styrène
$\begin{array}{rcl} V_{b}&=&\dfrac{n_{C_{6}H_{6}}\times M_{C_{6}H_{6}}}{\mu_{b}}\\&=&\dfrac{0.05\times 78}{0.880}\\&\Rightarrow&V_{b}\\&=&4.4\,mL V_{b}+V_{C_{8}H_{8}}\\&=&V\\&\Rightarrow&V_{C_{8}H_{8}}\\&=&V-V_{b}\\&=&10-4.4\\&\Rightarrow&V_{C_{8}H_{8}}\\&=&5.6\,mL \end{array}$
$\begin{array}{rcl} \mu_{C_{8}H_{8}}&=&\dfrac{m_{C_{8}H_{8}}}{V_{C_{8}H_{8}}}\\&=&\dfrac{n_{C_{8}H_{8}}\times M_{C_{8}H_{8}}}{V_{C_{8}H_{8}}}\\&=&\dfrac{0.12\times 104}{5.6}\\&\Rightarrow&\mu_{C_{8}H_{8}}\\&=&18.6\,g\,mL^{-1} \end{array}$
Exercice 3
1. Nombre d'isomères du dimêthylbenzène et leur nom
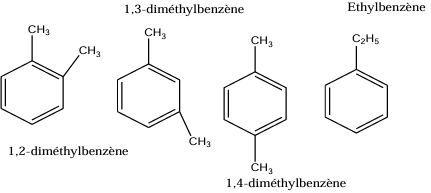
2. Les formules semi-développées des deux produits que l'on obtient?
$CH_{2}Cl-CH_{2}-CH_{3}$ et
$CH_{3}-CHCl-CH_{3}$
Nom systématique du produit le plus symétrique
$CH_{3}-CHCl-CH_{3}$ :$2-$ chloropropane
3. Nombre d'insomères qu'on peut obtenir
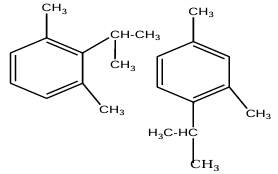
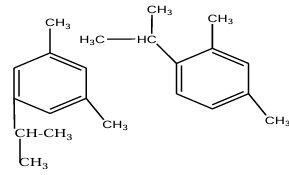
Soit quatre isomères
Compte tenu de l'encombrement" du groupe isopropyle, l'isomère qui sera le plus abondant le $3-$isopropylemétaxylène :
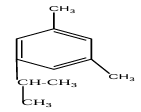
4. Détermination de sa formule brute d sa masse molaire et de sa formule semi-développée.
Soit $C_{11}H_{16-x}\left(NO_{2}\right)_{2}$ la formule brute du composé
$\begin{array}{rcl} \dfrac{12\times 11}{\%C}&=&\dfrac{116-x}{\%H}\\&=&\dfrac{32x}{\%O}\\&=&\dfrac{14x}{\%N}\\&=&\dfrac{M}{100}\\&=&\dfrac{12x11+16-x+32x+14x}{100} \end{array}$
$\begin{array}{rcl} 132+16-x+32x+14x&=&\dfrac{12\times 111\times 100}{46.6}\\&\Rightarrow&145x\\&=&283.3-148\\&\Rightarrow&x\\&=&\dfrac{135.3}{45}\\&=&3\\&\Rightarrow&C_{11}H_{13}\left(NO_{2}\right)_{3} \end{array}$
$\begin{array}{rcl} \dfrac{M}{100}&=&\dfrac{12\times 11}{\%C}\\&\Rightarrow&M\\&=&\dfrac{12\times 11\times 100}{46.6}\\&\Rightarrow&M\\&=&283.3\,g\,mol^{-1} \end{array}$
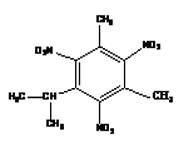
Exercice 4
1. Formules semi-développées du toluène et de $T.N.T$
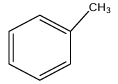
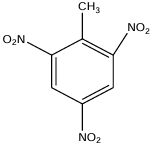
Nom systématique du toluène : méthylbenzène
2.a. Équation bilan de la réaction.
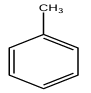
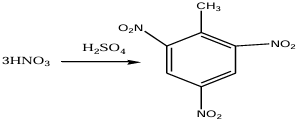
La réaction est une réaction de substitution ?
b. Calcul de la masse de toluène nécessaire à la synthèse de une tonne de $T.N.T$
D'après le bilan molaire :
$\begin{array}{rcl} n_{TNT}&=&n_{\text{toluène}}\\&\Rightarrow&\dfrac{m_{TNT}}{M_{TNT}}\\&=&\dfrac{m_{\text{toluène}}}{M_{\text{toluène}}}\\&\Rightarrow&m_{TNT}\\&=&\dfrac{m_{\text{toluène}}\times M_{TNT}}{M_{\text{Toluène}}}\\&=&\dfrac{1\times 208}{92}\\&\Rightarrow&m_{TNT}\\&=&2.26\,t \end{array}$
c. Équation bilan de la réaction d'explosion
$\begin{array}{rcl} C_{7}H_{5}N_{3}O_{6}&\longrightarrow& \dfrac{7}{2}CO+\dfrac{7}{2}C+\dfrac{5}{2}H_{2}O+\dfrac{3}{2}N_{2}\\&\text{ ou }&2C_{7}H_{5}N_{3}O_{6}\\&\longrightarrow&7CO+7C+5H_{2}O+3N_{2} \end{array}$
Calcul de la masse de carbone produit par l'explosion de $100$ de $T.N.T$
D'après le bilan molaire :
$\begin{array}{rcl} \dfrac{n_{c}}{7}&=&\dfrac{n_{TNT}}{2}\\&\Rightarrow&\dfrac{m_{c}}{7M_{c}}\\&=&\dfrac{m_{TNT}}{2M_{TNT}}\\&\Rightarrow&m_{c}\\&=&\dfrac{7m_{TNT}\times M_{c}}{2M_{TNT}}\\&=&\dfrac{7\times 100\times 12}{2\times 208}\\&\Rightarrow&m_{c}\\&=&20.5\,t \end{array}$
3.a. On observe un $pH$ acide
b. Formule semi-développée et nom du composé organique formé dans le flacon $F_{2}$
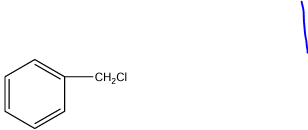
Un composé est un composé aromatique car il contient un noyau benzénique
c. Formules semi-développées et nom des trois composés chlorés
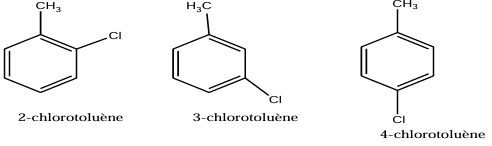
Exercice 5
1. Déduisons le produit est un composé aromatique
Par hydrogénation de $A$, en présence d'un catalyseur on obtient $C_{8}H_{16}$ , le composé contient trois insaturations
En présence de brome, et avec du fer, $A$ donne un produit de substitution, il s'agit d'une substitution d'un noyau aromatique
Montrons que l'action du brome est une monosubstitution
En présence de brome, et avec du fer, $A$ donne un produit de substitution, il s'agit d'une substitution d'un noyau aromatique
Montrons que l'action du brome est une monosubstitution
Soit $C_{8}H_{10-x}Br_{x}$ le produit
$\begin{array}{rcl} \dfrac{xM_{Br}}{Br}&=&\dfrac{M_{C_{8}H_{10-x}Br_{x}}}{100}\\&\Rightarrow&\dfrac{80x}{43}\\&=&\dfrac{106-x+80x}{100}\\&\Rightarrow&80\times 100\\&=&43(106+79x)\\&\Rightarrow&8000x\\&=&4558+3397x\\&\Rightarrow&4603x\\&=&4558\\&\Rightarrow&x\\&=&\dfrac{4558}{4603}\\&\Rightarrow&x\\&=&1\\&\Rightarrow&C_{8}H_{8}Br \end{array}$
Il s'agit d'une monosubstitution
2. Proposer les différentes formules développées et noms de $A$
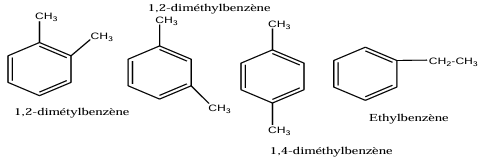
3. Précisons la formule de $B$
Une déshydrogénation de $A$ donne $B$ de formule brute $C_{8}H_{8}$ ; et que $B$ décolore l'eau de brome.
$B$ possède la fonction alcène $B$ est le styrène de formule :
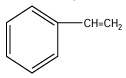
4. Précisons la formule de $A$
$A$ est éthylbenzène de formule :
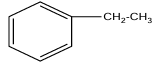
5. Il existe trois dérivés monobromés de $A$
Formules semi-développées des dérivés monobromés de $A$

Exercice 6
1. Équation-bilan de la réaction.
$C_{6}H_{6}+3HNO_{3}\longrightarrow^{\lim\limits H_{2}SO_{4}}C_{6}H_{3}\left(NO_{2}\right)_{3}+3H_{2}O$
2. Expression de la masse de toluène théorique
$\begin{array}{rcl} r&=&\dfrac{m_{ex}}{m_{th}}\\&\Rightarrow&m_{th}\\&=&\dfrac{m_{ex}}{r} \end{array}$
D'après le bilan molaire
$\begin{array}{rcl} n_{C_{6}H_{6}}&=&n_{th}\\&\Rightarrow&\dfrac{m_{C_{6}H_{6}}}{M_{C_{6}H_{6}}}\\&=&\dfrac{m_{th}}{M_{th}}\\&\Rightarrow&m_{C_{6}H_{6}}\\&=&\dfrac{m_{th}\times M_{C_{6}H_{6}}}{M_{th}}\\&=&\dfrac{m_{ex}\times M_{C_{6}H_{6}}}{rM_{th}}\\&=&\dfrac{1\times 78}{0.90\times 213}\\&\Rightarrow&m_{C_{6}H_{6}}\\&=&0.41\,kg \end{array}$
Exercice 7
1. Formule brute de $A$
Soit $C_{6}H_{6-x}\left(C_{2}H_{5}\right)_{x}$ la formule brute du composé
$\begin{array}{rcl} \dfrac{12\times 6+112\times 2x}{\%C}&=&\dfrac{1\times 6-x+5x}{\%H}\\&\Rightarrow&9.4\times (72+24x)\\&=&90.6\times (6+4x)\\&\Rightarrow&676.8+225.6x\\&=&543.6+362.4x\\&\Rightarrow&362.4x-225.6x\\&=&676.8-543.6\\&\Rightarrow&136.8x\\&=&133.2\\&\Rightarrow&x\\&=&\dfrac{133.2}{136.8}\\&\Rightarrow&x\\&=&1 \end{array}$
Équation-bilan de la réaction
$C_{6}H_{6}+C_{2}H_{5}-CI\longrightarrow^{\lim\limits A1C1_{3}}C_{6}H_{6}-C_{2}H_{5}+HCI$
La formule développée de $A$ est :
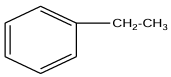
2. Formule développée de $B$
$C_{6}H_{5}-C_{2}H_{5}=C_{8}H_{10}$
Soit $C_{8}H_{10-x}$ la formule brute du composé $B$
$\begin{array}{rcl} \dfrac{12\times 8}{\%C}&=&\dfrac{11\times 10-x}{\%H}\\&\Rightarrow&\%H\times 12\times 8\\&=&\%C(10-x)\\&\Rightarrow&7.7\times 12\times 8\\&=&92.3\times (10-x)\\&\Rightarrow&739.2\\&=&923-92.3x\\&\Rightarrow&92.3x\\&=&923-739.2\\&\Rightarrow&92.3x\\&=&183.8\\&\Rightarrow&x\\&=&\dfrac{183.8}{92.3}\\&\Rightarrow&x\\&=&2\\&\Rightarrow&C_{8}H_{8}\\&\Rightarrow& \end{array}$
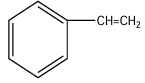
3. Le motif du polymère obtenu est $-\left(CH\left(C_{6}H_{5}\right)-CH_{2}\right)-$
Exercice 8
1. Écrivons et complétons la réaction suivante en précisant le catalyseur :
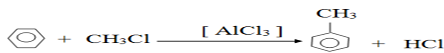
2. Volume d'air nécessaire pour la combustion
Équation de la combustion
$C_{7}H_{8}+9O_{2}\longrightarrow 7CO_{2}+4H_{2}O$
$\begin{array}{rcl} PV_{o_{2}}&=&n_{o_{2}}RT\\&\Rightarrow&V_{o_{2}}\\&=&\dfrac{n_{o_{2}}RT}{P}\\&\text{ or }n_{o_{2}}\\&=&9n_{\text{Toluène}}\\&=&\dfrac{9m_{\text{toluène}}}{M_{\text{Toluène}}}\\&\text{ et }V_{\text{Air}}\\&=&5V_{o_{2}}\\&\Rightarrow&V_{\text{Air}}\\&=&5\dfrac{9m_{\text{Toluène}}RT}{M_{\text{Toluène}}P}\\&\Rightarrow&V_{\text{Air}}\\&=&5\times\dfrac{9\times 136\times 8.31\times (273+27)}{92\times 11.013\cdot 10^{5}}\\&\Rightarrow&V_{\text{Air}}\\&=&1.6\,L \end{array}$
Exercice 9
1. Écriture des deux réactions qui permettent d'aboutir au produit.
$C_{6}H_{6}+Br_{2}\longrightarrow^{\lim\limits FeBr_{3}}C_{6}H_{6}Br+HBr$
$C_{6}H_{6}Br+Br_{2}\longrightarrow^{\lim\limits FeBr_{3}}C_{6}H_{6}Br_{2}+HBr$
Précisons les conditions expérimentales.
Il faut la présence d'un catalyseur comme $FeBr_{2}$ et la présence d'un stabilisateur comme le tétrachlorure de carbone $CCl_{4}$
2. Calcul :
2.1. De la masse de benzène nécessaire.
D'après le bilan molaire :
$C_{6}H_{6}+Br_{2}\longrightarrow^{\lim\limits FeBr_{3}}C_{2}H_{6}Br+Br+HBr$
$C_{6}H_{6}Br+Br_{2}\longrightarrow^{\lim\limits FeBr_{3}}C_{6}H_{6}Br_{2}+HBr$

Ajouter un commentaire