Ondes progressives, interférences mécaniques - 1er s

 

 

I. Onde 

 

1. Ébranlement

 

1.1. Exemple d'un signal mécanique non entretenu

 

Une corde élastique $AB$ est tendue. 

 

On veut envoyer un message de Avers $B.$

 

Pour cela, on soulève et descend rapidement l'extrémité $A$, puis on la ramène à sa position initiale. 

 

Après un certain intervalle de temps, la personne en $B$ ressent la secousse produite en A (schéma ci-dessous)

 

 

On dit qu'un signal s'est propagé le long de la corde.

 

La corde qui permet de transmettre le signal constitue le milieu de propagation.

 

La personne en $A$ qui crée le signal s'appelle l' émetteur ou la source.

 

La personne en $B$ est le récepteur ou le détecteur du signal.

 

La direction et le sens dans lesquels le signal se déplace constituent la direction et le sens de propagation

 

1.3. Conclusions

 

$\surd\ $Un ébranlement  est une déformation locale et brève dans un milieu élastique.

 

On distingue trois types d'ébranlement :

 

$-\ $un ébranlement transversal : si le déplacement des points du milieu de propagation est perpendiculaire à la direction de propagation.

 

 

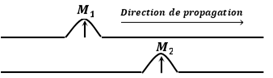
$-\ $Un ébranlement longitudinal : si le déplacement des points du milieu de propagation est parallèle à la direction de propagation.

 

 

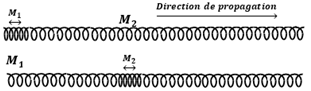
$-\ $Un milieu élastique  est un milieu capable de se déformé et de revenir à son état initial quand on cesse la déformation.

 

2. Définition de l'onde

 

On appelle onde, le phénomène résultant de la propagation d'une succession d'ébranlements dans un milieu donné sans transport de matière, mais avec d'énergie.

 

3. Propriétés des ondes 

 

3.1. La direction de propagation 

 

Une onde se propage, à partir de la source, dans toutes les directions qui lui sont offertes

 

3.1.1. Onde à une dimension

 

La propagation a lieu selon une seule direction (mais éventuellement dans les deux sens). 

 

C'est le cas, par exemple, de l'onde se propageant le long d'une corde.

 

3.1.2. Onde à deux dimensions

 

La propagation a lieu dans un plan. 

 

C'est le cas de l'onde qui est engendrée à la surface de l'eau lorsqu'on y jette un caillou

 

3.1.3. Onde à trois dimensions 

 

La propagation a lieu dans toutes les directions de l'espace. 

 

C'est le cas des ondes sonores (ou acoustiques).

 

3.2. Onde transversale et onde longitudinale.

 

Une onde mécanique progressive est dite transversale si le déplacement des points du milieu de propagation atteints par la perturbation est perpendiculaire à la direction de propagation.

 

Une onde mécanique progressive est dite longitudinale si le déplacement des points du milieu de propagation atteints par la perturbation est parallèle à la direction de propagation

 

 

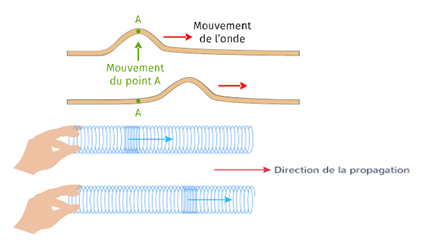
$-\ $Onde de torsion

 

3.3. Célérité d'une onde mécanique :

 

3.3.1. Définition 

 

On appelle célérité $v$ d'un ébranlement, la vitesse de propagation de l'ébranlement. 

 

C'est le quotient de la distance $d$ parcourue par l'ébranlement par la durée $\Delta t$ du parcours.    

$$\boxed{v=\dfrac{d}{\Delta t}}\quad\left\lbrace\begin{array}{lcl} d&:&\text{en }m\\ \Delta t&:&\text{en }s\\ v&:&\text{en }m\cdot s^{-1} \end{array}\right.$$

$$\begin{array}{|l|l|l|l|l|} \hline \text{Onde}&\text{Son}&\text{Son}&\text{Sismique}&\text{Vague}\\ \hline \text{Milieu de propagation}&\text{Air}&\text{Eau}&\text{Terre/Roche}&\text{Eau}\\ \hline \text{Vitesse }\left(\text{en }m\cdot s^{-1}\right)&340&1500&1500\text{ à }5000&0.1\text{ à }1\text{ voire plus}\\ \hline \end{array}$$

 

3.3.2. Facteurs influençant la célérité 

 

La célérité d'une onde ne dépend que du milieu et jamais de l'amplitude de l'onde.

 

$\ast\ $La célérité de l'onde le long d'une corde dépend :

 

$-\ $La tension : lorsque la tension de la corde augmente, la vitesse de propagation ou la célérité augmente.

 

$-\ $La masse linéique : lorsque la masse de la corde est faible (la masse linéique diminue), la vitesse diminue. 

 

$-\ $La célérité de l'onde dépend de la tension $F$ de la corde et de la masse linéique $($masse par unité de longueur $\mu=m/L)$ de la corde.$$\boxed{v=\sqrt{\dfrac{F}{\mu}}}$$

 

$\ast\ $La célérité du son dépend du milieu de propagation. 

 

Elle est plus importante dans les solides et les liquides que dans les gaz comme l'air.

 

La célérité d'un ébranlement dépend de la nature du milieu matériel dans lequel il se propage et de ses propriétés.

 

3.4. Retard lors de la propagation d'une onde 

 

Soit $M_{1}$ et $M_{2}$ deux points distincts du milieu de propagation.

 

La perturbation passe d'abord en $M_{1}$ à l'instant $t_{1}$ puis en $M_{2}$ à l'instant $t_{2}$

 

La durée de propagation de la perturbation entre $M_{1}$ et $M_{2}$ est le retard notée $\tau$

 

 

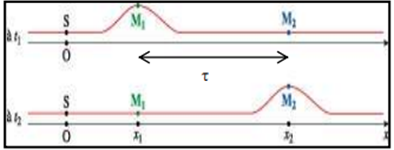
Donc : $\tau=t_{2}-t_{1}$  ou $\boxed{\tau=\dfrac{M_{1}M_{2}}{v}}$ ; $M_{1}M_{2}$ distance entre  deux points du milieu de propagation et $v$ la célérité de l'onde. 

 

Le temps nécessaire pour qu'une onde de célérité $v$ se propage d'un point $A$ à un point $B$ dans un milieu est appelé retard (ou temps de propagation) de l'onde :

 

3. Principe de propagation 

 

 

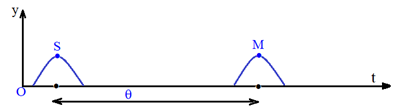
Chaque point $M$ du milieu propagateur reproduit le même mouvement que la source $S$ mais avec un retard de temps $\theta.$

 

$\theta$ : est le temps nécessaire pour que l'ébranlement passe de $S$ à $M.$

 

$V=\dfrac{SM}{\theta}$, la distance $SM$ pris lorsque la corde est au repos. 

 

On pose $SM=x$ donc $\theta=\dfrac{x}{v}$

 

À $t=0$, $S$ est en mouvement et $M$ au repos.

 

À $t=t+\theta$, $S$ au repos et $M$ en mouvement.