Mouvement de chute verticale d'un solide - Ts

 

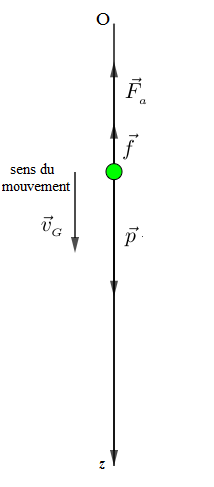
Une bille de masse $m$ est abandonnée sans vitesse initiale dans un fluide de masse volumique $\rho.$

 

Donner l'expression de la vitesse de la bille sachant que les seules forces appliquées au centre d'inertie $G$ de ce solide sont : le poids $\vec{p}$, la poussée d'Archimède $\vec{F}_{_{a}}$ et les forces de frottement fluide $\vec{f}.$

$\centerdot\ \ $ Le système étudié est la bille, considérée comme un solide ou un point matériel.

 

$\centerdot\ \ $ Le référentiel d'étude est le référentiel terrestre supposé galiléen.

 

$\centerdot\ \ $ Les forces extérieures appliquées au système sont :

 

$-\ \ $ Le poids $\vec{p}=m.\vec{g}$ ; force exercée par la terre sur la bille.

 

$-\ \ $ La poussée d'Archimède ; force exercée par le fluide sur la bille, notée $\vec{F}_{_{a}}=-\rho.V.\vec{g}$ où $V$ est le volume de fluide déplacé lors de l'immersion, équivalent au volume de la partie du solide immergée.

 

$-\ \ $ Les forces de frottement fluide ; $\vec{f}=-k.\vec{v}_{_{G}}$ pour des vitesses faibles, toujours colinéaires et opposées au sens du mouvement avec $k$ coefficient de frottement dépendant du fluide et de la forme du solide.

 

Remarque

 

Dans le cas des vitesses plus élevées, $\vec{f}=-k.v_{_{G}}^{2}.\vec{j}\ $ où $\ \vec{j}$ est un vecteur unitaire orienté dans le sens du mouvement.

$\centerdot\ \ $ Appliquons la deuxième loi de Newton. On obtient alors : $$\sum {\overrightarrow{F}}_{\text{ext}}=m.{\overrightarrow{a}}_{{}_G}$$

 

D'où, $$\overrightarrow{p}+\overrightarrow{f}+{\overrightarrow{F}}_{{}_a}=m.{\overrightarrow{a}}_{{}_G}$$

 

Soit : $$m.\overrightarrow{g}-k.{\overrightarrow{v}}_{{}_G}-\rho .V.\overrightarrow{g}=m.{\overrightarrow{a}}_{{}_G}$$

 

$\centerdot\ \ $ Choisissons comme repère de projection l'axe $Oz$ vertical orienté vers le bas.

 

$\centerdot\ \ $ Projetons cette dernière relation vectorielle suivant l'axe du repère. On obtient alors : $$m.g-k.v_{{}_G}-\rho .V.g=m.a_{{}_G}$$

 

Comme $a_{_{G}}=\dfrac{\mathrm{d}v_{_{G}}}{\mathrm{d}t}$ alors, la relation devient : $$m.g-k.v_{{}_G}-\rho .V.g=m.{\displaystyle \frac{\mathrm{d}{v}_{{}_G}}{\mathrm{d}t}}$$

 

Soit : $$\boxed{{\displaystyle {\displaystyle \frac{\mathrm{d}{v}_{{}_G}}{\mathrm{d}t}}+{\displaystyle \frac{k}{m}}{v}_{{}_G}={\displaystyle \frac{g}{m}}(m-\rho .V)}}$$

 

On reconnait alors l'équation différentielle d'ordre 1 à coefficients constants en $v_{_{G}}.$

 

Cours mathématiques : Cette équation différentielle, de la forme $ay'+by=c$ avec $a=1\;,\ b=\dfrac{k}{m}\ $ et $\ c=\dfrac{g}{m}\left(m-\rho.V\right)$, a pour solution : $$y(t)=f_2(t)+f_1(t)$$ avec $f_{2}(t)$ solution générale de l'équation $ay'+by=0\ $ et $\ f_{1}(t)$ une solution particulière de l'équation $ay'+by=c.$

 

Par suite,  $$f_2(t)=\lambda {\mathrm{e}}^{-bt}\text{ et }{f}_1(t)={\displaystyle \frac{c}{b}}$$ 

 

D'où, $$v_{{}_G}(t)=\lambda {\mathrm{e}}^{-\frac{kt}{m}}+{\displaystyle \frac{g}{k}}(m-\rho .V)$$

 

Or, à $t=0\;,\ v_{0}=0\ $ donc, $\ \lambda\mathrm{e}^{0}+\dfrac{g}{k}\left(m-\rho.V\right)=0.$ 

 

Ce qui donne : $\lambda=-\dfrac{g}{k}\left(m-\rho.V\right)$ 

 

Et par conséquent, $$\boxed{{\displaystyle v_{{}_G}(t)={\displaystyle \frac{g}{k}}(m-\rho .V)(1-{\mathrm{e}}^{-\frac{kt}{m}})}}$$

La vitesse limite $v_{_{\text{lim}}}$ est la vitesse maximale atteinte par la bille lors de sa chute dans le fluide.

 

Cette vitesse est atteinte quand l'accélération s'annule ; c'est-à-dire la vitesse est une constante et donc $\dfrac{\mathrm{d}v_{_{G}}}{\mathrm{d}t}=0$

 

On a : $\ \dfrac{\mathrm{d}v_{_{G}}}{\mathrm{d}t}+\dfrac{k}{m}v_{_{G}}=\dfrac{g}{m}\left(m-\rho.V\right)\ $ or, $\ \dfrac{\mathrm{d}v_{_{G}}}{\mathrm{d}t}=0$

 

Donc, $$\boxed{{\displaystyle v_{{}_{\text{lim}}}={\displaystyle \frac{g}{k}}(m-\rho .V)}}$$

C'est un indicateur qui informe sur la durée pour atteindre la vitesse limite. $$\boxed{{\displaystyle \tau ={\displaystyle \frac{m}{k}}}}$$

 

Remarque 

 

A la date $t=\tau\;,\ v_{_{G}}=0.63v_{_{\text{lim}}}$ et au bout de $t=5\tau$, le régime permanent est atteint ; le mouvement est alors rectiligne uniforme. 

Un solide est en chute libre (sans frottement) si le poids est la seule force extérieure appliquée.

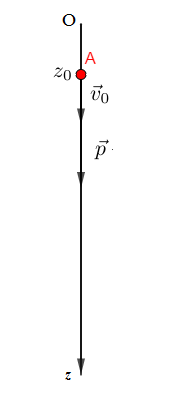
A partir d'un point $A$ situé au dessus du sol, une bille de masse $m$ est lâchée à $t_{0}=0$, avec une vitesse initiale $\vec{v}_{0}.$

 

Les frottements de l'air étant négligeables, déterminer alors les équations du mouvement.

La bille étant en mouvement de chute libre, on se place alors dans le repère terrestre considéré comme galiléen.

 

Le système étudié est la bille, considérée comme un point matériel.

 

Le poids $\vec{p}=m.\vec{g}$ est la seule force extérieure appliquée au système.

Ainsi, en appliquant le théorème du centre d'inertie, on a : $$\overrightarrow{p}=m.{\overrightarrow{a}}_{{}_G}$$

 

D'où, $$m.\overrightarrow{g}=m.{\overrightarrow{a}}_{{}_G}$$

 

Soit : $$\overrightarrow{g}={\overrightarrow{a}}_{{}_G}$$

 

Projetons cette dernière relation vectorielle suivant un axe vertical orienté vers le bas. On obtient alors : $$g=a_{{}_G}$$

 

Comme $a_{_{G}}=\dfrac{\mathrm{d}v_{_{G}}}{\mathrm{d}t}=g$ alors, par intégration, on obtient : $$\boxed{{\displaystyle v_{{}_G}=gt+v_0}}$$

 

De même, $v_{_{G}}=\dfrac{\mathrm{d}z}{\mathrm{d}t}$ d'où, par intégration, on obtient l'équation horaire du mouvement donnée par : $$\boxed{{\displaystyle z={\displaystyle \frac{1}{2}}g{t}^2+v_{0}t+z_0}}$$

 

Remarque

 

Le mouvement est rectiligne uniformément varié.