Induction magnétique-étude d'un dipôle (R, L)
Classe:
Terminale
Un conducteur électrique, parcouru un courant et plongé dans un champ magnétique, pouvait se mettre en mouvement sous l'effet de la force de Laplace. Réciproquement, le mouvement d'un circuit électrique dans un champ magnétique provoque l'apparition d'un courant induit dans le circuit. C'est le phénomène d'induction électromagnétique, qui est à la base de l'électricité moderne
I. Induction électromagnétique
1. Notion de flux magnétique
1.1. Vecteur surface : orientation d'un circuit
Soit un contour plan $(C)$ situé dans une région où un champ magnétique de vecteur $\overrightarrow{B}.$ Ce contour $t$ orienté arbitrairement limite sur une surface plane.
Le vecteur $\overrightarrow{S}$ est défini comme suit :
$-\ $il est orthogonal au plan du contour ;
$-\ $son sens est donné par la règle de la main droite : la main droite empoigne le contour dans le sens positif choisi ; le pouce écarté des autres doigts donne le sens du vecteur unitaire $\overrightarrow{n}$ associé à la surface : $$\overrightarrow{S}=S\overrightarrow{n}$$
Exemples d'orientation de circuits
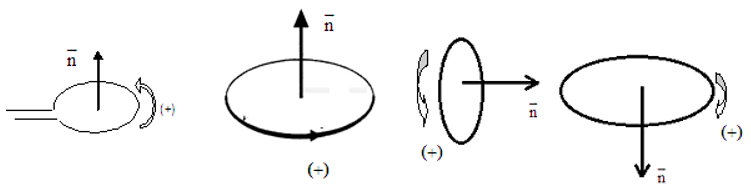
1.2. Expression du flux magnétique
Le flux magnétique est une grandeur mesurable caractérisant l'intensité et la répartition du champ magnétique.
Le flux $\phi$ du champ magnétique à travers le contour limitant une surface $S$ a pour expression :
$$\phi=\overrightarrow{B}\cdot\overrightarrow{S}=\overrightarrow{B}\cdot \overrightarrow{n}S\\\Rightarrow\phi=BS\cos(\overrightarrow{n}\;,\ \overrightarrow{B})$$
$S$ en mètres $(m)$
$B$ en teslas $(T)$
$\phi$ en webers $(Wb)$
Pour un circuit comportant $N$ spires $\phi=NBS\cos(\overrightarrow{n}\;,\ \overrightarrow{B})$
2. Mise en évidence du phénomène d'induction
2.1. Expérience
Réalisons une série d'expériences à l'aide d'une bobine liée à un microampèremètre et d'un aimant droit

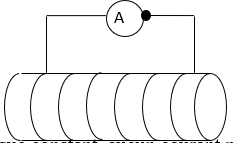
L'expérience montre que :
$-\ $tant que la bobine est immobile dans le champ magnétique constant, aucun courant ne circule
$-\ $la bobine déformée ou déplacée dans le champ magnétique, le microampèremètre indique le passage du courant
$-\ $le microampèremètre indique le passage d'un courant dans la bobine lorsque celle-ci est plongée dans un champ magnétique variable ou en faisant tourner la bobine sans la déformer
2.2. Interprétation
Alors que le circuit de la bobine ne comporte aucun générateur, un courant, donc circulation d'électrons, est crée : il apparait une force électromotrice $(f.é.m.)$
Toute variation du flux du champ magnétique dans la bobine provoque ce phénomène appelé phénomène d'induction électromagnétique. Le courant crée est appelé courant induit. La source du champ magnétique est l'inducteur ou circuit inducteur. La bobine qui est le siège du courant est l'induit ou circuit induit.
Remarque :
La force électromotrice $(f.é.m.)$, qui ne dure que tant que dure la variation du flux magnétique, se manifeste par :
$-\ $une tension aux bornes du circuit si ce circuit est ouvert ;
$-\ $la circulation d'un courant dans ce circuit, ce circuit est fermé
3. Sens du courant induit : loi de Lenz
3.1. Expérience
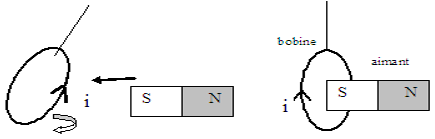
Lorsqu'on approche le pôle sud de l'aimant, par exemple, d'une face de la bobine, le sens du courant induit est tel que cette face devient face sud ; la bobine tente de repousser l'aimant.
Si l'on éloigne le pôle sud de l'aimant de la même face, le courant induit change de sens, la face sud de la bobine devient alors face nord et la bobine tente de retenir l'aimant.
3.2. Énoncé de loi de Lenz
Toute variation du flux magnétique à travers un circuit entraine la circulation d'un courant induit.
Le sens du courant est telque, par ses effets électromagnétiques, il s'oppose toujours à la cause qui lui a donné naissance.
4. Loi de Lenz-Faraday : $f.é.m.$
4.1. Expression de la $f.é.m.$ induite
Le circuit (l'induit), siège d'un flux magnétique variable, se comporte comme un générateur.
Il possède alors une $f.é.m.$ ; la loi de Lenz-Faraday permet d'exprimer la $f.é.m$ induite suivant l'expression :
$$e=-\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}$$
$e$ en volts $(V)$
$\Phi$ en webers $(Wb)$
$t$ en secondes $(s)$
Remarque :
Si le flux magnétique varie $\Delta\Phi$ pendant l'intervalle de temps $\Delta t$, on définit une $f.é.m$ moyenne
$$e=-\dfrac{\Delta\Phi}{\Delta t}$$
4.2. Sens du courant induit
Le circuit ayant été orienté, on peut facilement prévoir le sens du courant induit prévoir le sens du courant induit
$\bullet\ $Si $\Delta\Phi$ est positif $e$ est négatif : si le circuit est fermé, le courant circule dans le sens négatif.
$\bullet\ $Si $\Delta\Phi$ est négatif $e$ est positif : si le circuit est fermé, le courant circule dans le sens positif.
4.5. Intensité du courant induit
Si $R$ est la résistance totale du circuit induit, l'intensité du courant induit est donnée par la loi de Pouillet
$$i=\dfrac{e}{R}$$
$e$ en $(V)$
$i$ en $(A)$
$R$ en ohm $(\Omega)$
5. Applications de l'induction
Les applications de phénomène d'induction électromagnétiques sont très nombres Ce sont essentiellement :
5.1. Les alternateurs
Les alternateurs sont des générateurs de courants (tension) alternatifs. Ils transforment une énergie mécanique (rotation d'une turbine) en travail électrique (électricité)

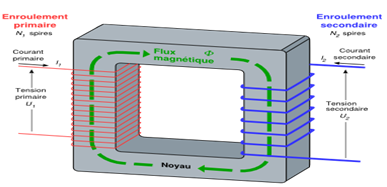
5.2. Les transformateurs
Ils sont pour but de transférer l'énergie d'une bobine primaire à une bobine secondaire en faisant varier les grandeurs électriques

Lorsque le transformateur est en fonctionnement (idéal), des courants sinusoïdaux d'intensité $i_{1}$ et $i_{2}$ $($de valeurs maximales $I_{1}$ et $I_{2})$ passent dans le primaire et le secondaire.
Le rendement des transformateurs est excellent et dépasse $99\%.$ Ainsi, si on néglige les pertes, la puissance est transmise intégralement, $U_{2}\cdot I_{2}=U_{1}\cdot I_{1}$
Les grandeurs précédentes sont alors liées par le rapport de transformation :
$$r=\dfrac{U_{2}}{U_{1}}\approx\dfrac{I_{1}}{I_{2}}\approx\dfrac{N_{2}}{N_{1}}$$
5.3. Courants de Foucault
Ce sont des courants induits qui apparaissent dans des conducteurs lors des variations de flux magnétique.
$-\ $Inconvénients
Les courants de Foucault prennent naissance dans les carcasses métalliques des moteurs, des transformateurs, des alternateurs... L'échauffement par effet joule qui en résulte constitue une perte d'énergie, ce qui diminue le rendement de ces appareils.
$-\ $Avantages
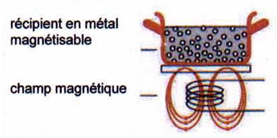
$\bullet\ $Plaque à induction
Une plaque à induction produit un champ magnétique sinusoïdal à $50\,kHz.$ Ce champ induit des courants de Foucault dans la casserole (surtout le fond). Le fond de la casserole doit être suffisamment résistif pour que le courant induit génère de la chaleur par effet joule ce qui chauffe le contenu

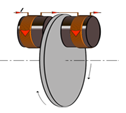
$\bullet\ $Freinage
Lorsque le chauffeur de camion appuie sur la pédale de frein, il alimente en courant les bobines des électroaimants. Le flux variable résultant, traverse le disque dans lequel apparaît des courants de Foucault induits. Ces courants génèrent des forces de Laplace qui s'opposent à la rotation du disque et freinent le camion

II. Auto-induction
Toute variation de flux magnétique à proximité d’un conducteur fait apparaitre une $f.é.m.$ d'induction aux bornes du conducteur ou un courant induit si le circuit est fermé. On distingue alors clairement un inducteur, source du champ magnétique « (aimant, bobine...) et un induit, siège du phénomène d'induction. Mais, une bobine parcourue par un courant crée son propre champ magnétique. Si celui-ci varie, elle provoque des phénomènes d'induction appelées ici auto-induction car l'inducteur et l'induit sont confondus.
1. Mise en évidence du phénomène d'auto-induction

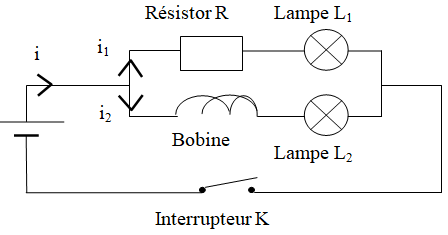
Le montage réalisé ci-dessus comporte deux lampes toutes identiques. Le résistor et la bobine possèdent la même résistance.
$\bullet\ $On ferme l'interrupteur $K.$ La lampe $L_{1}$ brille instantanément tandis que la lampe $L_{2}$ s'allume progressivement : le courant $i_{1}$ s'établit donc instantanément mais $i_{2}$ ne s'établit que progressivement
$\bullet\ $ On ouvre l'interrupteur $K.$ La lampe $L_{1}$ s'éteint instantanément tandis que la lampe $L_{2}$ s'éteint progressivement : le courant $i_{1}$ s'annule donc instantanément mais $i_{2}$ ne s'annule que progressivement
$\bullet\ $La bobine tend donc à s'opposer à l'établissement ou à la rupture du courant dans sa branche
2. Interprétation
Lorsqu'on ferme l'interrupteur, la variation du flux propre dans la bobine crée une $f.é.m$ d'induction qui s'oppose à l'établissement.
Dans le cas de l'ouverture du circuit, la $f.é.m.$ d'induction s'oppose à la disparition du courant
Remarque :
C'est le phénomène d'auto-induction qui explique l'étincelle de rupture lorsqu'on débranche brusquement des appareils contenant des moteurs en fonctionnement
3. Inductance
3.1. Flux propre
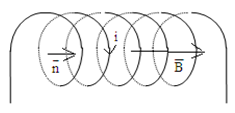
Soit un solénoïde, de section $S$, de longueur $l$ grande devant son rayon, comportant $N$ spires et parcouru par un courant $i$
Orientons arbitrairement le circuit

$\Phi=N\overrightarrow{B}\cdot\overrightarrow{S}=N\overrightarrow{B}\cdot\overrightarrow{n}S$
$\Rightarrow\Phi=NBS\quad\text{où}\quad B=\dfrac{\mu_{0}Ni}{l}$
$\Rightarrow\Phi=N\dfrac{\mu_{0}Ni}{l}S$
$\Rightarrow\Phi=\dfrac{\mu_{0}Ni}{l}S$
3.2. Inductance d'un solénoïde
La valeur instantanée de flux propre est donc proportionnelle à l'intensité instantanée
$$\Phi=Li\quad\text{en posant}\quad L=\dfrac{\mu_{0}N^{2}S}{l}$$
On constate $L$ ne dépend que de la constitution du solénoïde.
$L$ est l'inductance ou auto-inductance du solénoïde. L'inductance $L$ d'une portion de circuit (bobine) correspond au coefficient de proportionnalité entre son flux propre et l'intensité du courant qui la traverse. Il mesure en quelque sorte, l' « efficacité d'une bobine à créer un flux magnétique (donc un champ magnétique) pour une intensité donnée Dans le $S.I$ l'inductance s'exprime en henry dont le symbole est $H$
Remarque :
On admet quelque soit la forme du circuit, son flux propre a pour expression
$$\Phi=Li$$
$\Phi$ en $Wb$
$i$ en $A$
$L$ en $H$
4. $F.é.m$ d'auto-induction
4.1. Expression de la $f.é.m$ d'auto-induction
Lorsque le flux varie, il apparait une force électromotrice d'auto-induction
$e=-\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}\quad\text{or}\quad\Phi=Li$
$\Rightarrow e=-\dfrac{\mathrm{d}(Li)}{\mathrm{d}t}$
$\Rightarrow e=-L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
4.2. Tension aux bornes d'une bobine

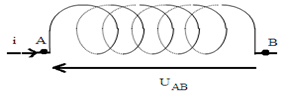
Soit $A$ et $B$ les bornes d'une bobine orientée arbitrairement de $A$ vers $B.$ Soit $i$ l'intensité instantanée du courant qui la parcourt et $r$ sa résistance. Lorsque la bobine est le siège d'une force électromotrice auto-induite. La loi d'Ohm généralisée s'écrit avec les conventions habituelles.
$e=-L\dfrac{\mathrm{d}i}{\mathrm{d}t}U_{AB}=ri-e\quad\text{or}\quad e=-L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
$\Rightarrow U_{AB}=ri+L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
5. Énergie stockée dans une bobine
5.1. Mise en évidence expérimentale
Rappel :
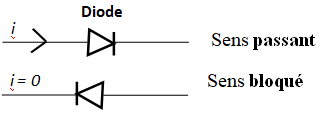
Une diode est un dipôle qui laisse passer le courant lorsqu'il est branché en « sens passant » et qui ne laisse pas passer le courant lorsqu'il est branché en « sens bloqué »


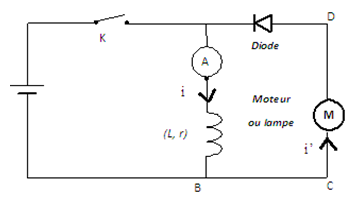
$\bullet\ $On ferme l'interrupteur $K.$ L'ampèremètre détecte un courant nul Le moteur ne tourne pas (la lampe ne s'allume pas) car la diode est dans le sens bloqué
$\bullet\ $On ouvre l'interrupteur $K$ : le moteur tourne (la lampe s'allume) un instant.
La bobine avait donc emmagasiné de l'énergie qu'elle a restituée au moteur (lampe) sous la forme d'un courant de sens passant
5.2. Expressions de la puissance et de l'énergie électriques échangées
$\bullet\ $Expression de la puissance électrique échangée
La puissance instantanée échangée par le dipôle (bobine) avec le reste du circuit a pour expression
$P=U_{AB}^{i}\quad\text{or}\quad U_{AB}=ri+L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
$\Rightarrow P=\left(ri+L\dfrac{\mathrm{d}i}{\mathrm{d}t}\right)i=ri^{2}+Li\dfrac{\mathrm{d}i}{\mathrm{d}t}$
$\Rightarrow P=ri^{2}+\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{1}{2}Li^{2}\right)$
La puissance instantanée échangée par un solénoïde apparait comme la somme de deux termes :
$-\ $la puissance dissipée par effet Joule : $P_{j}=ri^{2}$
$-\ $la puissance (magnétique) emmagasinée par la bobine : $P_{m}=\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{1}{2}Li^{2}\right)$
$\bullet\ $Expression de l'énergie électrique échangée
L'énergie emmagasinée par la bobine est donnée par la relation :
$$E_{L}=\int P_{m}\mathrm{d}t=\int_{0}^{1}\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{1}{2}Li^{2}\right)\mathrm{d}t=\int_{0}^{1}\mathrm{d}\left(\dfrac{1}{2}Li^{2}\right)$$
$$\Rightarrow E_{L}=\dfrac{1}{2}Li^{2}$$
$E_{L}$ en joules $(J)$
$L$ en henrys $(H)$
$i$ en ampères $(A)$
III. Étude d'une bobine $(R\;,\ L)$
1. Étude expérimentale de l'établissement du courant dans une bobine
Soit le montage suivant :
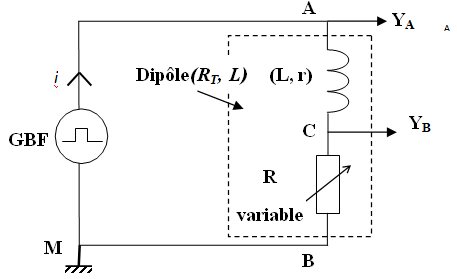
$-\ $La voie $Y_{A}$ de l'oscilloscope visualise la tension $U_{AM}$ qui correspond à la tension aux bornes du dipôle $(R\;,\ L)$, mais aussi à la tension délivrée par le générateur $G.B.F$ (générateur de basse fréquence)
$-\ $La voie $Y_{B}$ visualise la tension $U_{BM}$ aux bornes du conducteur ohmique qui correspond à l'allure de l'intensité du courant à un facteur près
$\bullet\ $Observations
On obtient un oscillogramme. On constate que :
$-\ $lors de la mise sous tension du circuit, le courant n'atteint pas immédiatement son maximum
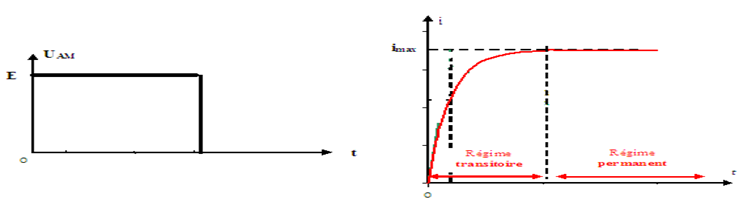
L'établissement du courant dans un circuit comportant une bobine n'est pas instantané. Il se décompose deux parties :
$-\ $un régime transitoire pendant lequel l'intensité du courant augmente
$-\ $un régime permanent pendant lequel l'intensité du courant atteint sa valeur maximale
2. Étude théorique
2.1. Établissement du courant
$\bullet\ $Équation différentielle
La constante de temps $\tau$ nous renseigne sur la rapidité avec laquelle s'effectue la rupture du courant dans le circuit
$\bullet\ $Détermination de la constante de temps $\tau$
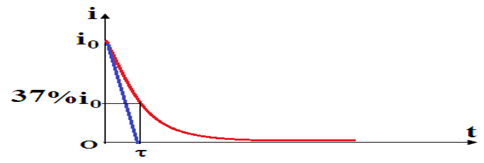
On peut déterminer graphiquement l'abscisse $\tau$ de deux façons différentes :
$-\ $en traçant la tangente à la courbe $i(t)$ au point d'abscisse $t=0.$ Cette courbe $i=0$ au point d'abscisse $t=\tau$
$-\ $en se plaçant à l'ordonnée correspondant à $37\%$ $i_{0}$
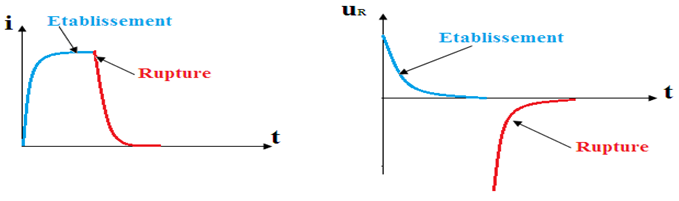
$-\ $L'intensité du courant ne subit pas de discontinuité lors du passage de l'établissement à la rupture du courant, tandis que la tension est discontinue

Ajouter un commentaire