ENSA - Épreuve de Sciences Physiques - 2015

 

Données :

 

$M(P)=151\;g/mol\;;\  M(\text{Anhydride})=102\;g/mol\;;\ M(P_{a})=109\;g/mol.$

 

Masse volumique de l'anhydride éthanoïque : $M=108\;g/c$

 

Le paracétamol $P$ est un antalgique dont le principe actif a pour formule semi-développée

 

 

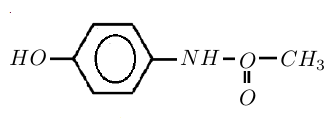
1) Retrouver les formules semi-développées de l'acide carboxylique et de l'amine dont il est issu.

 

2) Écrire alors l'équation bilan de la réaction correspondante.

 

3) On utilise plutôt l'anhydride acétique à la place de l'acide acétique pour faire la synthèse du paracétamol. 

 

Justifier. 

 

Écrire l'équation bilan de la réaction correspondante.

 

4) Le rendement de cette synthèse est égale à $79\%.$

 

Déterminer alors la masse d'anhydride acétique nécessaire à la synthèse de $m(P)=3\;g$ de paracétamol contenue dans une boite de doliprane pour enfant.

 

5) Dans un erlenmeyer, on introduit maintenant $5.45\;g$ de paraminophénol et $7\;mL$ d'anhydride éthanoïque par petites portions successives. La masse de paracétamol obtenue est $6.04\;g$

 

a) Écrire la formule semi-développée du paraminophénol $(P_{a}).$

 

Quel est le réactif limitant.

 

b) Montrer que la réaction est incomplète.

 

c) Si la réaction était complète, quelle masse de paracétamol obtiendrait-on ?

1) L'huile de lin a pour composition massique : $5\%$ de palmitine $($acide palmitique $C_{15}H_{31}COOH).$

 

$5\%$ de stéarine $($acide stéarique $C_{17}H_{35}COOH)\;,\ 26\%$ d'oléine $($acide oléique $C_{17}H_{33}COOH)\;,\ 18\%$ de linoléine $($acide linoléique $C_{17}H_{31}COOH)\ $ et $\ 46\%$ de linolénine $($acide linolénique : $C_{17}H_{29}COOH).$

 

a) Écrire les formules brutes des cinq acides gras associés aux triglycérides ci-dessus (en mettant en évidence les doubles liaisons, préciser leurs nombres pour chaque acide insaturé).

 

b) Parmi les cinq triglycérides, quels sont ceux qui comportent des insaturations ?

 

2) On désire hydrogéner $1\;kg$ de cette huile. (Seuls les triglycérides insaturés sont concernés)

 

a) Écrire les équations-bilan des réactions d'hydrogénation

 

b) Quelle masse de corps gras hydrogéné obtient-on ?

 

c) Quel volume de dihydrogène, mesuré dans les conditions normales de température et de pression est nécessaire pour réaliser cette hydrogénation ?

 

d) Écrire les équations-bilan des réactions de saponification par la soude (hydroxyde de sodium) des composants de cette huile. 

 

Nommer les corps obtenus

 

3) Si on utilise $100\;g$ de cette huile, quelle masse totale de savon récupère-t-on ?

 

a) Quelle masse de glycérol s'est formée ?

 

b) Quelle masse de soude est nécessaire pour effectuer cette saponification ? 

 

Celle-ci se présente sous forme d'une lessive de soude de concentration molaire volumique $10\;mol/L.$

 

c) Quel volume de lessive de soude est nécessaire ?

Un ressort à spires non jointives, de masse négligeable et raideur $k=10\;N.m^{-1}$, a une longueur à vide : $l_{0}=20\;cm.$

 

Ce ressort est enfilé sur une tige horizontale (voir figure). 

 

L'une de ses extrémités est fixe, l'autre est attachée à un solide $S_{1}$ de masse $m_{1}=75\;g.$ 

 

Un dispositif convenable, non représenté, assure un guidage de l'ensemble. 

 

Le solide $S_{1}$ n'effectue ainsi que des mouvements de translation le long de l'axe $(O\;,\ \vec{i})$ axe du ressort.

 

Au repos le centre d'inertie $G$ de $S_{1}$ est en $O.$

 

Un solide $S_{2}$, de masse $m_{2}=25\;g$, heurte le solide $S_{1}$ avec une vitesse $\vec{v}_{2}$ dirigée vers la droite suivant l'axe du ressort.

 

Après choc, $S_{2}$ reste accroché à $S_{1}.$

 

 

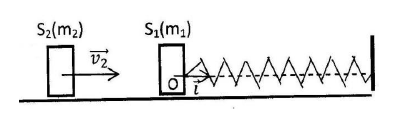
1) Déterminer la vitesse $\vec{v}$, immédiatement après le choc, de l'ensemble $S$ des deux solides $S_{1}\ $ et $\ S_{2}$ accrochés, sachant que $v_{2}=1\;m.s^{-1}.$

 

Indication : On admet que pendant le choc, le ressort n'exerce aucune force sur le solide $S_{1}.$

 

2) Établir l'équation différentielle qui régit le mouvement de $S.$

 

On prend comme origine des abscisses le point $O.$

 

3) Calculer : 

 

a) La pulsation propre de l'oscillateur, 

 

b) Sa période propre, 

 

c) Sa fréquence propre

 

4) Si l'origine des temps est l'instant du choc. 

 

Établir l'équation horaire du mouvement de $S.$

 

5) Donner l'expression de l'énergie mécanique du système puis la calculer.

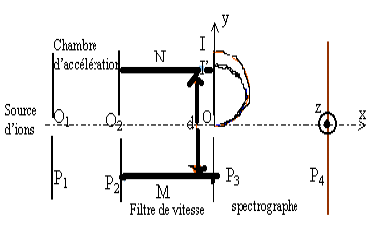
Des ions positifs isotopes d'un élément $(X)\;\ ^{68}X^{2+}\ $ et $\ ^{A}X^{2+}$ émis à partir du point $O_{1}$ avec une vitesse initiale négligeable, sont accélérés entre $O_{1}\ $ et $\ O_{2}$ par la tension $|U_{0}|=|U_{P_{1}P_{2}}|=5\;KV$ existant entre les plaques $P_{1}\ $ et $\ P_{2}.$

 

Ils se déplacent dans le vide suivant la direction $Ox.$ On négligera le poids devant les autres forces.

 

On donne : 

 

Charge élémentaire : $e=1.6\cdot 10^{-19}\;C$

 

Masse respective des isotopes $^{68}X^{2+}\ $ et $\ ^{A}X^{2+}\ :$

 

$m=68\;u\ $ et $\ m'=Au$ avec $u=1.67\cdot 10^{-27}kg$

 

 

1) Quel est le signe de la tension $U_{0}\ ?$

 

2) Calculer la vitesse $v$ de l'isotope $^{68}X^{2+}$ en $O_{2}.$

 

3) Si $v\ $ et $\ v'$ désignent respectivement les vitesses en $O_{2}$ des deux isotopes, donner la relation entre $v\;,\ v'\;,\ m\ $ et $\ m'.$

 

4) Le rapport $\dfrac{v^{'}}{v}=1.02$ en déduire la valeur entière $A$ du nombre de masse de l'ion $^{A}X^{2+}$

 

5) Arrivés en $O_{2}$, les ions pénètrent dans un filtre de vitesse constitué par deux plaques horizontales $M\ $ et $\ N$ distantes de $d=20\;cm$ entre lesquelles on établit une différence de potentiel $U=V_{M}-V_{N}=1.68\;kV$

 

Un dispositif crée dans l'espace inter-plaques un champ magnétique de direction $O_{2}z$, perpendiculaire aux vitesses $\vec{v}\ $ et $\ \vec{v}'$  ainsi qu'au champ électrique $\vec{E}$

 

a. Quel doit être le sens du champ magnétique $\vec{B}$ pour que les ions $^{68}X^{2+}$ arrivant en $O_{2}$ avec la vitesse $\vec{v}$ traversent le dispositif en ligne droite?

 

b) Exprimer $B$ en fonction de $v\;,\ U\;,\ d.$

 

Calculer $B$ en $mT.$

 

c) Répondre par vrai ou faux à la proposition suivante: « les ions $^{A}X^{2+}$ qui arrivent en $O_{2}$ avec la vitesse $\vec{v}$ sont déviés vers la plaque $N$ ». 

 

Justifier

 

d) Quelle doit être la valeur $\vec{B}'$ du champ magnétique pour que les ions $^{A}X^{2+}$ traversent le dispositif sans subir de déviation.

 

6) En faisant varier la valeur du champ magnétique dans le filtre de vitesse, on peut faire passer par le point $O$ l'un ou l'autre des isotopes. 

 

Les ions pénètrent alors dans un champ magnétique $\vec{B}_{0}$ dirigé suivant $Oz$ tel que $B0=0.5\;T$

 

a) Quel doit être le sens de ce champ pour que les ions soient déviés vers les y positifs?

 

b) Donner l'expression du rayon $R$ de la trajectoire de l'ion de masse $m$, de charge $q$ et de vitesse $v$

 

c) Exprimer la différence $R-R'$ des rayons des trajectoires que décrivent les deux sortes d'ions en fonction de $R\ $ et de $A.$

 

d) La distance entre les points d'impact $I\ $ et $\ I'$ sur la plaque $P_{3}$ est $II'=a=7.2\;mm$

 

Exprimer en fonction de $a\ $ et $\ R$ le nombre de masse $A$ de l'ion $^{A}X^{2+}$ et calculer sa valeur.

 

$$\text{Durée 2 heures}$$