Pour réaliser les $13.2\Omega$ devant protéger la lampe témoin de l'alarme de sa maison, un électricien ne dispose que de deux conducteurs de résistances respectives $R_{1}=22\Omega$ et $R_{2}=33\Omega$. Quel montage devra-t-il réaliser pour répondre à cette exigence du constructeur ?

 

 

Dans un circuit - série, le courant est partout le même : l'intensité du courant est constante

$I=I_{1}=I_{2}$

 

 

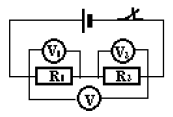
La tension aux bornes d'un groupement en série est égale à la somme des tensions

$U=U_{1}+U_{2}$

On vérifie à l'ohmmètre que la résistance $R_{e}$ du groupement que l'on appelle résistance équivalente est égale à la somme des résistances respectives des conducteurs en série.

$R_{e}=R_{1}+R_{2}$

 

N.B. Vérification théorique.

Appliquons la loi d'ohm au circuit. $U=R_{e}.I$

Or nous savons que $U_{1}=R_{1}.I_{1}$ ; $\ U_{2}=R_{2}.I_{2}$

Et que $U = U_{1} + U_{2}$

Que l'on peut écrire $R_{e}. I = R_{1} . I_{1} + R_{2} . I_{2} = (R_{1} + R_{2}) I$

On trouve donc $R_{e} = R_{1} + R_{2}$

 

 

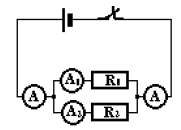
Dans un groupement en parallèle, l'intensité du courant principal est égale à la somme des intensités des courants circulant dans chacune des dérivations.

$I = I_{1} + I_{2}$

 

 

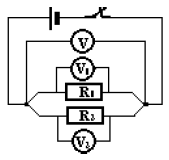
Dans un groupement en parallèle, la tension est la même aux bornes des différentes dérivations

$U = U_{1} = U_{2}$

La mesure à l'ohmmètre montre que la résistance équivalente est inférieure à la plus petite des résistances respectives des conducteurs associés en parallèle.

 

N.B. Expression théorique

En appliquant la loi d'ohm, on trouve

$I =\dfrac{U}{R_{e}}$;  $\ I_{1} =\dfrac{U}{R_{1}}$; $\ I_{2} =\dfrac{U}{R_{2}}$

Nous savons que $I = I_{1} + I_{2}$

Qu'on peut alors écrire : $\dfrac{U}{R_{e}}=\dfrac{U}{R_{1}}+\dfrac{U}{R_{2}}=U\left(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}\right)$ 

Ce qui donne : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$
 

Remarque : La résistance équivalente est celle du conducteur équivalent. Le conducteur équivalent est le conducteur qui, mis à la place du groupement, ne modifie ni la tension ni le courant dans le circuit.

Source: irempt.education.sn