Corrigé Bac Maths S2 2e groupe 2016
Exercice 1
1) a) Calculer $a^{2016}$
On vérifie aisément, en utilisant le module et l'argument du nombre complexe $a$ que l'écriture
exponentielle de ce nombre est $a=\sqrt{2}\mathrm{e}^{\mathrm{i}\tfrac{5\pi}{4}}$, d'où d'après la formule de MOIVRE :
\begin{eqnarray} a^{2016} &=& \left(\sqrt{2}\mathrm{e}^{\mathrm{i}\tfrac{5\pi}{4}}\right)^{2016} \nonumber \\ &=& 2^{1008}\mathrm{e}^{\mathrm{i}\tfrac{5\pi}{4}\times 2016} \nonumber \\ &=& 2^{1008}\mathrm{e}^{\mathrm{i}(504\times 5\pi)} \nonumber \end{eqnarray}
Soit $a^{2016}=2^{1008}\ ($car $504\times 5\pi=2520\pi$ étant multiple de $2\pi$, on a $\mathrm{e}^{\mathrm{i}(504\times 5\pi)}=1).$
b) Racines quatrièmes du nombre complexe $b$
On vérifie facilement que : $b=2\mathrm{e}^{\mathrm{i}\tfrac{\pi}{3}}$ Les racines quatrièmes de $b$ sont donc les nombres complexes de module $\sqrt[4]{2}$ et d'argument $\dfrac{\left(\tfrac{\pi}{3}\right)}{4}+\dfrac{2k\pi}{4}=\dfrac{\pi}{12}+\dfrac{k\pi}{2}\ (k\in\;\{0\;,\ 1\;,\ 2\;,\ 3\}).$
En d'autres termes, ce sont les nombres $$z_{k}=\sqrt[4]{2}\mathrm{e}^{\mathrm{i}\left(\tfrac{\pi}{12}+\tfrac{k\pi}{2}\right)}$$
$$z_{0}=\sqrt[4]{2}\mathrm{e}^{\mathrm{i}\tfrac{\pi}{12}}\;;\quad z_{1}=\sqrt[4]{2}\mathrm{e}^{\mathrm{i}\tfrac{7\pi}{12}}\;;\quad z_{2}=\sqrt[4]{2}\mathrm{e}^{\mathrm{i}\tfrac{13\pi}{12}}\;;\quad z_{3}=\sqrt[4]{2}\mathrm{e}^{\mathrm{i}\tfrac{19\pi}{12}}$$
2) a) Probabilité pour que $z$ soit un imaginaire pur
L'univers $\Omega$ est l'ensemble des couples de nombres pris dans
$$\{0\;,\ 1\;,\ 2\;,\ -1\}\times\{1\;,\ \sqrt{3}\;,\ 2\;,\ -1\}$$
$$Card\;\Omega=4\times 4=16$$
Pour que l'événement "$z$ est un imaginaire pur" soit réalisé, il faut que le jeton vert porte le numéro 0, le second, rouge, pouvant porter n'importe lequel des numéros 1, $\sqrt{3}$, 2, -1. La probabilité de cet événement, que nous noterons $A$, est donc, d'après l'hypothèse d'équiprobabilité : $$p(A)=\dfrac{1\times 4}{4\times 4}$$
b) Probabilité pour que l'image de $z$ soit sur le cercle de centre $O$ et de rayon $\sqrt{2}.$
Le nombre complexe obtenu $z$ a pour module $\sqrt{2}$ si et seulement si on a "tiré" les couples $(1\;,\ 1)$ ou $(1\;,\ -1)$ ou $(-1\;,\ 1)$ ou $(-1\;,\ -1).$
Il y a donc 4 couples (sur 16) qui réalisent cet événement, que nous noterons $B.$
Par conséquent, $$p(B)=\dfrac{4}{16}=\dfrac{1}{4}$$
c) Probabilité pour qu'un argument de $z$ soit $\dfrac{\pi}{4}$ ou $\dfrac{3\pi}{4}$
Si cet événement $C$ est réalisé, c'est qu'on a eu un des couples $(1\;,\ 1)$ ou $(2\;,\ 2)$ ou $(-1\;,\ 1)$ ou $(-1\;,\ -1).$
En effet, dire qu'un argument de $z$ est $\dfrac{\pi}{4}$ ou $\dfrac{3\pi}{4}$ revient à dire que l'on a $x=y$ (avec $x>0)$ ou que $x=-y$ (avec $x<0).$
Il y a donc 4 couples (sur 16) qui réalisent $C$, d'où
$$p(C)=\dfrac{1}{4}$$
Exercice 2
1) Résolution de l'équation différentielle $(E_{1})\ :\ y''+2y'+2y=0$
Son équation caractéristique est : $r^{2}+2r+2=0.$
Elle a pour discriminant (réduit) $\Delta'=\mathrm{i}^{2}$ et on vérifie aisément que ses racines sont $z_{1}=-1+\mathrm{i}$ et $z_{2}=-1-\mathrm{i}.$
Les solutions de cette équation différentielle sont donc les fonctions $y$ de la forme :
$$\mathrm{e}^{-x}(A\cos x+B\sin x)$$
2) Recherche d'une fonction polynôme $P$ du premier degré solution de $(E_{2}).$
Posons $y=ax+b$. On a alors $y'=a$ et $y''=0$, d'où en remplaçant dans l'équation différentielle $(E_{2})$
\begin{eqnarray} y''+2y'+2y=x+1 &\Rightarrow& 0+2a+2(ax+b)=x+1 \nonumber \\ &\Rightarrow& 2ax+2a+2b=x+1 \nonumber \end{eqnarray}
Par identification de ces deux polynômes, il vient alors : $$\left\lbrace\begin{array}{rcl} 2a &=& 1 \\ \\ a+b &=& \dfrac{1}{2} \end{array}\right.\;,\quad\text{soit }:\ \left\lbrace\begin{array}{rcl} a &=& \dfrac{1}{2} \\ \\ b &=& 0 \end{array}\right.$$
On en conclut que le polynôme $P=\dfrac{1}{2}x$ est solution de l'équation différentielle $(E_{2}).$
3) Condition nécessaire et suffisante pour qu'une fonction $f$ soit solution de $(E_{2})$
\begin{eqnarray} f\;\text{ est solution de }\;(E_{2}) &\Leftrightarrow& f''+2f'+2f=x+1 \nonumber \\ &\Leftrightarrow& f''+2f'+2f=P''+2P'+2P\ (\text{car }P\text{ est solution de }\;(E_{2})) \nonumber \\ &\Leftrightarrow& f''-P''+2(f'-P')+2(f-P)=0 \nonumber \\ & & (\text{ en transposant dans le premier membre }) \nonumber \\ &\Leftrightarrow& (f-P)''+2(f'-P')+2(f-P)=0 \nonumber \\ &\Leftrightarrow& (f-P)\;\text{ est solution de }\;(E_{1}) \nonumber \end{eqnarray}
4) Forme générale des solutions de $(E_{2}).$
D'après la question précédente, les solutions de $(E_{2})$ sont donc les fonctions $f$ de la forme $f=P+y$, où $y$ est une solution de $(E_{1}).$
L'ensemble des solutions de $(E_{2})$ est donc, d'après 1), l'ensemble des fonctions $f$ de la forme $$f=\dfrac{1}{2}x+\mathrm{e}^{-x}(A\cos x+B\sin x)$$
5) Détermination d'une solution particulière de $(E_{2})$
Les conditions posées sur $h$ se traduisent par : $\left\lbrace\begin{array}{rcl} h(0) &=& 1 \\ \\ h'(0) &=& \dfrac{1}{2} \end{array}\right.$
$h$ étant une solution particulière de $(E_{2})$,
on a $h=\dfrac{1}{2}x+\mathrm{e}^{-x}(A\cos x+B\sin x)$,
d'où (utiliser les formules de dérivation) : $$h'=\dfrac{1}{2}+\mathrm{e}^{-x}[(B-A)\cos x+(-A-B)\sin x)]$$
Les conditions deviennent alors $\left\lbrace\begin{array}{rcl} A &=& 1 \\ \\ \dfrac{1}{2}+B-A &=& \dfrac{1}{2}\end{array}\right.$
ce qui entraine que : $A=B=1$
On obtient la solution particulière $h=\dfrac{1}{2}x+\mathrm{e}^{-x}(\cos x+\sin x)$
6) Calcul $\int_{0}^{\pi}h(x)\mathrm{d}x$
On a tout d'abord : $\int_{0}^{\pi}h(x)\mathrm{d}x=\left[\dfrac{1}{2}\dfrac{x^{2}}{2}\right]_{0}^{\pi}+\int_{0}^{\pi}\mathrm{e}^{-x}(\cos x+\sin x)\mathrm{d}x\qquad(*)$
Posons $I_{1}=\int_{0}^{\pi}\mathrm{e}^{-x}\cos x\mathrm{d}x$ et $I_{2}=\int_{0}^{\pi}\mathrm{e}^{-x}\sin x\mathrm{d}x$
On intègre $I_{1}$ par parties en posant : $\left\lbrace\begin{array}{rcl} u(x) &=& \mathrm{e}^{-x} \\ v'(x) &=& \cos x \end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{rcl} u'(x) &=& -\mathrm{e}^{-x} \\ v(x) &=& \sin x \end{array}\right.$
La formule d'intégration par parties s'écrit alors : $I_{1}=[\mathrm{e}^{-x}\sin x]_{0}^{\pi}+I_{2}$
L'expression entre crochets étant visiblement nulle (car $\sin x$ s'annule aussi bien en $\pi$ qu'en 0), on a $I_{1}=I_{2}\qquad(**)$
Intégrons alors $I_{2}$ par parties en posant : $\left\lbrace\begin{array}{rcl} u(x) &=& \mathrm{e}^{-x} \\ v'(x) &=& \sin x \end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{rcl} u'(x) &=& -\mathrm{e}^{-x} \\ v(x) &=& -\cos x \end{array}\right.$
D'où : $I_{2}=[-\mathrm{e}^{-x}\cos x]_{0}^{\pi}-\underbrace{\int_{0}^{\pi}\mathrm{e}^{-x}\cos x\mathrm{d}x}_{I_{1}}$
On reconnait $I_{1}$ dans la dernière intégrale au second membre. On en déduit en tenant compte de $(**)$ qu'on a donc : $2I_{1}=[-\mathrm{e}^{-x}\cos x]_{0}^{\pi}=\mathrm{e}^{-\pi}+1$
Par suite, d'après $(*)\ :$
$$\int_{0}^{\pi}h(x)\mathrm{d}x=\dfrac{\pi^{2}}{4}+\mathrm{e}^{-\pi}+1$$
Exercice 3
1) a) Étude des variations de $f\ :\ x\mapsto\ (x-2)\mathrm{e}^{x}$
• $f$ est définie et dérivable sur $\mathbb{R}$ comme produit de fonctions dérivables et pour tout $x$ réel, on a : $f'(x)=\mathrm{e}^{x}+(x-2)\mathrm{e}^{x}=(x-1)\mathrm{e}^{x}$
• \begin{eqnarray} \lim_{x\rightarrow -\infty}f(x) &=& \lim_{x\rightarrow -\infty}[(x-2)\mathrm{e}^{x}] \nonumber \\ &=& \lim_{x\rightarrow -\infty}[x\mathrm{e}^{x}-2\mathrm{e}^{x}] \nonumber \\ &=& 0\quad \text{(par somme et en utilisant les limites usuelles)}\nonumber \end{eqnarray}
• $\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}[(x-2)\mathrm{e}^{x}]=+\infty$
car l'on a $\left\lbrace\begin{array}{rcl} \lim_{x\rightarrow +\infty}(x-2) &=& +\infty \\ \lim_{x\rightarrow +\infty}\mathrm{e}^{x} &=& +\infty \end{array}\right.$
d'où le résultat par produit.
On en déduit le tableau de variation suivant :
$$\begin{array}{|c|lcccccr|} \hline x&-\infty& &1& &0& &+\infty \\ \hline f'(x)& &-&|&+&\vdots&+& \\ \hline &0& &|& &\vdots& &+\infty \\ & &\searrow&|& &\vdots&\nearrow& \\ f& & &|& &0& & \\ & & &|&\nearrow& & & \\ & & &-\mathrm{e}& & & & \\ \hline\end{array}$$
b) Le point d'abscisse 0 de la courbe de $f$ est un point d'inflexion
D'après l'expression précédente de $f'(x)$, on peut dire que $f'$ est dérivable sur $\mathbb{R}$ et que pour tout réel $x$, sa dérivée qui n'est autre que la dérivée seconde de $f$ est donnée par : $$f''(x)=\mathrm{e}^{x}+(x-1)\mathrm{e}^{x}=x\mathrm{e}^{x}$$
Il est alors clair que $f''$ s'annule en changeant de signe en $x_{0}=0.$ On en déduit que le point d'abscisse 0 est bien un point d'inflexion de $(C_{f}).$
2) a) Courbe représentative de $f$
Notons d'abord que $\lim_{x\rightarrow +\infty}\left[\dfrac{f(x)}{x}\right]=\lim_{x\rightarrow +\infty}\left[\dfrac{x-2}{x}\mathrm{e}^{x}\right]=+\infty$ car l'on a $\left\lbrace\begin{array}{rcl} \lim_{x\rightarrow +\infty}\left(\dfrac{x-2}{x}\right) &=& 1 \\ \\ \lim_{x\rightarrow +\infty}\mathrm{e}^{x} &=& +\infty \end{array}\right.$ d'où le résultat par produit.
Au voisinage de $+\infty$, la courbe $(C_{f})$ admet donc une branche parabolique de direction $(O\;;\ \vec{j}).$
Avec le tableau de variation ci-dessus, on en déduit que la courbe a l'allure ci-dessous :
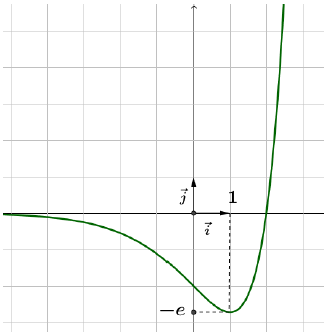
Au vu de la courbe, une droite horizontale (d'équation $x=k$) coupe la courbe en deux points si et seulement si $k\in[-\mathrm{e}\;;\ 0[$ (ce que le tableau de variation confirme par ailleurs car il indique que $f$ prend deux fois toutes les valeurs de $[-\mathrm{e}\;;\ 0[).$
Exercice 4
1) a) Calcul du terme manquant $a$ dans le tableau statistique
La série était définie par : $$\begin{array}{|c|c|c|c|c|c|}\hline X&5&8&9&a&10 \\ \hline Y&6&7&b&9&11 \\ \hline\end{array}$$
D'après la formule $\bar{X}=\dfrac{\sum_{i=1}^{n}x_{i}}{N}$,
le fait que $\bar{X}=7.8$ se traduit par : $\dfrac{5+8+9+a+10}{5}=7.8$,
soit $32+a=5\times 7.8=39$, ce qui équivaut à : $a=7.$
b) Calcul du terme manquant $b$ dans le tableau statistique
D'après la formule $V(Y)=\dfrac{\sum_{i=1}^{n}y_{i}^{2}}{N}-\bar{Y}^{2}$,
le fait que $var(Y)=2.96$ se traduit par :
$\dfrac{6^{2}+7^{2}+b^{2}+9^{2}+11^{2}}{5}-\left(\dfrac{6+7+9+11+b}{5}\right)^{2}=2.96$,
soit : $\dfrac{b^{2}+287}{5}-\dfrac{(b+33)^{2}}{25}=2.96$
Après réduction au même dénominateur et simplification, on aboutit à : $4b^{2}-66b+272=0$, équation du second degré en $b$ dont les solutions sont $b_{1}=8.5$ et $b_{2}=8.$
Comme l'énoncé impose que $b<8.5$ on a nécessairement $b=8$
c) Calcul du coefficient de corrélation et interprétation
D'après les résultats précédents, on a maintenant le tableau suivant pour la série statistique étudiée : $$\begin{array}{|c|c|c|c|c|c|}\hline X&5&8&9&7&10 \\ \hline Y&6&7&8&9&11 \\ \hline\end{array}$$
Calculons alors certaines caractéristiques de cette série.
Nous savons déjà que $\bar{X}=7.8$ et que $V(Y)=2.96$
Il nous faut calculer la variance $V(X)$ de $X$ et la covariance $\sigma_{XY}.$
On a successivement :
$V(X)=\dfrac{\sum_{i=1}^{n}x_{i}^{2}}{N}-\bar{X}^{2}=2.9$ puis $\bar{Y}=\dfrac{\sum_{i=1}^{n}y_{i}}{N}=8.2$
et enfin $\sigma_{XY}=\dfrac{\sum_{i=1}^{n}x_{i}y_{i}}{N}-\bar{X}\times\bar{Y}=2.24$
d'où l'on déduit que le coefficient de corrélation $r=\dfrac{\sigma_{XY}}{V(X)\times V(Y)}$ vaut environ 0.757
Cette valeur étant inférieure à 0.87 on estime qu'il y a une faible corrélation entre $X$ et $Y.$
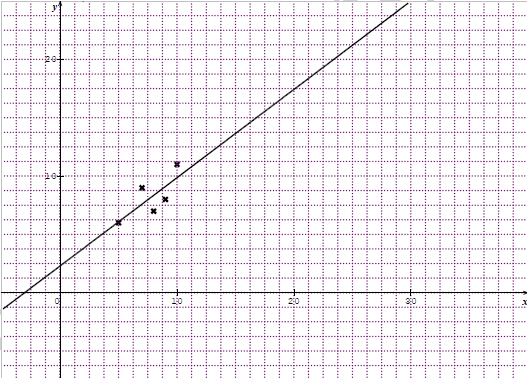
Voici le nuage de points ainsi que la droite de régression :

Ajouter un commentaire