BFEM Mathématiques 2025
Exercice 1 : 6 points
Pour chacune des questions dans le tableau ci-dessous, trois réponses A, B et C sont proposées dont une seule est correcte. Pour répondre, tu porteras sur ta copie, le numéro de la question suivi de la lettre correspondant à ta réponse choisie.
Chaque réponse correcte est notée 0,75 point. Une réponse fausse ou une absence de réponse est notée 0 point.
| N° | Questions | A | B | C |
|---|---|---|---|---|
| 1 | Soit SUR un triangle rectangle en R tel que $\sin(\widehat{RSU}) = \frac{\sqrt{3}}{2}$ et SR = 3 cm. Quelle est la longueur du segment [SU] ? | $6\sqrt{3}$ cm | $\frac{3\sqrt{3}}{2}$ cm | $2\sqrt{3}$ cm |
| 2 | Quel est l'ensemble des solutions dans $\mathbb{R}$ de l'inéquation $(3 - 2x)(1 - x) < 0$ ? | $[1; \frac{3}{2}]$ | $\{1 ; \frac{3}{2}\}$ | $]1 ; \frac{3}{2} [$ |
| 3 | Dans le plan muni d'un repère orthonormé $(O; \vec{i}, \vec{j})$, quel est le couple de coordonnées de A' image du point A(3, -2) par la translation de vecteur $\vec{u}(-1, 2)$ ? | $(2, 0)$ | $(–3, –4)$ | $(1, 0)$ |
| 4 | Quelle est l’expression littérale de l’application affine f telle que $g(3) = 3$ et $g(1) = –1$ ? | $–2x + 3$ | $2x – 3$ | $–2x -3$ |
| 5 | Quel est le couple solution du système d’équations $5x - 2y = 7$ et $-3x + 4y + 7 = 0$ ? | $(3, 4)$ | $(1, -1)$ | $(–3, –4)$ |
| 6 |
Sur la figure ci-contre, on a : $HK = 4$ , $AF = 5$, $LK = 6 $et $KF = x$. 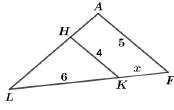 Pour quelle valeur de $x$ les droites $(HK)$ et $(AF)$ sont-elles parallèles ? |
$x = 24$ | $x=\frac{15}{2}$ | $x=\frac{3}{2}$ |
| 7 | Quelle est l’écriture simplifiée du réel $M = |3\sqrt{2} - 5| + 3\sqrt{(1 - 2)^2} - 6 - \sqrt{12}$ ? | $-6\sqrt{2} - \sqrt{12}$ | $-6 - 2\sqrt{3}$ | $-10 - \sqrt{12}$ |
| 8 | Dans un cercle, $x$ est la mesure en degré d'un angle inscrit, $y$ est la mesure en degré de l'angle au centre interceptant le même arc que l'angle inscrit. Quelle est la relation entre $x$ et $y$ ?? | $\frac{x}{y} =2$ | $\frac{y}{x} =2$ | $\frac{y}{x} =1$ |
Exercice 2 : 6 points.
Le service comptabilité d'une entreprise dispose des chiffres d'affaires de ses 50 points de vente pour le mois de décembre 2024.
| 9016 | 9551 | 10179 | 9070 | 10510 | 8859 | 9460 | 10024 | 9936 | 9994 |
| 9393 | 9502 | 9219 | 9825 | 9845 | 9417 | 9345 | 10188 | 10652 | 10266 |
| 9852 | 9627 | 9771 | 9897 | 10140 | 10310 | 9186 | 9851 | 9947 | 8724 |
| 9729 | 9877 | 9370 | 9896 | 9688 | 9188 | 9107 | 9130 | 8553 | 10237 |
| 9118 | 9675 | 9286 | 9388 | 8247 | 8829 | 9595 | 10303 | 9500 | 9878 |
1. On regroupe ces données brutes par classes d'amplitude 500.
La première classe ayant cette série statistique est [8000, 8500[.
Dresse un tableau statistique comportant les classes d'effectifs, les fréquences et les fréquences cumulées décroissantes.
$\textbf{4 × 0,5 pt = 2 pts}$
2. Calcule le chiffre d'affaires moyen.
$\textbf{1 pt}$
3. Quel est le pourcentage de points de vente ayant réalisé un chiffre d'affaires CA tel que 9000 ≤ CA < 10500 ?
$\textbf{1 pt}$
4. En utilisant la méthode de Thalès, calcule $m_e$ la médiane de cette série.
$\textbf{2 pts}$
$ \textbf{Problème : 8 points}$
L'unité de longueur est le décimètre.
Partie I
On considère un cône de révolution de hauteur 12 et de rayon de base 3,5.
$(\textit{On donnera les résultats en prenant $\pi \approx 3,14$}.)$
1. Montre que la génératrice du cône mesure 12,5.
$\textbf{0,5 pt}$
2. Calcule l'aire latérale $A_L$ du cône.
$\textbf{1 pt}$
3. Calcule le volume $V$ du cône.
$\textbf{1 pt}$
4. On effectue une section de ce cône par un plan parallèle à sa base pour obtenir un tronc de cône.
Sachant que la distance de la section à la base du cône est égale à $\frac{3}{5}$, détermine la hauteur de ce tronc de cône.
$\textbf{1,5 pt}$
Partie II
Un entrepreneur reçoit une commande de 100 bornes identiques de la part d'une commune. Ces bornes sont destinées à la délimitation de parcelles nouvellement aménagées.
Une borne a pour forme celle du tronc de cône précédent.
1. Sachant que les bornes sont fabriquées en béton armé de masse volumique 3000 kg/m³, c'est-à-dire chaque mètre cube de béton a une masse de 3000 kilogrammes, calcule en kilogrammes la masse de béton armé nécessaire pour fabriquer les 100 bornes. (On donnera le résultat à l'unité près pour une borne).
$\textbf{2 pts}$
2. La commune souhaiterait aussi recouvrir la surface latérale de chacune des 100 bornes par une couche de peinture.
Sachant que le pot de peinture couvre une surface d'aire 1 m² et coûte 5000 F, calcule la dépense en peinture.
$\textbf{2 pts}$

Commentaires
Anonyme (non vérifié)
dim, 11/23/2025 - 20:30
Permalien
<!DOCTYPE html>
Ajouter un commentaire