Corrigé mathématique du 1er groupe - S2 S2A S4 S5 - 2024-2025

Exercice 1

A. Soit deux nombres complexes $z_{1}$, $z_{2}$ non nuls.

Rappelons les propriétés algébriques suivantes :

1. $\left|\dfrac{z_{1}}{z_{2}}\right|=\dfrac{\left|z_{1}\right|}{\left|z_{2}\right|}$

2. $\arg\left(\dfrac{z_{1}}{z_{2}}\right)=\arg\left(z_{1}\right)-\arg\left(z_{2}\right)\left[2\pi\right]$

3. $\left|z_{1}\times z_{2}\right|=\left|z_{1}\right|\times\left|z_{2}\right|$

4. $\arg\left(z_{1}\times z_{2}\right)=\arg\left(z_{1}\right)+\arg\left(z_{2}\right)[2\pi]$

B. On considère le polynôme $P$ défini par :

$P(z)=z^{3}+\left(4-5\vec{i}\right)z^{2}-\left(5+12\vec{i}\right)z-8+\vec{i}$ où $z\in\mathbb{C}$

1. Montrons que $P$ admet une racine imaginaire pure $\beta$ que l'on déterminera.

Posons $\beta=\vec{i}x$ où $x\in\mathbb{R}$

$\begin{array}{rcl} P(\beta)=0&\Leftrightarrow&\left(\vec{i}x\right)^{3}+\left(4-5\vec{i}\right)\left(\vec{i}x\right)^{2}-\left(5+12\vec{i}\right)\left(\vec{i} x\right)-8+\vec{i}=0\\ &\Leftrightarrow& -\vec{i}x^{3}-\left(4-5\vec{i}\right)x^{2}-5\vec{i}x+12x-8+\vec{i}=0\\ &\Leftrightarrow&-\vec{i}x^{3}-4x^{2}+5\vec{i}x^{2}-5\vec{i}x+12x-8+\vec{i}=0\\ &\Leftrightarrow&-4x^{2}+12x-8+\vec{i}\left(-x^{3}+5x^{2}-5x+1\right)=0\\
&\Leftrightarrow&\left\lbrace\begin{array}{rcl} -4x^{2}+12x-8&=&0\quad (1)\\ -x^{3}+5x^{2}-5x+1&=&0\quad (2)
\end{array}\right. \end{array}$

$(1)\Leftrightarrow -x^{2}+3x-2=0$ Or $-1+3-2=0$ donc $x_{1}=1$ est une racine de $(1)$ ; d'où $x_{2}=\dfrac{c}{a}=2$

En remplaçant les solutions de $(1)$ dans $(2)$, on a

$-(1)^{3}+5(1)^{2}-5(1)+1=-1+5-5+1=0$

et

$-(2)^{3}+5(2)^{2}-5(2)+1=-8+20-10+1=3\ ;\ 3\neq 0$

Donc $x=1$ est solution du système, d'où $\beta=\vec{i}$

Commentaire : Pour l'équation $(1)$ du système, si le candidat

$-\ $calcule le discriminant $\Delta$ et trouve $\Delta=1$,

$-\ $ensuite, obtient les racines de l'équation a laide de, alors vous lui donnez 0125 point.

Pour l'équation $(2)$, si le candidat

$-\ $vérifie e que $1$ est racine de $(2)$ en faisant la somme des coefficients,

$-\ $ensuite, utilise la méthode de la division euclidienne ou la méthode d identification des
coefficients ou la méthode de Horner pour déterminer le polynôme $g$ tel que $-x^{3}+5x^{2}-5x+1=(x-1)g(x)$,

$-\ $puis, résout l'équation $g(x)=0$ pour trouver les autres solutions de $(2)$,

alors vous lui donnez $0.125$ point.

Enfin, sil trouve que $1$ est la solution commune de $(1)$ et $(2)$ et donne $\beta=\vec{i}$, alors vous lui donnez $0.25$ point

2.a.Déterminons le polynôme $g$ tel que $P(z)=\left(z-\vec{i}\right)g(z)$
$$\begin{array}{|c|c|c|c|c|} \hline &1&4-5\vec{i}&-5-12\vec{i}&-8+\vec{i}\\ \hline \vec{i}&&\vec{i}&4\vec{i}+4&-\vec{i}+8\\ \hline &1&4-4\vec{i}&-1-8\vec{i}&0\\ \hline \end{array}$$

$g(x)=z^{2}+(4-4\vec{i})z-1-8\vec{i}$

b. Factorisations $g(z)$

Calculons le discriminant réduit de $g$

$\begin{array}{rcl} \Delta'&=&(2-2\vec{i})^{2}+1+8\vec{i}\\&=&4-4-8\vec{i}+1+8\vec{i}\\&=&1 \end{array}$

$g$ admet deux racines :

$\begin{array}{rcl} z_{1}&=&\dfrac{-b'-\sqrt{\sqrt{\Delta'}}}{\alpha}\\&=&-2+2\vec{i}-1\\&=&-3+2\vec{i}
\end{array}$ et

$\begin{array}{rcl} z_{2}&=&\dfrac{-b'+\sqrt{\Delta'}}{\alpha}\\&=&-2+2\vec{i}\\&=&-1+2\vec{i} \end{array}$

Donc $g(z)=\alpha\left(z-z_{1}\right)\left(z-z_{2}\right)=\left(z+3-2\vec{i}\right)(z+1-2\vec{i})$

D'où $P(z)=(z-\vec{i})(z+3-2\vec{i})(z+1-2\vec{i})$

3.Dans le plan complexe muni d'un repère orthonormé direct $(O\ ;\ \vec{i}\;,\vec{j} )$ d'unité $1\,cm$, on considéré les points $A$ $B$ et $C$ d'affixes respectives $z_{A}=-1+2\vec{i}$, $z_{B}=-3+2\vec{i}$ et $z_{C}=\vec{i}$

On posez $z=\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}$

a. Flacons les points $A$, $B$ et $C$ dans le repère (Voir figure).

b. Déterminons le module et un argument de $z$

On a : $\begin{array}{rcl} z&=&\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\\&=&\dfrac{\vec{i}+1-2\vec{i}}{-3+2\vec{i}+1-2\vec{i}}\\&=&\dfrac{1-\vec{i}}{-2}\\&=&-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\\&=&\dfrac{1}{2}\left(-1+\vec{i}\right)\\&=&\dfrac{1}{2}\times \sqrt{2}\left(-\dfrac{1}{\sqrt{2}+\dfrac{1}{\sqrt{2}}\vec{i}}\right)\\&=&\dfrac{\sqrt{2}}{2}\left(\cos\dfrac{3\pi}{4}+\vec{i}\sin\dfrac{3\pi}{4}\right) \end{array}$

D'où, $|z|=\dfrac{\sqrt{2}}{2}$

$\arg(z)=\dfrac{3\pi}{4}[2\pi]$

$\left(\overbrace{\overrightarrow{AB}\;,\overrightarrow{AC}}\right)=\arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=\dfrac{3\pi}{4}$

Commentaire:si,a partir de la forme algébrique de $z$, le candidat

$-\ $calcule directement le module,

$-\ $ensuite,de termine un de ses arguments, alors vous lui donnez

4. Soit $S$ la similitude plane directe qui laisse invariant $A$ et transforme $B$ en $C$

a. Donnons l'écriture complexe de $S$

Soit $h\ :\ C\longrightarrow\,C$

où $a$, $b\in\mathbb{C}$, l'application associée à $S$

$x\mapsto\,az+b$

$S(A)=A\Longleftrightarrow\,h\left(z_{A}\right)=z_{A}\Longleftrightarrow\alpha z_{A}+b=z_{A}$

$\Longleftrightarrow\alpha(-1+2\vec{i})+b=-1+2\vec{i}\quad (1)$

$\begin{array}{rcl} S(B)&=&C\\&\Longleftrightarrow&h\left(z_{B}\right)\\&=&z_{C}\\&\Longleftrightarrow&\alpha z_{B}+b\\&=&z_{C} \end{array}$

$\Longleftrightarrow\alpha\left(-3+2\vec{i}\right)+b=\vec{i}\quad (2)$

$\left\lbrace\begin{array}{rcl} \alpha(-1+2\vec{i}+b&=&-1+2\vec{i}\quad (1)\\\alpha(-3+2\vec{i})+b&=&\vec{i}\quad (2) \end{array}\right.$

$\begin{array}{rcl} (1)-(2)&\Longleftrightarrow&\alpha\left(-1+2\vec{i}+3-2\vec{i}\right)\\&=&-1+2\vec{i}-\vec{i }\\&\Longleftrightarrow&2\alpha\\&=&-1+\vec{i}\\&\Longleftrightarrow&\alpha\\&=&-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}
\end{array}$

$\begin{array}{rcl} (2)&\Longleftrightarrow&\left(-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\right)\left(-3+2\vec{i}\right)+b\\&=&\vec{i}\\&\Longleftrightarrow&\dfrac{3}{2}-\vec{i}-\dfrac{3}{2}\vec{i}-1+b\\&=&\vec{i}\\&\Longleftrightarrow&\dfrac{1}{2}-\dfrac{5}{2}\vec{i} +b\\&=&\vec{i} \end{array}$

$\begin{array}{rcl} &\Longleftrightarrow& b\\&=&-\dfrac{1}{2}+\dfrac{5}{2}\vec{i}+\vec{i}\\&\Longleftrightarrow&b\\&=&-\dfrac{1}{2}+\dfrac{7}{2}\vec{i} \end{array}$

$\begin{array}{rcl} \alpha&=&-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\\&\text{ et }&b\\&=&-\dfrac{1}{2}+\dfrac{7}{2}\vec{i} \end{array}$

$h\ :\ C\longrightarrow C$

$z\mapsto\left(-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\right)z-\dfrac{1}{2}+\dfrac{7}{2}\vec{i}$

Commentaire : si le candidat propose $S\ :\ P\longrightarrow P$

$M(z)\mapsto M\left(z'\right)$

avec $z'=\left(-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\right)z-\dfrac{1}{2}+\dfrac{7}{2}\vec{i}$, alors vous lui donnez

Donnons l'écriture analytique de $S$

Posons $z=x+\vec{i}y$ et $z'+\vec{i}y'$ où $x\;,y\;,x'$ et $y'\in\mathbb{R}$

$\begin{array}{rcl} z'&=&h(x)\\&\Longleftrightarrow&x'+\vec{i}y'&=&\left(-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\right)\left(x+\vec{i}y\right)-\dfrac{1}{2}+\dfrac{7}{2}\vec{i}\\&\Longleftrightarrow&x'+\vec{i}y'&=&-\dfrac{1}{2}x-\dfrac{1}{2}y-\dfrac{1}{2}+\vec{i}\left(\dfrac{1}{2}x-\dfrac{1}{2}y+\dfrac{7}{2}\right)\&\Longleftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&-\dfrac{1}{2}x-\dfrac{1}{2}y-\dfrac{1}{2}
y'&=&\dfrac{1}{2}x-\dfrac{1}{2}y+\dfrac{7}{2} \end{array}\right. \end{array}$

b. Éléments caractéristiques de $S$

On sait que $S$ est la similitude plane directe de centre $A$ par hypothèse.

Déterminons son rapport $k$ et son angle $\theta$

$\begin{array}{rcl} k&=&|\alpha|\\&=&\left|-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\right|\\&=&\dfrac{\sqrt{2}}{2} \end{array}$

$\begin{array}{rcl} \theta&=&\arg\left(\alpha\right)\\&=&\arg\left(-\dfrac{1}{2}+\dfrac{1}{2}\vec{i}\right)\\&=&\dfrac{3\pi}{4}\left[2\pi\right] \end{array}$

Commentaire: si le candidat

$-\ $précise que $A$ est le point invariant de l'application qui à $M((z)\mapsto M'\left(z'\right)$

$-\ $puis,pour tout $M\neq A$ ,détermine le rapport $\dfrac{AM'}{AM'}$

$-\ $ensuite,une mesure de l'angle $\left(\overrightarrow{AM}\;,\overrightarrow{AM'}\right)$

alors i la répondu a la question.

Vous lui donnez

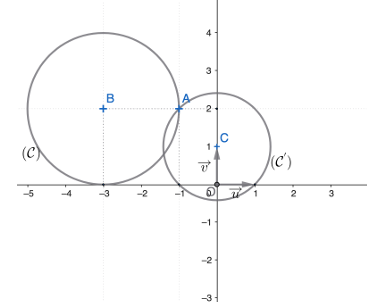
c. Soit le cercle $(C)$ d'équation $\left(x+3\right)^{2}+\left(y-2\right)^{2}=4$

Déterminons l'équation de $(C')$, image par $S$ de $(C)$

On considère l'expression analytique de $S$

$\left\lbrace\begin{array}{rcl} x'&=&-\dfrac{1}{2}x-\dfrac{1}{2y}-\dfrac{1}{2}\quad \left(E_{1}\right)\\
y'&=&\dfrac{1}{2}x-\dfrac{1}{2}y+\dfrac{7}{2}\quad\left(E_{2}\right) \end{array}\right.$

Exprimons $x$ et $y$ en fonction de $x'$ et $y'$

$\begin{array}{rcl} \left(E_{1}\right)+\left(E_{2}\right)&\Longleftrightarrow&x'+y'\\&=&-y+3\\&\Longleftrightarrow&y\\&=&-x'-y'+3 \end{array}$

$\begin{array}{rcl} \left(E_{1}\right)-\left(E_{2}\right)&\Longleftrightarrow&x'-y'\\&=&-x-4\\&\Longleftrightarrow&x\\&=&-x'+y'-4 \end{array}$

$\begin{array}{rcl} (x+3)^{2}+(y-2)^{2}&=&4\\&\Longleftrightarrow&\left(-x'-y'-4+3\right)^{2}+\left(-x'-y'+3-2\right)\\&=&4 \end{array} $

$\begin{array}{rcl} &\Longleftrightarrow&\left(-x'+y'-1\right)^{2}+\left(-x'-y'+1\right)^{2}\\&=&4\\&\Longleftrightarrow&\left[\left(-x'+y'\right)-1\right]^{2}+\left[\left(-x'-y'\right)+1\right]^{2}\\&=&4
\end{array}$

$\begin{array}{rcl} &\Longleftrightarrow&\left(x'\right)^{2}-2x'y'+\left(y'\right)+2x'-2y'+1+\left(x'\right)^{2}+2x'y'+\left(y'\right)^{2}-2x'-2y'+1\\&=&4 \end{array}$

$\begin{array}{rcl} &\Longleftrightarrow&c2\left(x'\right)^{2}+2\left(y'\right)^{2} -4y'\\&=&2\\&\Longleftrightarrow&\left(x'\right)^{2}+\left(y'\right)^{2}-2y'\\&=&1 \end{array}$

$\begin{array}{rcl} &\Longleftrightarrow&\left(x'\right)^{2}+\left(y'-1\right)^{2}-1\\&=&1 \end{array}$

$\begin{array}{rcl}&\Longleftrightarrow&\left(x'\right)^{2}+\left(y'-1\right)^{2}\\&=&2 \end{array}$

$\left(C'\right)$, l'image de $(C)$ par $S$, est le cercle d'équation : $\left(x'\right)^{2}+\left(y'-1\right)^{2}=2$

Commentaire: si le candidat

$-\ $détermine le point $B$, image du centre $B$ de $(C)$ par $S$,

$-\ $ensuite,considère $M'\left(x'\;,y'\right)$ l' image d'un $M(x\;,y)\in(C)$,

$-\ $Puis,pose $B'M'=\dfrac{\sqrt{2}}{2}BM+\sqrt{2}$

pour déterminer l'équation du cercle $(C')$ de centre $B'$ et de rayons $\sqrt{2}$ alors vous lui donnez

d. Traçons $(C)$ et $(C')$ dans le repère

Exercice 2

Dans cet exercice, les outils mathématiques au programme de Terminale $S2$ utilises par l'élève
sont les Probabilités.

L'expérience aléatoire consiste a contrôler l'état des téléphones portables fabriques avant leur mise en vente.

On a une suite de preuves de Bernouilli.

Le preuve est répété en fois et n'a que deux issues :

le suces (tirer un téléphone non défectueux ) et l'échec (tirer un téléphone défectueux).

La probabilité du succès est $p$ et celle de l'échec est $q=1-p$

$P_{k}$ est la probabilité d'obtenir $k$ succès,donc $P_{k}=C_{n}^{k}P^{k}q^{n-k}$

1. Aidons le chef de l'usine a déterminer le nombre $n$ de téléphones a produire pour que la
chance d'obtenir au moins un téléphone défectueux soit supérieure ou égale a $0.999$

a. On sait que la probabilité d'avoir un téléphone défectueux est $q=\dfrac{1}{50}$ et celle d'avoir un téléphone non défectueux est $P=\dfrac{49}{50}$

Soit $A$ l'événement obtenir au moins un téléphone défectueux parmi le $n$ téléphones fabriques .
$$P\left(\overline{A}\right)=p^{n}=\left(\dfrac{49}{50}\right)^{n}$$ ;

D'où
$$\begin{array}{rcl} p(A)&=&1-\left(\overline{A}\right)\\&=&1-p^{n}\\&=&1-\left(\dfrac{49}{50}\right)^{n}
\end{array}$$

La probabilité d'obtenir au moins un téléphone défectueux soit supérieure ou égale a $0.999$ est
équivaut à $p(A)\geq 0.999$

$\begin{array}{rcl}p(A)\geq 0.999&\Longleftrightarrow&1-\left(\dfrac{49}{50}\right)^{2}\\&\geq&0.999\\&\Longleftrightarrow&1-0.999\\&\geq&\left(\dfrac{49}{50}\right)\\&\Longleftrightarrow&\left(\dfrac{49}{50}\right)^{n}\\&\leq&0.001\\&\Longleftrightarrow&\ln\left(\dfrac{49}{50}\right)^{n}\\&\leq&\ln0.001\\&\Longleftrightarrow&n\ln\left(\dfrac{49}{50}\right)^{n}\\&\leq&\ln0.001\\&\Longleftrightarrow&n\ln0.001\\&\Longleftrightarrow&n\\&geq&\dfrac{\ln 0.001}{\ln\dfrac{49}{50}}\\&\text{ Donc } n&\geq&342 \end{array}$

L'usine doit fabriquer au moins $342$ pour que la chance d'obtenir au moins un téléphone
défectueux soit supérieure ou égale à $0.999$

Grille de correction de la question : Les $3$ points seront distribues comme suit : si le candidat

$-\ $ identifie les formules des probabilités qu'il doit utiliser dans cette situation.

$-\ $respecte les étapes dans l'utilisation des formules des probabilités dans cette situation.

$-\ $fait correctement les calculs.

$-\ $utilise les propriétés exactes (propriétés de la fonction $\ln$, résolution d'inéquations du premier degré avec des coefficients négatifs, etc).

$-\ $produit des résultats conformes aux résultats attendus.

$-\ $produit un résultat en adéquation avec la démarche.

$-\ $présente clairement et proprement les résultats.

2. a. On sait que le nombre de téléphones défectueux $T_{D}$ lorsque l'usine a produit exactement
$342$ téléphones est égal à :
$$\begin{array}{rcl} T_{d}&=&342\times\dfrac{2}{100}\\&=&7 \end{array}$$

Donc le prix de vente $P_{v}$ de ces téléphones non défectueux est égal à

$\begin{array}{rcl} P_{v}&=&(342-7)\times 45000\\&=&15075000\text{FCF A} \end{array}$

b. On sait aussi que le prix de revient $Pr$ des téléphones produits est égal a $11970000$ FCFA

Et $\begin{array}{rcl} P_{v}-P_{r}&=&10.075.000\text{FCFA}-11970000\text{FCFA}\\&=&3.105.00\text{}FCFA
\end{array}$

Donc l'usine aura un bénéfice de $B=3.105.00$ FCFA après la vente des $342$ téléphones non défectueux.

L'usine tirera pro t de la production de ces $342$ téléphones.

Donc elle tirera profit dune production supérieure a $342$ ; le prix de revient ne change pas.

Grille de correction de cette question : Les $3$ points seront distribues comme suit : si le
candidat

$-\ $identifie les formules donnant le nombre de téléphones défectueux, leur prix de vente et
un bénéfice ou une perte de la production.

$-\ $respecte les étapes dans l'utilisation des formules dans cette partie.

$-\ $fait correctement les calculs.

$-\ $produit des résultats conformes aux résultats attendus.

$-\ $produit un résultat en adéquation avec la démarche.

$-\ $interprété correctement les résultats obtenus en indiquant ce que l'entreprise pourrait gagner ou perdre.

Problème

Commentaire : Dans les trois parties qui suivent, le correcteur doit tenir compte de la
démarche, du raisonnement et de la justesse des résultats dans l'appréciation des copies des élèves.

Partie A

Soit $g$ la fonction définie sur $[1\ ;\ +\infty[$ par $g(x)=1-x\ln x$

1. Montrons que $\forall x\in[1\ ;\ +\infty[$ par $g(x)=1-x\ln x$

$\begin{array}{rcl} g'(x)&=&-\left(\ln x+x\times \dfrac{1}{x}\right)\\&=&-\ln x-1 \end{array}$

$\begin{array}{rcl} x\in[1\ ;\ +\infty[&\Longrightarrow&x\geq 1\\&\Longleftrightarrow&\ln x\geq 0\\&\Longleftrightarrow&\ln x+1\>0\\&\Longleftrightarrow&-\ln x-1<0\\&\Longleftrightarrow&\forall x\in[1\ ;\ +\infty[\;,g'(x)<0 \end{array}$

2. Tableau de variation de $g$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow\;,+\infty}g(x)&=&\lim\limits_{x\longrightarrow+\infty}1-x\ln x\\&=&-\infty\;,\lim\limits_{x\longrightarrow+\infty}1-x\ln x\\&=&1 \end{array}$

$\begin{array}{|c|ccccc|} x&1&&\alpha&&+\infty\\ \hline g'(x)&&&-&&\\ \hline &1\diagdown&&&\\ g&&0\searrow\\
&&&&-\infty \end{array}$

3. Montrer que $g$ est une bijection de $[1\ ;\ +\infty[$ sur un intervalle a préciser.

$g$ est continue et strictement décroissante sur $[1\ ;\ +\infty[$, donc $g$ est une bijection de $[1\ ;\ +\infty[$ sur $g([1\ ;\ +\infty[)=]-\infty\ ;\ 1]$

4. Montrons que l'équation $g(x)=0$ admet une unique solution $\alpha$ dans $1\ ;\ +\infty[$

$g$ est une bijection de $[1\ ;\ +\infty[$ sur $]1\ ;\ +\infty[$

Or $0\in]-\infty\ ;\ 1]$ donc l'équation $g(x)=0$ admet une unique solution $\alpha$ dans $[1\ ;\ +\infty[$

5. Montrons que l'équation $1.7<\alpha<1.8$

$1.7\in[1\ ;\ +\infty[$ et

$1.8\in[1\ ;\ +\infty[$

$g(1.7)=1-1.7\ln 1.7\simeq 0.1$ ;

$g(1.8)=1-1.8\ln 1.8\simeq -0.06$

$g(1.7)\times g(1.8)<0$,

donc $1.7<\alpha < 1.8$

6. Signe de g sur $[1\ ;\ +\infty[$ :

D'après le tableau de variation, on a :

$g(x)>0\text{ si }x\in[1\ ;\ \alpha[$ ;

$g(x)<0\text{ si }x\in]]\alpha\ ;\ +\infty[$

$g(x)=0\Longleftrightarrow x=\alpha$

Partie B

Soit $f$ la fonction de nie par :

$f(x)=\left\lbrace\begin{array}{rcl} (-x+1)\ln(-x+1)&\text{ si }&x<1\\ \mathrm{e}^{-x+1}\ln x&\text{ Si }&x\geq 1 \end{array}\right.$

1.a $f(x)$ existe $\Longleftrightarrow\left\lbrace\begin{array}{rcl} x&<&1\\ -x+1&>&0 \end{array}\right.$

$\text{ ou }\left\lbrace\begin{array}{rcl} x&\geq& 1\\ x&>&0 \end{array}\right.$

$\Longleftrightarrow x< 1\text{ ou }1\Longleftrightarrow x\in\mathbb{R}$

Donc $D_{f}=\mathbb{R}$

b. Rappel des limites suivantes :

$\lim\limits_{x\longrightarrow+\infty}\dfrac{\ln x}{x}=0$ ;

$\lim\limits_{x\longrightarrow 1}\dfrac{\ln x}{x-1}=1$ ;

$\lim\limits_{x\longrightarrow \infty}\dfrac{\mathrm{e}^{x}}{\ln x}=+\infty$ ;

$\lim\limits_{x\longrightarrow -\infty}x\mathrm{e}^{x}=0$

c. Calculons $\lim\limits_{x\longrightarrow -\infty}f(x)$

Sur $\begin{array}{rcl} [1\ ;\ +\infty[\;,f(x)&=&\mathrm{e}^{-x+1}\ln x\\&=&\mathrm{e}^{-x}\times \mathrm{e}\ln x\\&=&\mathrm{e}\times \dfrac{\ln x}{\mathrm{e}^{x}} \end{array}$

Or $\lim\limits_{x\longrightarrow+\infty}\dfrac{\mathrm{e}^{x}}{\ln x}=+\infty$ par conséquent $\lim\limits_{x\longrightarrow+\infty}\dfrac{\ln x}{\mathrm{e}^{x}}=0$ ; $\lim\limits_{x\longrightarrow+\infty}f(x)=0$

$\lim\limits_{x\longrightarrow+\infty}\dfrac{\mathrm{e}^{x}}{\ln x}f(x)=0$, donc le droite d'équation $y=0$ est une asymptote horizontale à $\left(C_{f}\right)$ en $+\infty$

d. Branche infinie en $-\infty$ :

Pour $x<1$$, $\dfrac{f(x)}{x}=\dfrac{-x+1}{x}\ln(-x+1)$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow -\infty}\dfrac{-x+1}{x}&=&\lim\limits_{x\longrightarrow-\infty}\dfrac{-x}{x}\\&=&-1\ ;\ \lim\limits_{x\longrightarrow-\infty}\ln(-x+1)\\&=&+\infty\ ;\ \lim\limits_{x\longrightarrow -\infty}\dfrac{f(x)}{x}\\&=&-\infty\\;,,&\text{ donc }\left(C_{f}\right)
\end{array}$

admet une branche parabolique de direction l'axe des ordonnées en.

2.a.Continuité de $f$ en $1$ :

Posons $t=-x+1$

Alors $x\longrightarrow 1^{-}\Longleftrightarrow t\longrightarrow 0^{+}$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow 1^{-}}f(x)&=&\lim\limits_{x\longrightarrow 1^{-}}(-x+1)\ln(-x+1)\\&=&\lim\limits_{t\longrightarrow 0^{+}}t\ln t\\&=&0 \end{array}$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow 1^{+}}f(x)&=&\lim\limits_{x\longrightarrow 1^{+}}\mathrm{e}^{-x+1}\ln x\\&=&\mathrm{e}^{0}\ln 1\\&=&0 \end{array}$

$\begin{array}{rcl} f(1)&=&\mathrm{e}^{0}\ln 1\\&=& \end{array}$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow 1^{-}}&=&\lim\limits_{x\longrightarrow 1^{+}}f(x)\\&=&f(1)\\&=&0 \end{array}$,

donc $f$ est continue en $1$

b. Dérivabilité de $f$ en $1$

Supposons que $x<1$

Alors on a : $\begin{array}{rcl} \dfrac{f(x)-f(1)}{x-1}&=&\dfrac{(-x+1)\ln(-x+1)}{x-1}\\&=&\dfrac{-(x-1)\ln(-x+1)}{x-1} \end{array}$

D'où $\dfrac{f(x)-f(1)}{x-1}=-\ln(-x+1)$, pour tout $x<1$

La probabilité d'obtenir au moins un téléphone défectueux soit supérieure ou égale a $0.999$ est
équivaut à $p(A)\geq 0.999$

$\begin{array}{rcl}p(A)\geq 0.999&\Longleftrightarrow&1-\left(\dfrac{49}{50}\right)^{2}\\&\geq&0.999\\&\Longleftrightarrow&1-0.999\\&\geq&\left(\dfrac{49}{50}\right)\\&\Longleftrightarrow&\left(\dfrac{49}{50}\right)^{n}\\&\leq&0.001\\&\Longleftrightarrow&\ln\left(\dfrac{49}{50}\right)^{n}\\&\leq&\ln0.001\\&\Longleftrightarrow&n\ln\left(\dfrac{49}{50}\right)^{n}\\&\leq&\ln0.001\\&\Longleftrightarrow&n\n\ln0.001\\&\Longleftrightarrow&n\\&geq&\dfrac{\ln 0.001}{\ln\dfrac{49}{50}}\\&\text{ Donc } n&\geq&342 \end{array}$