Fonction exponentielle - TL

I. Étude de la fonction logarithme exponentielle

1. Définition et notation

La fonction exponentielle notée `$\exp$ est une fonction qui est définie et dérivable sur qui est égale à sa fonction dérivée et qui est strictement positive sur.

Autrement dit

$\bullet\ $L'ensemble de définition de la fonction exponentielle est et l'image de tout réel $x$par la fonction exponentielle est le réel strictement positif noté $\text{exp }x$

on lit exponentielle de $x.$

$\bullet\ $La fonction exponentielle est dérivable sur $\mathbb{R}$ et pour tout $x\in\mathbb{R}$, $\text{exp}'(x)=\text{exp }(x)$

2. Remarque

$\bullet\ $On admet que pour tout $x\in\mathbb{R}$, $\text{exp}(x)=\mathrm{e}^{x}$ où est l'unique réel strictement positif tel
que $\ln\mathrm{e}=1$ et dont une valeur approchée est $\mathrm{e}\cong 2.718$

$\bullet\ \mathrm{e}^{0}=1$ et $\mathrm{e}^{1}=\mathrm{e}$

3. Propriétés

i. Pour tout $\in\mathbb{R}$, $\mathrm{e}^{x}>0$

ii. Pour tout $x\in\mathbb{R}$, $\ln\left(\mathrm{e}^{x}\right)=x$

iii. Si $x<0$ alors on a : $\mathrm{e}^{\ln x}=x$

iv. Si $x>0$ et si $y\in\mathbb{R}$ alors on a : $\ln x=y\Longleftrightarrow\,x=\mathrm{e}^{y}$

Exercice d'application

1. Simplifier autant que possible le nombre suivant : $A=\ln\left(\mathrm{e}^{3}\right)+\mathrm{e}^{\ln 5}-\ln\left(\mathrm{e}^{2}\right)+\mathrm{e}^{\ln 3}$

2. Résoudre dans $\mathbb{R}$, les équations $\ln x=-2$ ; $\mathrm{e}^{x}=2$ et $(\ln x)^{2}-1=0$

4. Autres propriétés

$\mathrm{e}^{x+y}=\mathrm{e}^{x}\mathrm{e}^{y}$

$\mathrm{e}^{-x}=\dfrac{1}{\mathrm{e}^{x}}$

$\mathrm{e}^{x-y}=\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{y}}$

Si $r$ est un nombre rationnel alors on a : $\mathrm{e}^{rx}=\left(\mathrm{e}^{x}\right)^{r}$

5. Représentation graphique

Soit $f$ la fonction telle que $f(x)=\mathrm{e}^{x}$

a. limites aux bornes

$D_{f}=]-\infty\ ;\ +\infty[$

$\bullet\ $ $\begin{array}{rcl} \lim\limits_{x\longrightarrow\,-\infty}f(x)&=&\lim\limits_{x\longrightarrow\,-\infty}\mathrm{e}^{x}\\&=&0 \end{array}$

$\bullet\ $ $\begin{array}{rcl}\lim\limits_{x\longrightarrow\,-\infty}f(x)&=&\lim\limits_{x\longrightarrow\,+\infty}\mathrm{e}^{x}\\&=&+\infty \end{array}$

b. Branches infinies

$\bullet\ $$\lim\limits_{x\longrightarrow\,-\infty}\mathrm{e}^{x}=0$ donc la droite d'équation $y=0$ (l'axe des abscisses) est une asymptote horizontale de $C_{f}$ en $-\infty$

$\bullet\ $ $\lim\limits_{x\longrightarrow\,+\infty}\dfrac{\mathrm{e}^{x}}{x}=+\infty$ donc l'axe des ordonnées est une branche parabolique de $C_{f}$ en $+\infty$

c. Dérivée et sens de variation

$f$ est dérivable sur et pour tout $x\in\mathbb{R}\,f'(x)=\mathrm{e}^{x}$

Or pour tout $x\in\mathbb{R}\;,\mathrm{e}^{x}>0$  donc $f'(x)>0$ d'où $f$ est strictement croissante sur $\mathbb{R}$

d. Tableau de variation

Le tableau suivant est celui des variations de  $f$

$\begin{array}{|c|cccc|} \hline x & -\infty & & & +\infty \\ \hline \exp'(x) & & + & & \\\hline         &  &         & &  +\infty \\ \exp(x)  &  & \nearrow &  & \\         & 0 &        &  &  \\ \hline \end{array}$

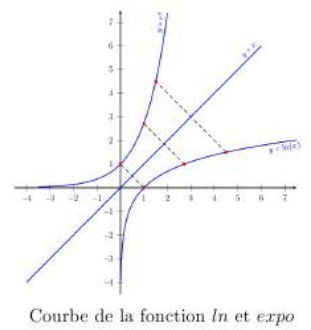
e. Courbe représentative de la fonction exponentielle

$\bullet\ $Équations des tangentes aux points d'abscisses $0$ et $1$

L'équation de la tangente $(T)$ à $C_{f}$ au point d'abscisse $0$ est $\begin{array}{rcl} (T)\ :\ y&=&f'(0)(x-0)+f(0)\\&=&x+1 \end{array}$

L'équation de la tangente $\left(T'\right)$ à $C_{f}$ au point d'abscisse $1$

$\begin{array}{rcl} \left(T'\right)\ :\ y&=&f'(1)(x-1)+f(1)\\&=&\mathrm{e}(x-1)+\mathrm{e}\\&=&\mathrm{e}x\end{array}$

Tableau de valeurs

$$\begin{array}{|c|c|c|c|c|} \hline x&0&1&2&2.5\\ \hline f(x)&1&\mathrm{e}&7.4&12\\ \hline \end{array}$$

$\bullet\ $

II. Équations et inéquations faisant intervenir la fonction exponentielle

1. Équations

$\bullet\ $Propriétés

Si $x$ et $y\in\mathbb{R}$ alors $\mathrm{e}^{x}=\mathrm{e}^{y}\Longleftrightarrow\, x=y$

$\bullet\ $Équations du type $\mathrm{e}^{u(x)}=\mathrm{e}^{v(x)}$
 
Si $u(x)$ et $v(x)$ sont des expressions bien définies alors on a $\begin{array}{rcl} \mathrm{e}^{u(x)}&=&\mathrm{e}^{v(x)}\\&\Longrightarrow&u(x)\\&=&v(x) \end{array}$

Exemple : Résolvons dans $\mathbb{R}$ les équations suivantes :

$\mathrm{e}^{x-2}=\mathrm{e}^{-x+3}$ et $\mathrm{e}^{x^{2}}=\mathrm{e}^{-x+6}$

2. Inéquations

$\bullet\ $Propriétés : Soient $x$ et $y\in\mathbb{R}$

i. $\mathrm{e}^{x}\geq\mathrm{e}^{y}\Leftrightarrow\, x\geq y$

ii. $\mathrm{e}^{x}\leq \mathrm{e}^{y}\Leftrightarrow\, x\leq y$

iii. $\mathrm{e}^{x}\leq y(y>0)\Leftrightarrow\,x\leq \ln y$

iv. $\mathrm{e}^{x}\geq y(y>0)\Leftrightarrow\,x\geq \ln y$

NB : Les inégalités strictes ci-dessus peuvent être larges.

$\bullet\ $ Exemple : Résoudre dans les inéquations suivantes

i. $\mathrm{e}^{-2x+1}\leq \mathrm{e}^{-4x+6}$

ii. $\mathrm{e}^{x}\geq 5$

III. Fonction comportant l'exponentielle

1. Limites

a. Limite usuelle

$\lim\limits_{x\longrightarrow\,-\infty}x\mathrm{e}^{x}=0$

b. Autre limites

Pour calculer $\lim\limits_{x\longrightarrow\,\alpha}\mathrm{e}^{u(x)}$, on calcule d'abord $\lim\limits_{x\longrightarrow\,\alpha}u(x)$ :

i. Si $\lim\limits_{x\longrightarrow\,\alpha}u(x)=l$ où $l\in\mathbb{R}$ alors $\lim\limits_{x\longrightarrow\,\alpha}\mathrm{e}^{u(x)}=\mathrm{e}^{l}$

ii. Si $\lim\limits_{x\longrightarrow \alpha}u(x)=-\infty$ alors $\lim\limits_{x\longrightarrow\,\alpha}\mathrm{e}^{u(x)}=0$