Correction Serie d'exercices : Fonction exponentielle- TL

Exercice 1  

 
$$A = \frac{e^{5x} \times e^{-2x}}{e^{-x+2}} = \frac{e^{5x-2x}}{e^{-x+2}} = e^{5x-2x+x-2} = e^{4x-2}$$  

Exercice 2  

1. $(E)$ équivaut à $x(e^x-1) = 0$, donc $x = 0$ ou $e^x = 1$.  
   Solution : $S_{\mathbb{R}} = \{ 0 \}$.  

2. Tableau de signes pour $(I)$:  

$$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -\infty & -2 & 0 & 1 & +\infty \\ \hline x^2 + x - 2 & + & - & - & + & + \\ \hline e^{2x} - 1 & - & - & 0 & + & + \\ \hline f(x) & - & + & \big| & - & + \\ \hline \end{array}$$

Solution : $S_{\mathbb{R}} = [-2; 0[ \cup [1; +\infty[$.  

Exercice 3 : Dérivation

a) $f(x) = e^{-2x+1}$

$$f'(x) = e^{-2x+1} \cdot (-2)$$

 $f'(x) = -2e^{-2x+1}$

b) $f(x) = x + 2 - e^x$

$$f'(x) = 1 - e^x$$

 $f'(x) = 1 - e^x$

c) $f(x) = (1 - x)e^x$
Produit : $u(x) = 1 - x, \quad v(x) = e^x$

$$f'(x) = u'v + uv' = (-1)e^x + (1 - x)e^x = (1 - x - 1)e^x = -x e^x$$

 $f'(x) = -x e^x$

Exercice 4 : Limites

a) $f(x) = (2x+1)e^x + \frac{1}{x}$, $x \to +\infty$

 $(2x+1)e^x \to +\infty$
 $\frac{1}{x} \to 0$

 Limite : $+\infty$

b) $f(x) = 2 \cdot \frac{e^x - 1}{x} + x^2$, $x \to 0$

 Utiliser $\lim_{x \to 0} \frac{e^x - 1}{x} = 1$

$$\lim_{x \to 0} f(x) = 2 \cdot 1 + 0 = 2$$

 Limite : $2$

Exercice 5 : Primitives

a) $f(x) = e^{4x} \Rightarrow \int e^{4x} dx = \frac{1}{4}e^{4x} + C$
     Primitive: $F(x) = \frac{1}{4} e^{4x}$

b) $\int e^{3x} dx = \frac{1}{3}e^{3x}, \quad \int e^{-\frac{1}{2}x} dx = -2e^{-\frac{1}{2}x}, \quad \int 5dx = 5x$

 Primitive : $F(x) =\frac{1}{3}e^{3x} + 2e^{-\frac{1}{2}x} + 5x$

c) $\int (x - \frac{3}{4}) dx + \int 3e^{-2x+1} dx$

 $\int x dx = \frac{x^2}{2}, \int -\frac{3}{4} dx = -\frac{3}{4}x$
 $\int 3e^{-2x+1} dx = -\frac{3}{2}e^{-2x+1}$

 Primitive : $F(x) =\frac{x^2}{2} - \frac{3}{4}x - \frac{3}{2}e^{-2x+1}$

Exercice 6 : QCM

1.

$\dfrac{e^{2x} - e^x}{e^x + 1} = \dfrac{e^x(e^x - 1)}{e^x + 1} = \boxed{\text{Réponse B}}$

2.

$x^2 - x - 1 = 3x - 4 \Rightarrow x^2 - 4x + 3 = 0 \Rightarrow x = 1 \text{ ou } x = 3 \Rightarrow \boxed{\text{Réponse C}}$

3.

$e^x - 2x \to +\infty$ car $e^x \gg 2x \Rightarrow \boxed{\text{Réponse A}}$

4.

$f(x) = xe^{-2x} \Rightarrow f'(x) = e^{-2x} + x(-2e^{-2x}) = (1 - 2x)e^{-2x} \Rightarrow \boxed{\text{Réponse C}}$

Exercice 7  

 a)
    $(e^{2x})^{2} \times (e^{x})^{2} = e^{4x} \times e^{-2x} = e^{4x - 2x} = e^{2x}$
    
  b)
    $(e^{x} + e^{-x})^{2} - (e^{x} - e^{-x})^{2} = (e^{x} + e^{-x} - e^{x} + e^{-x})(e^{x} + e^{-x} + e^{x} - e^{-x})= (2e^{-x})(2e^{x}) = 4e^{-x}e^{x} = 4$
    

Exercice 8  

• Signe de B

$$B = e^{2x} + e^x - 2$$

Posons $e^x = X$, donc $X > 0$. On a $X^2 + X - 2$.

$$\Delta = 1 + 8 = 9$$
$$X = -2 \quad \text{ou} \quad X = 1$$

Étudions le signe de $X^2 + X - 2$.

$$\begin{array}{|c|ccccc|} \hline  X &  -\infty &  -2 &  1 &  +\infty \\ \hline  X^2 + X - 2 &  + &  0 &  - &  0 &  + \\ \hline \end{array}$$

$X^2 + X - 2 \geq 0 \iff X \in ]-\infty; -2] \cup [1; +\infty[$

On a : $e^x \in ]-\infty; -2]$ ou : $e^x \in [1; +\infty[$

$e^x \leq -2$ est impossible ou $e^x \geq 1$ équivaut à $x \geq \ln 1$

Pour $x \in [0; +\infty[$, $e^{2x} + e^x - 2 > 0$

Pour $x \in ]-\infty; 0]$, $e^{2x} + e^x - 2 < 0$

• Signe de C}

$$C = e^x - 2e^{-x} + 1 = \frac{e^{2x} + e^x - 2}{e^x}$$

Comme pour $x \in \mathbb{R}$, $e^x > 0$ donc le signe de C est le même que celui de B.

Exercice 9 : Déterminer les limites en $+\infty$ et $-\infty$

 a) $f(x) = \dfrac{e^{x+1}}{e^x + 2}$

Limite en $+\infty$ :

Quand $x \to +\infty$, $e^x$ domine, donc le dénominateur $e^x + 2 \approx e^x$.

Ainsi :
$$f(x) \approx \dfrac{e^{x+1}}{e^x} = e^{x+1 - x} = e^1 = e$$

Donc :
$$\lim_{x \to +\infty} f(x) = e$$

Limite en $-\infty$ :

Quand $x \to -\infty$, $e^x \to 0$, donc :
$$f(x) \approx \dfrac{e^{x+1}}{0 + 2} = \dfrac{e^{x+1}}{2} \to 0$$

Donc :
$$\lim_{x \to -\infty} f(x) = 0$$

 b) $f(x) = \dfrac{x e^x}{x + 1}$

Limite en $+\infty$ :

Quand $x \to +\infty$, $e^x$ croît beaucoup plus vite que $x$, donc le numérateur $x e^x$ domine le dénominateur $x + 1 \approx x$.

Ainsi :
$$f(x) \approx \dfrac{x e^x}{x} = e^x \to +\infty$$

Donc :
$$\lim_{x \to +\infty} f(x) = +\infty$$

Limite en $-\infty$ :

Quand $x \to -\infty$, $e^x \to 0$, et le dénominateur $x + 1 \to -\infty$.

Le numérateur $x e^x$ est le produit de $x \to -\infty$ et $e^x \to 0$. On a une forme indéterminée $-\infty \times 0$.

Réécrivons $f(x)$ :
$$f(x) = \dfrac{x e^x}{x + 1} = \dfrac{x}{x + 1} \cdot e^x$$

Quand $x \to -\infty$, $\dfrac{x}{x + 1} \to 1$ (car $\dfrac{x}{x(1 + 1/x)} = \dfrac{1}{1 + 1/x} \to 1$).

Donc :
$$f(x) \approx 1 \cdot e^x \to 0$$

Donc :
$$\lim_{x \to -\infty} f(x) = 0$$

c)
Pour déterminer les limites de la fonction $f(x) = \dfrac{e^{x} + 1}{e^x + 2}$ en $+\infty$ et en $-\infty$, nous allons analyser séparément chaque cas.

 1. Limite en $+\infty$ :

Quand $x \to +\infty$, $e^x$ tend vers $+\infty$. On peut factoriser $e^x$ au numérateur et au dénominateur :

$$f(x) = \dfrac{e^{x} + 1}{e^x + 2} = \dfrac{e^x \left(1 + \dfrac{1}{e^x}\right)}{e^x \left(1 + \dfrac{2}{e^x}\right)} = \dfrac{1 + \dfrac{1}{e^x}}{1 + \dfrac{2}{e^x}}$$

Quand $x \to +\infty$, $\dfrac{1}{e^x} \to 0$ et $\dfrac{2}{e^x} \to 0$. Ainsi :

$$\lim_{x \to +\infty} f(x) = \dfrac{1 + 0}{1 + 0} = 1$$

Conclusion :  
$$\boxed{ \lim_{x \to +\infty} \dfrac{e^{x} + 1}{e^x + 2} = 1 }$$

 2. Limite en $-\infty$ :

Quand $x \to -\infty$, $e^x$ tend vers $0$. On a donc :

$$f(x) = \dfrac{e^{x} + 1}{e^x + 2} \approx \dfrac{0 + 1}{0 + 2} = \dfrac{1}{2}$$

Conclusion :  
$$\boxed{ \lim_{x \to -\infty} \dfrac{e^{x} + 1}{e^x + 2} = \dfrac{1}{2} }$$

Exercice 10 : Trouver une primitive de $f$ sur $\mathbb{R}$

 a) $f(x) = e^{3x} - e^{-\dfrac{1}{2}x} + 5$

On intègre terme à terme :

1. $\int e^{3x} \, dx = \dfrac{1}{3} e^{3x} + C$
2. $\int -e^{-\dfrac{1}{2}x} \, dx = -\left( \dfrac{1}{-1/2} e^{-\dfrac{1}{2}x} \right) + C = 2 e^{-\dfrac{1}{2}x} + C$
3. $\int 5 \, dx = 5x + C$

Une primitive $F$ de $f$ est donc :
$$F(x) = \dfrac{1}{3} e^{3x} + 2 e^{-\dfrac{1}{2}x} + 5x + C$$
(où $C$ est une constante réelle).

 b) $f(x) = \dfrac{e^{2x}}{1 + e^{2x}}$

On reconnaît une forme $\dfrac{u'}{u}$, où $u = 1 + e^{2x}$ et $u' = 2 e^{2x}$.

Ainsi :
$$f(x) = \dfrac{e^{2x}}{1 + e^{2x}} = \dfrac{1}{2} \cdot \dfrac{2 e^{2x}}{1 + e^{2x}} = \dfrac{1}{2} \cdot \dfrac{u'}{u}$$

Donc une primitive est :
$$F(x) = \dfrac{1}{2} \ln|u| + C = \dfrac{1}{2} \ln(1 + e^{2x}) + C$$
(On peut omettre la valeur absolue car $1 + e^{2x} > 0$).

 c) $f(x) = (2x - 3) e^{-x^2 + 3x + 1}$

On reconnaît une forme $u' e^u$, où $u = -x^2 + 3x + 1$ et $u' = -2x + 3$.

Ajustons le coefficient :
$$2x - 3 = -(-2x + 3) = -u'$$

Ainsi :
$$f(x) = (2x - 3) e^{u} = -u' e^{u}$$

Une primitive de $u' e^{u}$ est $e^{u}$, donc une primitive de $-u' e^{u}$ est $-e^{u}$.

Donc :
$$F(x) = -e^{-x^2 + 3x + 1} + C$$

Exercice 11  

1. L'ensemble de définition de $f$ est $D_f = \mathbb{R}$.

2.
$$\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} (1 - x + e^x) = +\infty, \quad \text{car } \lim_{x \to -\infty} -x = +\infty, \quad \lim_{x \to -\infty} e^x = 0.$$

3.
    
    a) Pour tout nombre réel $x \neq 0$,
    $$f(x) = 1 - x + e^x = x \left( \frac{1}{x} - 1 + \frac{e^x}{x} \right).$$
    b)
    $$f(x) = 1 - x + e^x, \quad \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \left( x \left( \frac{1}{x} - 1 + \frac{e^x}{x} \right) \right).$$
    Comme $\lim_{x \to +\infty} \frac{1}{x} = 0$, $\lim_{x \to +\infty} \frac{e^x}{x} = +\infty$, on a
    $$\lim_{x \to +\infty} f(x) = +\infty.$$
4.  a)
    $$\lim_{x \to -\infty} \left( f(x) - (-x + 1) \right) = \lim_{x \to -\infty} e^x = 0.$$
    Donc la droite $(\Delta)$ d'équation $y = -x + 1$ est asymptote oblique à $(C)$ en $-\infty$.

   b) On a :
    $$f(x) - (-x + 1) = e^x,$$
    donc le signe de $f(x) - (-x + 1)$ est celui de $e^x$; or pour tout réel $x$, $e^x > 0$, par suite $(C)$ est au-dessus de $(\Delta)$ sur $\mathbb{R}$.

5.

    a) Pour tout élément $x$ de $\mathbb{R}$,
    $$f'(x) = -1 + e^x.$$
    b)
    $$f'(x) = 0 \iff -1 + e^x = 0 \iff e^x = 1 \iff x = 0.$$
    c)
    $$f'(x) > 0 \iff -1 + e^x > 0 \iff e^x > 1 \iff x > 0.$$
    d) Pour tout $x > 0$, $f'(x) > 0$, donc $f$ est strictement croissante sur $]0; +\infty[$.\\
    Pour tout $x < 0$, $f'(x) < 0$, donc $f$ est strictement décroissante sur $]-\infty; 0[$.

$$\begin{array}{|c|c|c|c|} \hline x & -\infty & 0 & +\infty \\ \hline f'(x) & - & 0 & + \\ \hline f(x) & \searrow & 2 & \nearrow \\ \hline \end{array}$$

6. Tableau de valeurs :  

   $$\begin{array}{|c|c|c|c|c|c|c|}    \hline    x & -3 & -2 & -1 & 0 & 1 & 2 \\    \hline    f(x) & 4,05 & 3,39 & 2,39 & 2 & 2,78 & 6,59 \\    \hline    \end{array}$$  

7. Représentation graphique :  
   - Tracer $C$ et $\Delta$ sur $[-3; 2]$.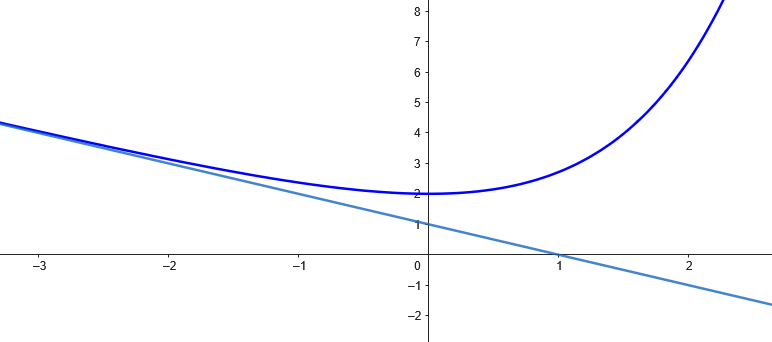 

Exercice 12  

Soit $f(x) = (-2x + 3) e^x$ définie sur $]-\infty; 2]$.  

1. Limite en $-\infty$ :  
   $$\lim_{x \to -\infty} f(x) = 0 \quad \text{car} \quad \lim_{x \to -\infty} (-2x + 3) e^x = 0.$$  
   - Interprétation : La droite $y = 0$ est asymptote horizontale en $-\infty$.  

2. Dérivée et variations :  
   - $f'(x) = (-2x + 1) e^x$.  
   - Signe de $f'(x)$ :  
     - $f'(x) > 0$ pour $x < \frac{1}{2}$.  
     - $f'(x) < 0$ pour $x > \frac{1}{2}$.  
   - Tableau de variations :  

$$\begin{array}{|c|c|c|c|} \hline x & -\infty & \frac{1}{2} & 2 \\ \hline f'(x) & + & 0 & - \\ \hline f(x) & \nearrow & 3,3 &  \searrow\\ \hline \end{array}$$

3. Points d'intersection :  
   - Avec l'axe des abscisses ($A$) :  
     $$(-2x + 3) e^x = 0 \implies x = \frac{3}{2}, \quad A\left( \frac{3}{2}, 0 \right).$$  
   - Avec l'axe des ordonnées ($B$) :  
     $$f(0) = 3, \quad B(0, 3).$$  

4. Tableau de valeurs :  

   $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}    \hline    x & -4 & -3 & -2 & -1 & 0 & 0,5 & 1 & 1,5 & 2 \\    \hline    f(x) & 0,2 & 0,4 & 0,9 & 1,8 & 3 & 3,3 & 2,7 & 0 & -7,4 \\    \hline    \end{array}$$  

5. Représentation graphique :  
   - Tracer $C$ sur $]-\infty; 2]$.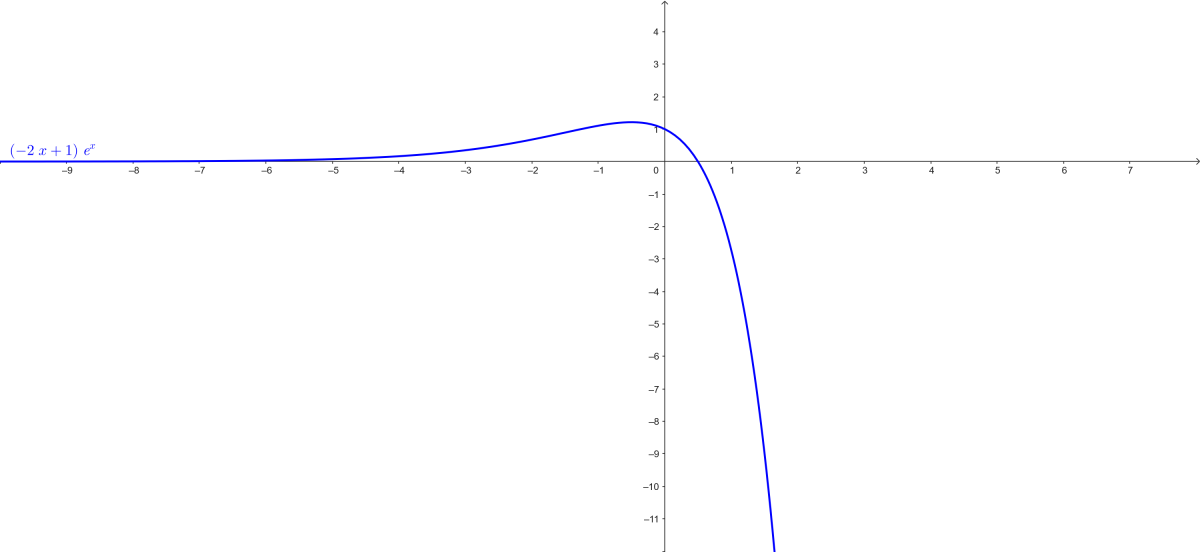  

EXERCICE 13

 1) Résoudre $e^{2x+1} = e^{3x+7}$
Les exponentielles sont égales si et seulement si leurs exposants sont égaux :
$$2x + 1 = 3x + 7\Leftrightarrow -x = 6\Leftrightarrow x = -6$$
 $\boxed{S=\{-6\}}$

 2) Résoudre $e^{-x+17} = e^x$
Égalité des exposants :
$$-x + 17 = x\Leftrightarrow 17 = 2x\Leftrightarrow x = \frac{17}{2}$$
 $\boxed{S=\{ \dfrac{17}{2}\}}$

 3) Résoudre $e^{x+3} \times e^{x-2} = e^3$
On combine les exponentielles :
$$e^{(x+3) + (x-2)} = e^3\Leftrightarrow e^{2x + 1} = e^3$$
Égalité des exposants :
$$2x + 1 = 3\Leftrightarrow 2x = 2\Leftrightarrow x = 1$$
 $\boxed{ S=\{1\} }$

 4) Résoudre $e^{2x} - 4e^x + 3 = 0$
Posons $y = e^x$ :
$$y^2 - 4y + 3 = 0\Leftrightarrow (y - 1)(y - 3) = 0\Leftrightarrow y = 1 \text{ ou } y = 3$$
Donc :
$$e^x = 1\Leftrightarrow x = 0 \quad \text{ou} \quad e^x = 3\Leftrightarrow x = \ln 3$$
 $\boxed{S=\{ 0 ; \ln 3\} }$

 5) Résoudre $e^{2(x+1)} - 8e^{x+2} - 9e^2 = 0$
Simplifions :
$$e^{2x + 2} - 8e^{x + 2} - 9e^2 = 0\Leftrightarrow e^2(e^{2x} - 8e^x - 9) = 0$$
Comme $e^2 \neq 0$, on a :
$$e^{2x} - 8e^x - 9 = 0$$
Posons $y = e^x$ :
$$y^2 - 8y - 9 = 0\Leftrightarrow (y - 9)(y + 1) = 0\Leftrightarrow y = 9 \text{ ou } y = -1$$
Seule $y = 9$ est possible car $e^x > 0$ :
$$e^x = 9\Leftrightarrow x = \ln 9 = 2 \ln 3$$
 $\boxed{S=\{2 \ln 3\}}$

 6) Résoudre $2e^{2x-4} + 5e^{x-2} - 3 = 0$
Posons $z = e^{x-2}$ :
$$2z^2 + 5z - 3 = 0\Leftrightarrow z = \frac{-5 \pm \sqrt{25 + 24}}{4} = \frac{-5 \pm 7}{4}$$
Donc $z = \frac{1}{2}$ ou $z = -3$. Seule $z = \frac{1}{2}$ est possible :
$$e^{x-2} = \frac{1}{2}\Leftrightarrow x - 2 = -\ln 2\Leftrightarrow x = 2 - \ln 2$$
 $\boxed{S=\{2 - \ln 2\}}$

 

EXERCICE 14

 1) Résoudre $e^{3x+2} \leq e$
L'exponentielle est croissante, donc :
$$3x + 2 \leq 1\Leftrightarrow 3x \leq -1\Leftrightarrow x \leq -\frac{1}{3}$$
 $\boxed{S=\left]-\infty, -\dfrac{1}{3}\right]}$

 2) Résoudre $e^x - 7 < 0$
$$e^x < 7\Leftrightarrow x < \ln 7$$
 $\boxed{S=\left]-\infty, \ln 7\right[}$

 3) Résoudre $e^{2x} - 9 > 0$
$$e^{2x} > 9\Leftrightarrow 2x > \ln 9\Leftrightarrow x > \ln 3$$
 $\boxed{S=\left]\ln 3, +\infty\right[}$

 4) Résoudre $e^x + 1 > 0$
Toujours vrai car $e^x > 0$.
 $\boxed{S=\mathbb{R}}$

 5) Résoudre $e^x(e^x - 4) < 0$
Posons $y = e^x$ :
$$y(y - 4) < 0\Leftrightarrow 0 < y < 4$$
Donc :
$$0 < e^x < 4\Leftrightarrow x < \ln 4$$
 $\boxed{S=\left]-\infty, \ln 4\right[}$

 6) Résoudre $e^{2x} + e^x - 6 \leq 0$
Posons $y = e^x$ :
$$y^2 + y - 6 \leq 0\Leftrightarrow (y + 3)(y - 2) \leq 0$$
Le trinôme est négatif entre ses racines $y = -3$ et $y = 2$. Seul $y \in [0, 2]$ est possible :
$$0 \leq e^x \leq 2\Leftrightarrow x \leq \ln 2$$
 $\boxed{S=\left]-\infty, \ln 2\right]}$

 7) Résoudre $e^{2x} + e^x - 2 \geq 0$
Posons $y = e^x$ :
$$y^2 + y - 2 \geq 0\Leftrightarrow (y + 2)(y - 1) \geq 0$$
Le trinôme est positif pour $y \leq -2$ ou $y \geq 1$. Seul $y \geq 1$ est possible :
$$e^x \geq 1\Leftrightarrow x \geq 0$$
 $\boxed{S=\left[0, +\infty\right[}$

EXERCICE 15

 1) Résoudre $e^{2x} + e^x + 1 = 0$
Posons $y = e^x$ :
$$y^2 + y + 1 = 0\Leftrightarrow \Delta = -3 < 0\Leftrightarrow \text{Aucune solution réelle.}$$
 $\boxed{S=\varnothing}$

 2) Résoudre $e^x - 13e^x - 48 = 0$
Cette équation semble incorrecte (peut-être $e^{2x} - 13e^x - 48 = 0$). Supposons :
$$e^{2x} - 13e^x - 48 = 0$$
Posons $y = e^x$ :
$$y^2 - 13y - 48 = 0\Leftrightarrow y = \frac{13 \pm \sqrt{169 + 192}}{2} = \frac{13 \pm 19}{2}$$
Donc $y = 16$ ou $y = -3$. Seule $y = 16$ est possible :
$$e^x = 16\Leftrightarrow x = \ln 16 = 4 \ln 2$$
 $\boxed{S=\{4 \ln 2\}}$

 3) Résoudre $2e^{2x} + 5e^x + 8 = 0$
Posons $y = e^x$ :
$$2y^2 + 5y + 8 = 0\Leftrightarrow \Delta = -39 < 0\Leftrightarrow \text{Aucune solution réelle.}$$
 $\boxed{S=\varnothing}$

 4) Résoudre $2e^{2x} + 4e^x + 2 = 0$
Posons $y = e^x$ :
$$2y^2 + 4y + 2 = 0\Leftrightarrow y^2 + 2y + 1 = 0\Leftrightarrow (y + 1)^2 = 0\Leftrightarrow y = -1$$
Aucune solution car $e^x > 0$.
 $\boxed{S=\varnothing}$

 5) Résoudre $e^x - e^x - 6 = 0$
Cette équation semble incorrecte (peut-être $e^{2x} - e^x - 6 = 0$). Supposons :
$$e^{2x} - e^x - 6 = 0$$
Posons $y = e^x$ :
$$y^2 - y - 6 = 0\Leftrightarrow y = 3 \text{ ou } y = -2$$
Seule $y = 3$ est possible :
$$e^x = 3\Leftrightarrow x = \ln 3$$
 $\boxed{S=\{\ln 3\}}$

 

EXERCICE 16

 1) Calculer $P(1)$ et factoriser $P(x)$
$$P(1) = 1 - 1 - 4 + 4 = 0\Leftrightarrow (x - 1) \text{ est un facteur.}$$
Division polynomiale ou identification :
$$P(x) = (x - 1)(x^2 - 4) = (x - 1)(x - 2)(x + 2)$$

 2) Résoudre $P(x) = 0$
$$(x - 1)(x - 2)(x + 2) = 0\Leftrightarrow x = 1, 2, -2$$

 3) Résolution des équations liées

a) $(\ln x)^3 - (\ln x)^2 - 4 \ln x + 4 = 0$
Posons $y = \ln x$ :
$$y^3 - y^2 - 4y + 4 = 0\Leftrightarrow (y - 1)(y - 2)(y + 2) = 0\Leftrightarrow y = 1, 2, -2$$
Donc :
$$\ln x = 1\Leftrightarrow x = e \\ \ln x = 2\Leftrightarrow x = e^2 \\ \ln x = -2\Leftrightarrow x = e^{-2}$$
 $\boxed{S=\{e^{-2}; e; e^2\}}$

b) $e^{3x} - e^{2x} - 4e^x + 4 = 0$
Posons $y = e^x$ :
$$y^3 - y^2 - 4y + 4 = 0\Leftrightarrow (y - 1)(y - 2)(y + 2) = 0\Leftrightarrow y = 1, 2, -2$$
Seules $y = 1$ et $y = 2$ sont possibles :
$$e^x = 1\Leftrightarrow x = 0 \\ e^x = 2\Leftrightarrow x = \ln 2$$
 $\boxed{S=\{0 ;\ln 2\}}$

c) $e^{3x} - e^{2x} - 4e^x + 4 \geq 0$
Posons $y = e^x$ :
$$(y - 1)(y - 2)(y + 2) \geq 0$$
Étude du signe :
- Pour $y \in ]-2, 1[$ : négatif
- Pour $y \in ]1, 2[$ : positif
- Pour $y > 2$ : positif

Seuls $y \in [1, 2]$ et $y \geq 2$ sont possibles :
$$1 \leq e^x \leq 2\Leftrightarrow 0 \leq x \leq \ln 2 \\ e^x \geq 2\Leftrightarrow x \geq \ln 2$$
 $\boxed{S=[0, +\infty[}$

 

EXERCICE 17

 1) Calculer $h(-2)$ et résoudre $h(x) = 0$
$$h(-2) = 2(-8) - 4 - 8(-2) + 4 = -16 - 4 + 16 + 4 = 0\Leftrightarrow (x + 2) \text{ est un facteur.}$$
Factorisation :
$$h(x) = (x + 2)(2x^2 - 5x + 2)$$
Résolution de $2x^2 - 5x + 2 = 0$ :
$$x = \frac{5 \pm \sqrt{25 - 16}}{4} = \frac{5 \pm 3}{4}\Leftrightarrow x = 2 \text{ ou } x = \frac{1}{2}$$
Donc :
$$h(x) = (x + 2)(x - 2)(2x - 1)$$
Solutions $S$ de $h(x) = 0$ : $\boxed{\{-2;\dfrac{1}{2};2\}}$

Résolution de $h(x) > 0$ :
Étude du signe :
- Pour $x < -2$ : négatif
- Pour $-2 < x < \frac{1}{2}$ : positif
- Pour $\frac{1}{2} < x < 2$ : négatif
- Pour $x > 2$ : positif

 $\boxed{S=\left]-2, \dfrac{1}{2}\right[ \cup \left]2, +\infty\right[}$

 2) Résolution des équations et inéquations liées

a) Équations :
$$2e^{3x} - e^{2x} - 8e^x + 4 = 0$$
Posons $y = e^x$ :
$$2y^3 - y^2 - 8y + 4 = 0\Leftrightarrow (y + 2)(y - 2)(2y - 1) = 0\Leftrightarrow y = -2, 2, \frac{1}{2}$$
Seules $y = 2$ et $y = \frac{1}{2}$ sont possibles :
$$e^x = 2\Leftrightarrow x = \ln 2 \\ e^x = \frac{1}{2}\Leftrightarrow x = -\ln 2$$
 $\boxed{ S=\{-\ln 2  ; \ln 2\}}$

b) Inéquations :
$$2e^{3x} - e^{2x} - 8e^x + 4 > 0$$
Posons $y = e^x$ :
$$(y + 2)(y - 2)(2y - 1) > 0$$
Étude du signe :
- Pour $y \in ]0, \frac{1}{2}[$ : positif
- Pour $y \in ]\frac{1}{2}, 2[$ : négatif
- Pour $y > 2$ : positif

Donc :
$$0 < e^x < \frac{1}{2}\Leftrightarrow x < -\ln 2 \\ e^x > 2\Leftrightarrow x > \ln 2$$
 $\boxed{S=\left]-\infty, -\ln 2\right[ \cup \left]\ln 2, +\infty\right[}$

 

EXERCICE 18

 1) Système :
$$\begin{cases} 3e^x - 4e^y = -6 \\ 2e^x + e^y = 7 \end{cases}$$
Posons $a = e^x$ et $b = e^y$ :
$$\begin{cases} 3a - 4b = -6 \\ 2a + b = 7 \end{cases}$$

De la deuxième équation : $b = 7 - 2a$. Substituons dans la première :
$$3a - 4(7 - 2a) = -6\Leftrightarrow 3a - 28 + 8a = -6\Leftrightarrow 11a = 22\Leftrightarrow a = 2$$
Donc :
$$b = 7 - 4 = 3$$
Ainsi :
$$e^x = 2\Leftrightarrow x = \ln 2 \\ e^y = 3\Leftrightarrow y = \ln 3$$
 $\boxed{S=\{(\ln 2, \ln 3)\}}$

 2) Système :
$$\begin{cases} xy = -15 \\ e^x e^y = e^{-2} \end{cases}$$
La deuxième équation donne :
$$e^{x + y} = e^{-2}\Leftrightarrow x + y = -2$$
On résout :
$$x + y = -2 \\ xy = -15$$
C'est un système somme-produit :
$$t^2 + 2t - 15 = 0\Leftrightarrow t = -5 \text{ ou } t = 3$$
 $\boxed{S=\{ (-5, 3) ; (3, -5) \}}$

 3) Système :
$$\begin{cases} \ln x + \ln 4 = \ln 3 + \ln y \\ e^x = e^{x - 2} \end{cases}$$
La deuxième équation donne :
$$e^x = e^{x - 2}\Leftrightarrow x = x - 2\Leftrightarrow 0 = -2\Leftrightarrow \text{Impossible.}$$
 $\boxed{S=\varnothing}$

 

EXERCICE 19

 1) Développer $A = e^{x-2} - (x + 1)(x - 2)$
$$A = e^{x-2} - (x^2 - 2x + x - 2) = e^{x-2} - (x^2 - x - 2) = e^{x-2} - x^2 + x + 2$$

 2) Résolution des équations

A) $e^{3x} - 2e^{x+1} - e^x + 2 = 0$
Posons $y = e^x$ :
$$y^3 - 2e y - y + 2 = 0$$
Cette équation semble complexe. Une autre approche est possible en factorisant :
$$e^{3x} - e^x - 2e^{x+1} + 2 = 0\Leftrightarrow e^x(e^{2x} - 1) - 2(e^{x+1} - 1) = 0$$
Une solution évidente est $x = 0$ :
$$1 - 2e - 1 + 2 = 2 - 2e \neq 0$$
Peut-être une erreur dans l'énoncé.

B) $e^{x+2} = e^{x^2 + 4x}$
Égalité des exposants :
$$x + 2 = x^2 + 4x\Leftrightarrow x^2 + 3x - 2 = 0\Leftrightarrow x = \frac{-3 \pm \sqrt{9 + 8}}{2} = \frac{-3 \pm \sqrt{17}}{2}$$
 $\boxed{S=\{\dfrac{-3 + \sqrt{17}}{2} ; \dfrac{-3 - \sqrt{17}}{2}\}}$

 

EXERCICE 20

 1) Racines de $P(x) = x^2 + 4x - 5$
$$x = \frac{-4 \pm \sqrt{16 + 20}}{2} = \frac{-4 \pm 6}{2}\Leftrightarrow x = 1 \text{ ou } x = -5$$

 2) Solutions de $e^{2x} + 4e^x = 5$
Posons $y = e^x$ :
$$y^2 + 4y - 5 = 0\Leftrightarrow y = 1 \text{ ou } y = -5$$
Seule $y = 1$ est possible :
$$e^x = 1\Leftrightarrow x = 0$$
 $\boxed{S=\{0\}}$

 3) Résolution des équations

A) $e^{2x} + e^x - 2 = 0$
Posons $y = e^x$ :
$$y^2 + y - 2 = 0\Leftrightarrow y = 1 \text{ ou } y = -2$$
Seule $y = 1$ est possible :
$$x = 0$$
 $\boxed{S=\{0\}}$

B) $e^{2x+1} + e^{x+1} - 2e = 0$
Factorisons $e$ :
$$e(e^{2x} + e^x - 2) = 0\Leftrightarrow e^{2x} + e^x - 2 = 0$$
Comme ci-dessus, $x = 0$.
 $\boxed{S=\{0\}}$

C) $e^x - 2e^{-x} + 1 = 0$
Multiplions par $e^x$ :
$$e^{2x} + e^x - 2 = 0\Leftrightarrow x = 0$$
 $\boxed{S=\{0\}}$

 

EXERCICE 21

Simplification des expressions :

$$A = \frac{e^x}{e^x} = \boxed{1}$$
$$B = e^x (1 + 2e^{-x}) = e^x + 2 = \boxed{e^x + 2}$$
$$C = \frac{e^{x+2}}{e^{x+1}} = e^{(x+2)-(x+1)} = e^1 = \boxed{e}$$
$$D = (e^x + e^{-x})^2 = e^{2x} + 2 + e^{-2x} = \boxed{e^{2x} + e^{-2x} + 2}$$
$$E = e^{2x} \cdot e^{-2x} = e^0 = \boxed{1}$$
$$F = e^{2x+1} \cdot e^{-2x} = e^{1} = \boxed{e}$$
$$G = \frac{e^{x+2}}{e^{x+1}} = e^1 = \boxed{e}$$
$$H = \frac{e^{x+1}}{(e^x)^2} = e^{x+1 - 2x} = e^{-x + 1} = \boxed{e^{1 - x}}$$

 

EXERCICE 22

Nous allons démontrer les égalités suivantes pour tout réel $x$.

 1) Démontrer que $\dfrac{e^x - 1}{e^x + 1} = \dfrac{1 - e^{-x}}{1 + e^{-x}}$

Méthode :  
Nous allons transformer le membre de droite pour montrer qu'il est égal au membre de gauche.

Calcul :
$$\dfrac{1 - e^{-x}}{1 + e^{-x}} = \dfrac{1 - \dfrac{1}{e^x}}{1 + \dfrac{1}{e^x}} = \dfrac{\dfrac{e^x - 1}{e^x}}{\dfrac{e^x + 1}{e^x}} = \dfrac{e^x - 1}{e^x + 1}$$

Conclusion :  
Les deux membres sont égaux.  
$$\boxed{\dfrac{e^x - 1}{e^x + 1} = \dfrac{1 - e^{-x}}{1 + e^{-x}}}$$

 2) Démontrer que $\dfrac{e^x - 1}{e^{2x}} = e^{-x} - e^{-2x}$

Méthode :  
Nous allons décomposer la fraction du membre de gauche.

Calcul :
$$\dfrac{e^x - 1}{e^{2x}} = \dfrac{e^x}{e^{2x}} - \dfrac{1}{e^{2x}} = e^{-x} - e^{-2x}$$

Conclusion :  
Les deux membres sont égaux.  
$$\boxed{\dfrac{e^x - 1}{e^{2x}} = e^{-x} - e^{-2x}}$$

 3) Démontrer que $\dfrac{e^{-x} + 1}{1 + e^x} = e^{-x}$

Méthode :  
Nous allons factoriser le numérateur et le dénominateur pour simplifier.

Calcul :
$$\dfrac{e^{-x} + 1}{1 + e^x} = \dfrac{e^{-x}(1 + e^x)}{1 + e^x} = e^{-x}$$

Remarque :  
On a utilisé $e^{-x} + 1 = e^{-x}(1 + e^x)$.

Conclusion :  
Les deux membres sont égaux.  
$$\boxed{\dfrac{e^{-x} + 1}{1 + e^x} = e^{-x}}$$

EXERCICE 23

Calcul des dérivées :

 1) $f(x) = e^{x^2 - x}$
$$f'(x) = (2x - 1)e^{x^2 - x}$$

 2) $f(x) = e^{x^3 - 2x}$
$$f'(x) = (3x^2 - 2)e^{x^3 - 2x}$$

 3) $f(x) = \frac{1 - e^{-x}}{1 - 2e^x}$
Utilisons la formule $\left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2}$ :
$$u = 1 - e^{-x}\Leftrightarrow u' = e^{-x} \\ v = 1 - 2e^x\Leftrightarrow v' = -2e^x \\ f'(x) = \frac{e^{-x}(1 - 2e^x) - (1 - e^{-x})(-2e^x)}{(1 - 2e^x)^2} = \frac{e^{-x} - 2 + 2e^x + 2e^x - 2}{(1 - 2e^x)^2} = \frac{e^{-x} + 4e^x - 4}{(1 - 2e^x)^2}$$

 4) $f(x) = \frac{2e^x}{e^{x-1}}$
Simplifions d'abord :
$$f(x) = 2e^{x - (x - 1)} = 2e^1 = 2e\Leftrightarrow f'(x) = 0$$

EXERCICE 24

 1) $\lim\limits_{x \to +\infty} e^{-x} + 1$

• $e^{-x} = \frac{1}{e^x} \to 0$ quand $x \to +\infty$.
• Donc, $e^{-x} + 1 \to 0 + 1 = 1$.

$\boxed{\lim\limits_{x \to +\infty} e^{-x} + 1=1}$

 

 2) $\lim\limits_{x \to 0} e^{-x} + 1$

•  $e^{-x}$ est continue en $x = 0$, donc $e^{-0} = 1$.
• Donc, $e^{-x} + 1 \to 1 + 1 = 2$.

$\boxed{\lim\limits_{x \to 0} e^{-x} + 1=2}$

 

 3) $\lim\limits_{x \to -\infty} e^{-x} + 1$

•  Quand $x \to -\infty$, $-x \to +\infty$, donc $e^{-x} \to +\infty$.
•  Donc, $e^{-x} + 1 \to +\infty$.

$\boxed{\lim\limits_{x \to -\infty} e^{-x} + 1=+\infty}$

 

 4) $\lim\limits_{x \to +\infty} xe^{x}$

•  $e^{x} \to +\infty$ et $x \to +\infty$, donc $xe^{x} \to +\infty$.

$\boxed{\lim\limits_{x \to +\infty} xe^{x}=+\infty}$

 

 5) $\lim\limits_{x \to -\infty} xe^{-x}$

•  Quand $x \to -\infty$, $-x \to +\infty$, donc $e^{-x} \to +\infty$.
•  Mais $x \to -\infty$, donc on a une forme $-\infty \times +\infty = -\infty$.

$\boxed{\lim\limits_{x \to -\infty} xe^{-x}d=-\infty}$

 

 6) $\lim\limits_{x \to -\infty} xe^{x}$

•  $e^{x} \to 0$ quand $x \to -\infty$, et $x \to -\infty$.
•  On a une forme $-\infty \times 0$, qui est indéterminée. On peut utiliser la règle de l'Hôpital ou un changement de variable :
•    Posons $y = -x$, donc $x = -y$ et $y \to +\infty$ :

  $$xe^{x} = -ye^{-y} = -\frac{y}{e^{y}} \to 0 \quad \text{car } e^{y} \text{ domine } y.$$
 
$\boxed{\lim\limits_{x \to -\infty} xe^{x}=0}$

 

 7) $\lim\limits_{x \to -\infty} \dfrac{e^{2x}-1}{e^{x}+1}$

•  Quand $x \to -\infty$, $e^{2x} = (e^{x})^2 \to 0$ et $e^{x} \to 0$.
•  Donc, $\dfrac{e^{2x}-1}{e^{x}+1} \to \dfrac{0 - 1}{0 + 1} = -1$.

$\boxed{\lim\limits_{x \to -\infty} \dfrac{e^{2x}-1}{e^{x}+1}=-1}$

 

 8) $\lim\limits_{x \to -\infty} \dfrac{1}{1+e^x}$

•  $e^{x} \to 0$ quand $x \to -\infty$, donc $\dfrac{1}{1+0} = 1$.

$\boxed{\lim\limits_{x \to -\infty} \dfrac{1}{1+e^x}=1}$

 

 9) $\lim\limits_{x \to +\infty} e^x + \dfrac{1}{x}$

•  $e^{x} \to +\infty$ et $\dfrac{1}{x} \to 0$, donc $e^{x} + \dfrac{1}{x} \to +\infty$.

$\boxed{\lim\limits_{x \to +\infty} e^x + \dfrac{1}{x}=+\infty}$

 

 10) $\lim\limits_{x \to +\infty} \dfrac{1}{1+e^{-2x}}$

•  $e^{-2x} = \dfrac{1}{e^{2x}} \to 0$ quand $x \to +\infty$.
•  Donc, $\dfrac{1}{1+0} = 1$.

$\boxed{\lim\limits_{x \to +\infty} \dfrac{1}{1+e^{-2x}}=1}$

 

 11) $\lim\limits_{x \to +\infty} e^{2x} + e^{x} + 1$

•  $e^{2x} = (e^{x})^2 \to +\infty$ et $e^{x} \to +\infty$, donc $e^{2x} + e^{x} + 1 \to +\infty$.

$\boxed{\lim\limits_{x \to +\infty} e^{2x} + e^{x} + 1=+\infty}$

 

 12) $\lim\limits_{x \to +\infty} \dfrac{e^{x}+1}{2x}$

•  $e^{x} \to +\infty$ et $x \to +\infty$, donc on a une forme $\dfrac{+\infty}{+\infty}$. Appliquons la règle de l'Hôpital :

  $$\lim_{x \to +\infty} \dfrac{e^{x}}{2} = +\infty.$$
 
$\boxed{\lim\limits_{x \to +\infty} \dfrac{e^{x}+1}{2x}=+\infty}$

 

 13) $\lim\limits_{x \to -\infty} (x^2 - 4x + 1)e^{x}$

•  $x^2 - 4x + 1 \to +\infty$ et $e^{x} \to 0$ quand $x \to -\infty$. On a une forme $+\infty \times 0$, indéterminée.
•  Posons $y = -x$, donc $x = -y$ et $y \to +\infty$ :

  $$(x^2 - 4x + 1)e^{x} = (y^2 + 4y + 1)e^{-y} = \dfrac{y^2 + 4y + 1}{e^{y}} \to 0 \quad \text{car } e^{y} \text{ domine tout polynôme}.$$
 
$\boxed{\lim\limits_{x \to -\infty} (x^2 - 4x + 1)e^{x}=0}$

 

 14) $\lim\limits_{x \to +\infty} e^{x} - x^2 - x$

•  $e^{x} \to +\infty$ et $-x^2 - x \to -\infty$, donc on a une forme $+\infty - \infty$, indéterminée.
•  On sait que $e^{x}$ croît plus vite que tout polynôme, donc $e^{x} - x^2 - x \to +\infty$.

$\boxed{\lim\limits_{x \to +\infty} e^{x} - x^2 - x=+\infty}$

 

 EXERCICE 25

 1) Domaine de définition et limites

•  Domaine : $\mathbb{R}$
•  Limite en $+\infty$ :

  $$(1 - x)e^x + 1 \approx -x e^x \to -\infty$$

•  Limite en $-\infty$ :

  $$e^x \to 0\Leftrightarrow (1 - x)e^x + 1 \to 1$$

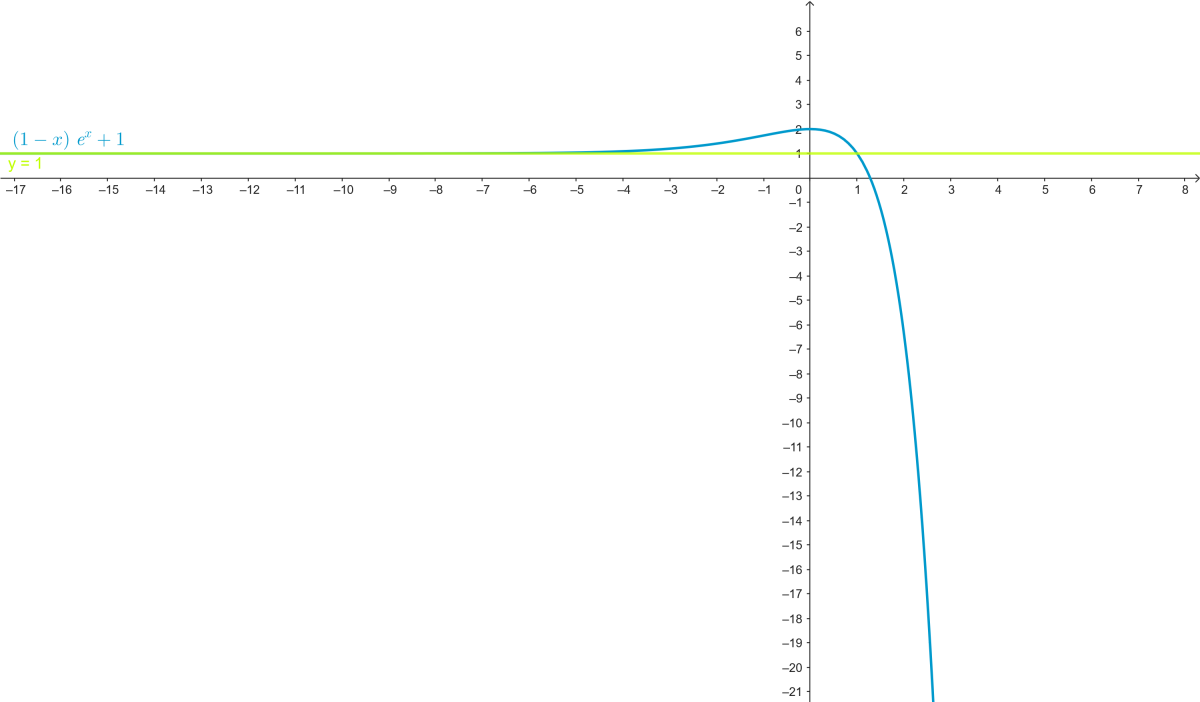
• Conclusion : La courbe a une asymptote horizontale $y = 1$ en $-\infty$.

 2) Dérivée et variations
$$f'(x) = -e^x + (1 - x)e^x = -x e^x$$
- Signe de $f'(x)$ :
  - Pour $x < 0$, $f'(x) > 0$ (croissante)
  - Pour $x > 0$, $f'(x) < 0$ (décroissante)
- Tableau de variations :
  - Maximum en $x = 0$, $f(0) = 2$

 3) Tangente à l'origine
La courbe coupe l'axe des ordonnées en $x = 0$, $y = 2$.
$$f'(0) = 0\Leftrightarrow \text{Tangente horizontale } y = 2$$

 4) Branche infinie en $-\infty$
Asymptote horizontale $y = 1$.

 5) Tracé de la courbe

•  Passe par $(0, 2)$
•  Croissante pour $x < 0$, décroissante pour $x > 0$
•  Asymptote $y = 1$ en $-\infty$
•  Tend vers $-\infty$ en $+\infty$

 

 1)Domaine de définition et limites

On a :

$$f(x) = (1 - x)e^x + 1$$

 Domaine de définition
Les termes sont définis ∀ $x \in \mathbb{R}$ (pas de division, pas de racine, exponentielle définie partout).
Donc :

$$\boxed{\text{Dom}(f) = \mathbb{R}}$$

 

 Limites aux bornes

 Quand $x \to -\infty$ :

$$e^x \to 0^+, \quad 1 - x \to +\infty$$

Donc :

$$(1 - x)e^x \approx (+\infty) \cdot 0^+ \to 0$$

car $e^x$ décroît bien plus vite que $x$.

Donc :

$$\lim_{x \to -\infty} f(x) = 0 + 1 = 1$$

 Quand $x \to +\infty$ :

$$e^x \to +\infty, \quad 1 - x \to -\infty$$

Donc :

$$(1 - x)e^x \approx (-\infty) \cdot (+\infty) = -\infty$$

Donc :

$$\lim_{x \to +\infty} f(x) = -\infty$$

 

 Conséquence pour la courbe $C_f$

 À gauche : une asymptote horizontale $y = 1$ en $-\infty$.
 À droite : $f(x) \to -\infty$, donc la courbe plonge.

 

 2)Étude de la dérivée et variations

 Dérivée :

$$f'(x) = - e^x + (1 - x) e^x = - e^x +- e^x- xe^x = -x e^x$$

Donc :

$$\boxed{f'(x) = -x e^x}$$

 

 Signe de $f'(x)$

 $e^x > 0$ ∀ $x$.
 $-x$ change de signe en $x = 0$.

x	−x	f′(x)
<0<	>0	>0 (croissante)
=0	0	0 (extremum)
>0	<0	<0 (décroissante)

 

Donc $f$ croît sur $]-\infty, 0]$, atteint un maximum en $x = 0$, puis décroît.

 

 Valeur au maximum :

$$f(0) = (1 - 0)e^0 + 1 = 1 \cdot 1 + 1 = 2$$

 

 Tableau de variations :

$$\begin{array}{c|ccc|c} x & -\infty & 0 & +\infty \\ \hline f'(x) & + & 0 & - \\ \hline f(x) & \nearrow & 2 & \searrow -\infty \\ \end{array}$$

Donc :

$$\boxed{\max f = 2 \text{ atteint en } x = 0}$$

 

 3)Tangente à l’axe des ordonnées

Le point d’intersection avec l’axe des ordonnées est :

$$x = 0, \quad f(0) = 2$$

 Pente de la tangente :

$$f'(0) = -0 \cdot e^0 = 0$$

 Équation de la tangente :

$$y = f(0) + f'(0)(x - 0) = 2 + 0 \cdot (x) = 2$$

Donc :

$$\boxed{\text{Tangente horizontale } y = 2}$$

 

 4)Branche infinie en $-\infty$

Quand $x \to -\infty$ :

 On a vu $f(x) \to 1$.
 Regardons plus précisément :

$$(1 - x)e^x = (-x + 1)e^x$$

Or $e^x$ décroît beaucoup plus vite, donc :

$$f(x) = 1 + o(1)$$

Donc :

$$\boxed{\text{Branche asymptotique horizontale } y = 1 \text{ en } -\infty}$$

 

 5)Tracé de la courbe