Baccalauréat S Antilles - Guyane 9 septembre 2020

Dans cet exercice, sauf mention contraire, les résultats seront arrondis au millième.

Les parties $A$, $B$ et $C$ peuvent être traitées de façon indépendante.

Louise se rend au travail avec sa voiture.

Sa collègue Zoé ne possède pas de voiture.
 
Chaque matin, Louise propose donc à Zoé de l'emmener.

Quelle que soit la réponse de Zoé, Louise lui propose de la ramener le soir.

On se place un jour donné.

On dispose des informations suivantes :

$\bullet\ $la probabilité que Louise emmène Zoé le matin est $0.55$ ;

$\bullet\ $si Louise a emmené Zoé le matin, la probabilité qu'elle la ramène le soir est $0.7$ ;

$\bullet\ $si Louise n'a pas emmené Zoé le matin,la probabilité qu'elle la ramène le soir est $0.24$

On note $M$ et $S$ les événements suivants:

$\bullet\ M$ :« Louise emmène Zoé le matin » ;

$\bullet\ S$ :« Louise ramène Zoé le soir ».

1. Construire un arbre pondéré traduisant la situation.

2. Calculer $P(M\cap S)$

Traduire ce résultat par une phrase.

3. Démontrer que la probabilité de l'événement $S$ est égale à $0.493$

4. On sait que Louise a ramené Zoé le soir.

Quelle est la probabilité que Louise l'ait emmenée le matin?
 

Le temps de trajet de Louise, en minute, entre son domicile et son travail, peut être modélisé par une variable aléatoire $X$ qui suit la loi normale d'espérance $28$ et d'écart-type $5.$

1. Calculer $P\left(X\geq 25\right)$

2. Calculer la probabilité que le temps de trajet soit compris entre $18$ et $38$ minutes.

3. Déterminer la durée $d$ du trajet, arrondie à la minute, telle que $P\left(X\geq d\right)$

4. Louise a maintenant trouvé un itinéraire plus rapide.

 Désormais, le temps de trajet, en minute, peut être modélisé par une variable aléatoire $Y$ qui suit la loi normale d'espérance $26$ et d'écart-type $\delta$

On sait que $P\left(Y\geq 30\right)=0.1$

Déterminer l'arrondi au centième de $\delta$

L'entreprise de Louise indique sur son site internet que $35\%$ de ses salariés pratiquent le covoiturage.

Un sondage effectué au sein de l'entreprise montre que sur $254$ salariés choisis au hasard, $82$

pratiquent le covoiturage.

Ce sondage remet t-il en cause l'information publiée par l'entreprise sur son site internet?

 

La partie $C$ est indépendante des parties $A$ et $B$

La fonction $g$ est définie sur $[0\ ;\ +\infty[$ par $$g(x)=1-\mathrm{e}^{-x}$$

On admet que la fonction $g$ est dérivable sur [0 ; +∞[. $[0\ ;\ +\infty[$

1. Déterminer la limite de la fonction $g$ en $+\infty$

2. Étudier les variations de la fonction $g$ sur $[0\ ;\ +\infty[$ et dresser son tableau de variations.

Dans cette partie, $k$ désigne un réel strictement positif.

On considère la fonction $f$ définie sur $R$ par $$f(x)=(x-1)\mathrm{e}^{-kx}+1$$

On admet que la fonction $f$ est dérivable sur $\mathbb{R}$ et on note $f'$ sa fonction dérivée.

Dans le plan muni d'un repère orthonormé $(O\ ;\ I\;,J)$,on note $\mathbb{C}_{f}$ la courbe représentative de la fonction $f.$

Cette courbe est représentée ci-dessous pour une certaine valeur de $k.$

La tangente $T$ à la courbe $\mathbb{C}_{f}$

au point $A$ d'abscisse $1$ coupe l'axe des ordonnées en un point noté $B.$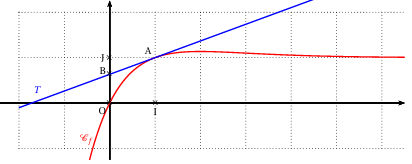

1.a. Démontrer que pour tout réel $x$,

$$f'(x)=\mathrm{e}^{-kx}(-kx+k+1)$$

b. Démontrer que l'ordonnée du point $B$ est égale à  $g(k)$ où $g$ est la fonction définie dans la

 2. En utilisant la partie $A$, démontrer que le point $B$ appartient au segment $[0J]$
 
Dans cette partie, on considère la fonction $h$ définie sur $R$ par
$$h(x)=(x-1)\mathrm{e}^{-2x}+1$$

On admet que la fonction $h$ est dérivable sur $R$

On se place dans un repère orthonormé $(O\ ; I\;, j)$

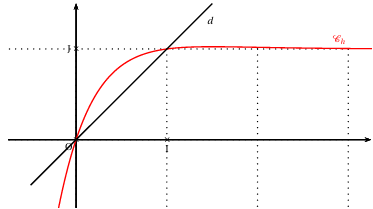
On note $\mathbb{C}_{h}$ la courbe représentative de la fonction $h$ et $d$ la droite d'équation $y=x$

La courbe $\mathbb{C}_{h}$ et la droite $d$ sont représentées sur l'annexe $1$ à rendre avec la copie.

On admet que la courbe $\mathbb{C}_{h}$ est au-dessus de la droite $d$ sur l'intervalle $[0\ ;\ 1[$

Soit $D$ le domaine du plan délimité par la courbe , la droite d et les droites verticales d'équations $x=0$ et $x=1$
 
Soit $\mathbb{A}$ l'aire de $\mathbb{D}$ exprimée en unité d'aire.
 
1.a. Sur l'annexe $1$ à rendre avec la copie, hachure le domaine $\mathbb{D}$ et justifier que $$\mathbb{A}=\int_{0}^{1}[h(x)-x]dx$$

2.a. Démontrer que, pour tout réel $x$, $$h(x)-x=(1-x)\left(x-\mathrm{e}^{-2x}\right)$$

b. On admet que, pour tout réel $x$, $\mathrm{e}^{-2x}\geq 1-2x$

Démontrer que, pour tout réel $x$ de l'intervalle $[0\ ;\ 1]$ $$h(x)-x\leq 2x-2x^{2}$$

c. En déduire que $\mathbb{A}\geq \dfrac{1}{3}$

3. Soit $H$ la fonction définie sur $[0\ ;\ 1]$ par $$H(x)=\dfrac{1}{4}(1-2x)\mathrm{e}^{-2x}+x$$

On admet que la fonction $H$ est une primitive de la fonction $h$ sur $[0\ ;\ 1]$

Déterminer la valeur exacte de $A$

Dans le cube $ABCOEFGH$ ci-dessous et reproduit en ANNEXE $2$ à rendre avec la copie,on a placé les points $M$ et $N$ milieux respectifs des segments $[AB]$ et $[BC]$

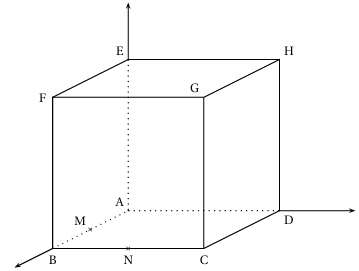
On se place dans le repère $\left(A\ ;\ \overrightarrow{AB}\;,\overrightarrow{AD}\;,\overrightarrow{AE}\right)$

1. Donner sans justifier les coordonnées des points $H$, Met $N$

2. On admet que les droites $(CD)$ et $(MN)$ sont sécantes et on note $K$ leur point d'intersection.

a. Donner une représentation paramétrique de la droite $(MN)$

On admet qu'une représentation paramétrique de la droite $(CD)$ est
$$\left\lbrace\begin{array}{rcl} x&=&t\\ y&=&1\quad t\in\mathbb{R}\\ z&=&0 \end{array}\right.$$

b. Déterminer les coordonnées du point $K$

3. On admet que les points $H$, $M$, $N$ définissent un plan et que la droite $(CG)$ et le plan $(HMN)$ sont sécants.

On note $L$ leur point d'intersection.

a. Vérifier que le vecteur $\overrightarrow{n}\begin{pmatrix} 2\\ -2\\ 3 \end{pmatrix}$ est un vecteur normal au plan $(HMN)$

b. Déterminer une équation cartésienne du plan $(HMN)$

c. En déduire les coordonnées du point
 
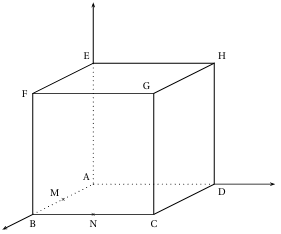
4. Sur l'annexe $2$ à rendre avec la copie, construire les points $K$ et $L$ puis la section du cube $ABCDEFGH$ par le plan $(HMN)$
 

Candidats n'ayant pas suivi l'enseignement de spécialité

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse.

 Il est attribué un point par réponse exacte correctement justifiée.
 
Une réponse non justifiée n'est pas prise en compte.
 
Une absence de réponse n'est pas pénalisée.

1. Soit $\left(u_{n}\right)$ la suite définie par $u_{0}=4$ pour tout entier naturel $n\;,u_{n+1}=-\dfrac{2}{3}u_{n}+1$ et soit $\left(v_{n}\right)$ la suite définie par

pour tout entier naturel $n\;,v_{n}=u_{n}-\dfrac{2}{3}$

Affirmation $1$ : La suite $\left(v_{n}\right)$ est une suite géométrique.

2. Soit $\left(w_{n}\right)$ la suite définie par, pour tout entier naturel $n$ non nul, $$w_{n}=\dfrac{3+\cos(n)}{n^{2}}$$

Affirmation $2$ : La suite $\left(w_{n}\right)$ converge vers $0$

3. On considère l'algorithme suivant :

$\boxed{U\longleftarrow 5\\ N\longleftarrow 0\\ \text{Tant que }U\leq 5000\\ U\longleftarrow 3\times U-8\\
N\longleftarrow N+1\\ \text{Fin Tant que}}$

Affirmation $3$ :

À la fin de l'exécution, la variable $U$ contient la valeur $5000$

4. On note $C$ l'ensemble des nombres complexes.

On considère l'équation $(E)$ d'inconnue $z$ dans $C$ $$(z-i)\left(z^{2}+z\sqrt{3}+1\right)=0$$

Affirmation $4$ : Toutes les solutions de l'équation $(E)$ sont de module $1$

5. On considère les nombres complexes $z_{n}$ définis par $z_{0}=2$ et pour tout entier naturel $n$ $n_{n+1}=2\mathrm{e}^{i\dfrac{\pi}{2}}z_{n}$$

On munit le plan complexe d'un repère orthonormé direct $\left(0\ ;\ \vec{u}\;,\vec{v}\right)$

Pour tout entier naturel $n$, on note $M_{n}$ le point d'affixe $z_{n}$

Affirmation $5$ : Pour tout entier naturel $n$, le point $0$ est le milieu du segment $\left[M_{n}M_{n+2}\right)$

Candidats ayant suivi l'enseignement de spécialité

On considère l'équation $(E)$  $$x^{2}-5y^{2}=1$$ où $x$ et $y$ sont des entiers naturels.

On suppose que $(x\ ;\ y)$ est un couple solution de l'équation $(E)$

1. $x$ et $y$ peuvent-ils avoir la même parité?

Justifier.

2. Démontrer que $x$ et $y$ sont premiers entre eux.
 
3. Soit $k$ un entier naturel.

Recopier et compléter le tableau suivant

$\begin{array}{|c|c|c|c|c|c|} \hline \text{Reste de la division eu-}&0&1&2&3&4\\ \text{clidienne de }k\text{ par }5&&&&&\\ \hline \text{reste de la division eu- }&&&&&\\ \text{clidienne de }k^{2}\text{ par }5\\&&&&&\\ \hline \end{array}$

En déduire que $x\equiv 1[5]$ ou $x\equiv 4[5]$

Soit $A$ la matrice $\begin{pmatrix} 9\quad 20\\ 4\quad 9 \end{pmatrix}$

On considère les suites $\left(x_{n}\right)$ et $\left(y_{n}\right)$ définies par $x_{0}=1$ et $y_{0}=0$, et pour tout entier naturel$n$, $\begin{pmatrix} x_{n+1}\\ y_{n+1} \end{pmatrix}=A\begin{pmatrix} x_{n}\\ y_{n} \end{pmatrix}$

1. Pour tout entier naturel $n$, exprimer $x_{n+1}$ et $y_{n+1}$ en fonction de $x_{n}$ et $y_{n}$

2. Démontrer par récurrence que, pour tout entier naturel $n$, $x_{n}$, $y_{n}$ est solution de l'équation $(E)$

3.a. Déterminer $A_{2}$,puis en déduire $x_{2}$ et $y_{2}$

b. Soit $P$ un entier naturel.

Démontrer que si $y_{p}$ est un multiple de $9$ alors $y_{p+2}$ est aussi un multiple de $9$

c. En déduire que $y_{2020}$ est un multiple de $9.$

A Rendre avec la copie

Annexe $1$ (exercice $2$, partie $C$)

Annexe $2$ (exercice $3$)