Solutions Serie d'exercices : Système d'équation et inéquation du 1er degré à deux inconnues - 2nd L

Exercice 1 : Méthode de substitution

Système $S_1$
$$\{\begin{array}{rcl}x-y+7& =& 0\\ 3x+y-7& =& 0\end{array}$$
1. Isoler $y$ dans la première équation :
   $$x-y+7=0⟹y=x+7$$

2. Substituer $y$ dans la deuxième équation :
   $$3x+(x+7)-7=0⟹4x=0⟹x=0$$

3. Trouver $y$ :
   $$y=0+7=7$$

Solution : $(x,y)=(0,7)$

 Système $S_2$
$$\{\begin{array}{rcl}x-y-2& =& 0\\ 2x+y+5& =& 0\end{array}$$

1. Isoler $y$ dans la première équation :
   $$x-y-2=0⟹y=x-2$$

2. Substituer $y$ dans la deuxième équation :
   $$2x+(x-2)+5=0⟹3x+3=0⟹x=-1$$

3. Trouver $y$ :
   $$y=-1-2=-3$$

Solution : $(x,y)=(-1,-3)$

 Système $S_3$
$$\{\begin{array}{rcl}2x+5y-16& =& 0\\ 3x+3y-15& =& 0\end{array}$$

1. Simplifier la deuxième équation :
   $$3x+3y-15=0⟹x+y=5⟹y=5-x$$

2. Substituer $y$ dans la première équation :
   $$2x+5(5-x)-16=0⟹2x+25-5x-16=0⟹-3x+9=0⟹x=3$$

3. Trouver $y$ :
   $$y=5-3=2$$

Solution : $(x,y)=(3,2)$

 Système $S_4$
$$\{\begin{array}{rcl}-{\displaystyle \frac{1}{3}}x+y-1& =& 0\\ 2x-{\displaystyle \frac{1}{4}}y+7& =& 0\end{array}$$

1. Isoler $y$ dans la première équation :
   $$-{\displaystyle \frac{1}{3}}x+y-1=0⟹y={\displaystyle \frac{1}{3}}x+1$$

2. Substituer $y$ dans la deuxième équation :
   $$2x-{\displaystyle \frac{1}{4}}({\displaystyle \frac{1}{3}}x+1)+7=0⟹2x-{\displaystyle \frac{1}{12}}x-{\displaystyle \frac{1}{4}}+7=0$$
   $${\displaystyle \frac{24}{12}}x-{\displaystyle \frac{1}{12}}x={\displaystyle \frac{1}{4}}-7⟹{\displaystyle \frac{23}{12}}x=-{\displaystyle \frac{27}{4}}⟹x=-{\displaystyle \frac{27}{4}}\times {\displaystyle \frac{12}{23}}=-{\displaystyle \frac{81}{23}}$$

3. Trouver $y$ :
   $$y={\displaystyle \frac{1}{3}}\times (-{\displaystyle \frac{81}{23}})+1=-{\displaystyle \frac{27}{23}}+{\displaystyle \frac{23}{23}}=-{\displaystyle \frac{4}{23}}$$

Solution : $(x,y)=(-{\displaystyle \frac{81}{23}},-{\displaystyle \frac{4}{23}})$

Exercice 2 : Méthode d'addition

 Partie a.
$$\{\begin{array}{rcl}x+3y& =& 1\\ 2x+y& =& 4\end{array}$$

1. Multiplier la première équation par 2 :
   $$2x+6y=2$$

2. Soustraire la deuxième équation :
   $$(2x+6y)-(2x+y)=2-4⟹5y=-2⟹y=-{\displaystyle \frac{2}{5}}$$

3. Trouver $x$ :
   $$x+3(-{\displaystyle \frac{2}{5}})=1⟹x=1+{\displaystyle \frac{6}{5}}={\displaystyle \frac{11}{5}}$$

Solution : $(x,y)=({\displaystyle \frac{11}{5}},-{\displaystyle \frac{2}{5}})$

 Partie b.
$$\{\begin{array}{rcl}2x+3y-1& =& 0\\ -3x+2y+5& =& 0\end{array}$$

1. Réécrire le système :
   $$\{\begin{array}{rcl}2x+3y& =& 1\\ -3x+2y& =& -5\end{array}$$

2. Multiplier la première équation par 3 et la deuxième par 2 :
   $$\begin{gathered} 6x+9y=3 \\ -6x+4y=-10 \end{gathered}$$

3. Additionner les deux équations :
   $$13y=-7⟹y=-{\displaystyle \frac{7}{13}}$$

4. Trouver $x$ :
   $$2x+3(-{\displaystyle \frac{7}{13}})=1⟹2x=1+{\displaystyle \frac{21}{13}}={\displaystyle \frac{34}{13}}⟹x={\displaystyle \frac{17}{13}}$$

Solution : $(x,y)=({\displaystyle \frac{17}{13}},-{\displaystyle \frac{7}{13}})$

 Partie c.
$$\{\begin{array}{rcl}3x+10y& =& 58\\ 10x+3y& =& 72\end{array}$$

1. Multiplier la première équation par 10 et la deuxième par 3 :
   $$\begin{gathered} 30x+100y=580 \\ 30x+9y=216 \end{gathered}$$

2. Soustraire la deuxième équation de la première :
   $$91y=364⟹y=4$$

3. Trouver $x$ :
   $$3x+10(4)=58⟹3x=18⟹x=6$$

Solution : $(x,y)=(6,4)$

 Partie d.
$$\{\begin{array}{rcl}{\displaystyle \frac{1}{3}}x-{\displaystyle \frac{1}{2}}y& =& 1\\ -x+{\displaystyle \frac{2}{3}}y& =& {\displaystyle \frac{2}{3}}\end{array}$$

1. Éliminer les fractions en multipliant par 6 et 3 respectivement :
   $$\begin{gathered} 2x-3y=6 \\ -3x+2y=2 \end{gathered}$$

2. Multiplier la première équation par 3 et la deuxième par 2 :
   $$\begin{gathered} 6x-9y=18 \\ -6x+4y=4 \end{gathered}$$

3. Additionner les deux équations :
   $$-5y=22⟹y=-{\displaystyle \frac{22}{5}}$$

4. Trouver $x$ :
   $$2x-3(-{\displaystyle \frac{22}{5}})=6⟹2x=6-{\displaystyle \frac{66}{5}}=-{\displaystyle \frac{36}{5}}⟹x=-{\displaystyle \frac{18}{5}}$$

Solution : $(x,y)=(-{\displaystyle \frac{18}{5}},-{\displaystyle \frac{22}{5}})$

Exercice 3 : Méthode graphique

 Système $S_1$
$$\{\begin{array}{rcl}x-y+3& =& 0\\ 2x-y+2& =& 0\end{array}$$

1. Trouver les points d :
  - L'équation $x-y+3=0$  
      Pour $x=0$, $y=3$ et $y=2$, $y=0$, $x=-3$ ).
      La droite passe par les points $A(0,3)$ et $B(-3,0)$
   - L'équation $2x-y+2=0$
      Pour $x=0$, $y=2$ et$y=0$, $x=-1$.
      La droite passe par les points $C(0,2)$ et $D(-1,0)$
3. Représentation graphique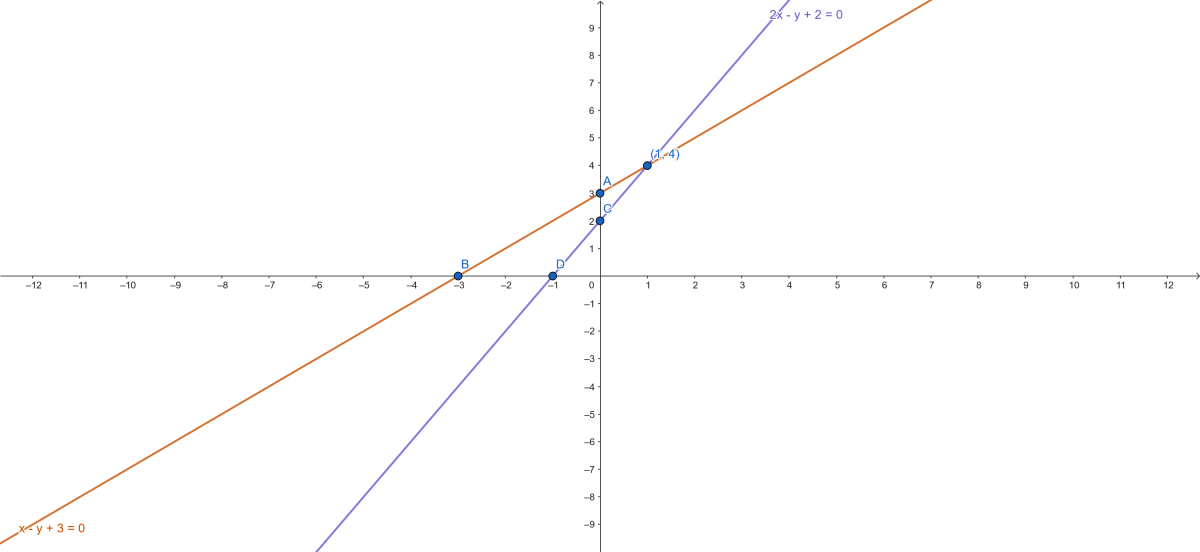

2. Solution graphique : Les droites se coupent en $(1,4)$.

Solution : $(x,y)=(1,4)$

 Système $S_2$
$$\{\begin{array}{rcl}2x-y-4& =& 0\\ 2x-y+2& =& 0\end{array}$$
-Représentation graphique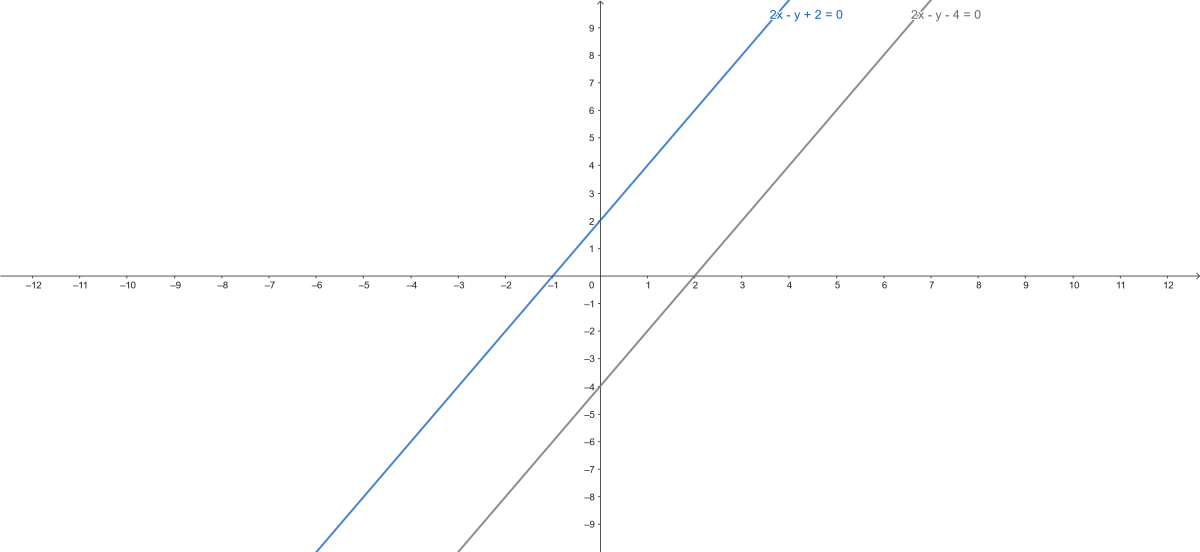

- Analyse : Les deux équations représentent des droites parallèles (même coefficient directeur).
 
Solution : Aucune solution (système incompatible).

 Système $S_3$
$$\{\begin{array}{rcl}x-y+3& =& 0\\ 2x-2y+6& =& 0\end{array}$$

- Analyse : La deuxième équation est un multiple de la première.
 
Solution : Infinité de solutions (droites confondues).

 Système $S_4$
$$\{\begin{array}{rcl}x-y-1& =& 0\\ 2x-y+2& =& 0\\ -x+3y+9& =& 0\end{array}$$
1. Résolution graphique

- L'équation $x-y-1=0$  
      Pour $x=0$, $y=-1$ et  $y=0$, $x=1$ ).
      La droite passent par les points $A(0,-1)$ et $B(1,0)$
- L'équation $2x-y+2=0$  
      Pour $x=0$, $y=2$ et  $y=0$, $x=-1$ ).
      La droite passent par les points $C(0,2)$ et $D(-1,0)$
- L'équation $-x+3y+9=0$  
      Pour $x=0$, $y=-3$ et  $y=0$, $x=9$ ).
      La droite passent par les points $E(0,-3)$ et $F(9,0)$

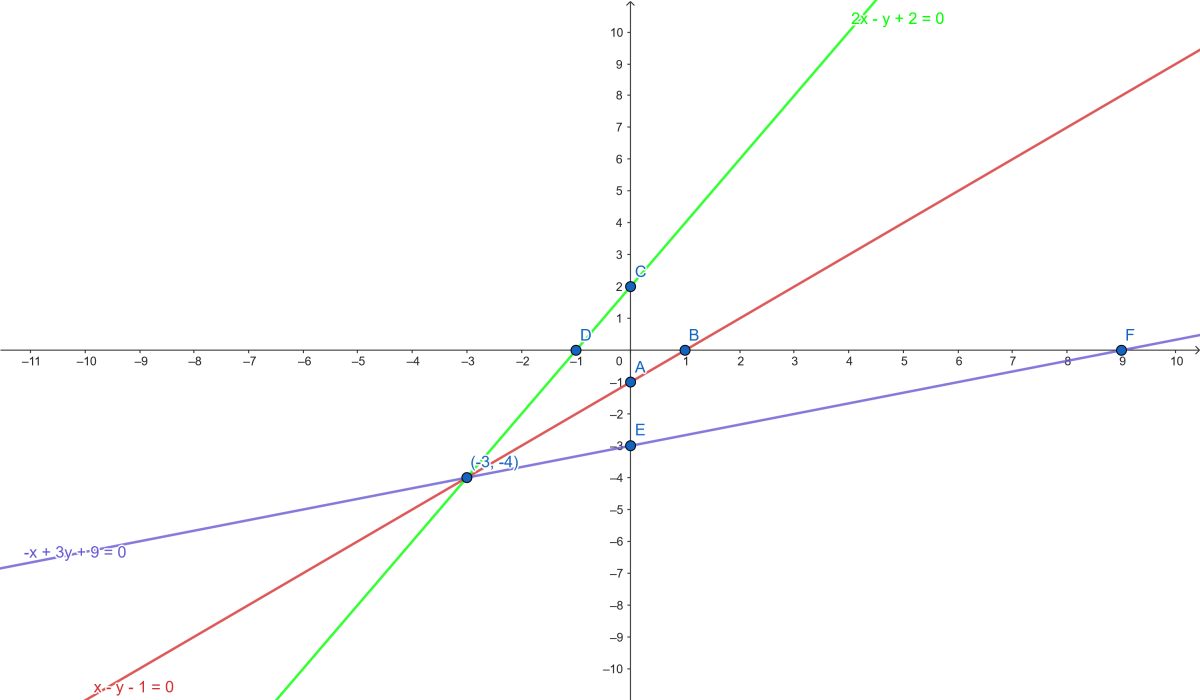
Les 3 droites se croisent au point $(-3,-4)$ qui est la solution du sytème

2. Résoudre les deux premières équations :
   $$\{\begin{array}{rcl}x-y& =& 1\\ 2x-y& =& -2\end{array}⟹x=-3,y=-4$$

2. Vérifier dans la troisième équation :
   $$-(-3)+3(-4)+9=3-12+9=0\text{(vérifié)}$$

Solution : $(x,y)=(-3,-4)$

Exercice 4 : Problème avec systèmes d'équations

Système à résoudre :
$$\{\begin{array}{rcl}x+2y& =& 625\\ 6x+13y& =& 3975\end{array}$$

Méthode : Nous allons utiliser la méthode de substitution ou de combinaison linéaire. Ici, la méthode de combinaison semble adaptée.

Étape 1 : Multiplions la première équation par 6 pour aligner les coefficients de $x$ avec la deuxième équation.
$$\begin{gathered} 6\times (x+2y)=6\times 625 \\ 6x+12y=3750 \end{gathered}$$

Étape 2 : Soustraisons cette nouvelle équation de la deuxième équation du système.
$$\begin{gathered} (6x+13y)-(6x+12y)=3975-3750 \\ 6x+13y-6x-12y=225 \\ y=225 \end{gathered}$$

Étape 3 : Substituons $y=225$ dans la première équation pour trouver $x$.
$$\begin{gathered} x+2\times 225=625 \\ x+450=625 \\ x=625-450 \\ x=175 \end{gathered}$$

Solution :
$$(x,y)=(175,225)$$

Vérification :
- Première équation : $175+2\times 225=175+450=625$ ✔️
- Deuxième équation : $6\times 175+13\times 225=1050+2925=3975$ ✔️

 Problème 2 : Application à la situation de Tante Adja

Contexte :
- Avant dévaluation :
  - Prix des pommes de terre : $p$ F/kg
  - Prix des oignons : $o$ F/kg
  - Coût total : $10p+20o=6250$

- Après dévaluation :
  - Prix des pommes de terre : $1.2p$ F/kg
  - Prix des oignons : $1.3o$ F/kg
  - Coût total : $10\times 1.2p+20\times 1.3o=7950$

Système d'équations :
$$\{\begin{array}{rcl}10p+20o& =& 6250\\ 12p+26o& =& 7950\end{array}$$

Simplification :
Divisons la première équation par 10 et la deuxième par 2 pour simplifier :
$$\{\begin{array}{rcl}p+2o& =& 625\\ 6p+13o& =& 3975\end{array}$$

Observation : Ce système est identique à celui du problème 1, avec $p=x$ et $o=y$.

Solution :
$$(p,o)=(175,225)$$

Interprétation :
- Avant dévaluation :
  - Prix d'un kg de pommes de terre : $175$ F CFA
  - Prix d'un kg d'oignons : $225$ F CFA

- Après dévaluation :
  - Prix d'un kg de pommes de terre : $1.2\times 175=210$ F CFA
  - Prix d'un kg d'oignons : $1.3\times 225=292.5$ F CFA

Vérification des coûts :
- Avant dévaluation : $10\times 175+20\times 225=1750+4500=6250$ F CFA ✔️
- Après dévaluation : $10\times 210+20\times 292.5=2100+5850=7950$ F CFA ✔️

 Conclusion

1. La solution du système d'équations est $(x,y)=(175,225)$.
2. Avant la dévaluation :
   - Le prix d'un kilogramme de pommes de terre était de 175 F CFA.
   - Le prix d'un kilogramme d'oignons était de 225 F CFA.

Ces valeurs satisfont toutes les conditions données dans le problème.

Exercice 6 : Problème de mélange

Contraintes :
$$\{\begin{array}{rcl}x+y& \ge & 10\\ 600x+400y& \le & 6000\\ x,y& \ge & 0\end{array}$$

1. Simplifier la deuxième inéquation :
   $$3x+2y\le 30$$

2. Représentation graphique :
   - Zone réalisable délimitée par $x+y\ge 10$, $3x+2y\le 30$, et $x,y\ge 0$.

Solution : Tous les couples $(x,y)$ dans la zone réalisable.