Corrigé du baccalauréat $S$ Métropole-la Réunion - 11 septembre 2020

On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x)=\dfrac{2\mathrm{e}^{x}}{\mathrm{e}^{x}+1}$

On donne ci-dessous la courbe représentative $\mathbb{C}$ de la fonction $f$ dans un repère orthonormé

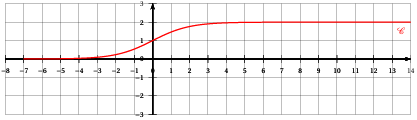
1. On sait que $\lim\limits_{x\longrightarrow\,-\infty}\mathrm{e}^{x}=0$, donc $\lim\limits_{x\longrightarrow\,-\infty}f(x)=\dfrac{0}{1}=0$

Ceci montre que la droite d'équation $y=2$ est asymptote horizontale à la courbe $\mathbb{C}$ en $\infty$

3. La fonction $f$ est dérivable sur $\mathbb{R}$ comme quotient de fonctions dérivables sur $\mathbb{R}$

$\begin{array}{rcl} f'(x)&=&\dfrac{2\mathrm{e}^{x}\left(\mathrm{e}^{x}+1\right)-\mathrm{e}^{x}+2\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}}\\&=&\dfrac{2\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}}\\&=&\dfrac{2\mathrm{e}^{x}}{\mathrm{e}^{x}+1}\times \dfrac{1}{\mathrm{e}^{x}+1}\\&=&\dfrac{f(x)}{\mathrm{e}^{x}+1} \end{array}$

 Pour tout $x$, $\mathrm{e}^{x}>0$ donc, comme $f(x)$ est le quotient de deux réels supérieurs à zéro, $f(x)>0\ ;\ f'(x)>0$ comme quotient de deux nombres positifs : la fonction $f$ est donc strictement croissante sur $R$ de $0$ à $2$

5. On a $f(0)=\dfrac{2}{1+1}=\dfrac{2}{2}=1$, donc $I(0\ .\ 1)\in\mathbb{C}$

La tangente à $\mathbb{C}$ au point $I$ a pour coefficient directeur $f'(0)=\dfrac{f(0)}{\mathrm{e}^{0}}=\dfrac{1}{2}$

Une entreprise souhaite fabriquer de façon automatisée des flûtes
(verres à pied) de forme allongée de   contenance $12.5\,cl$
Chaque flûte est composée de deux parties comme sur l'illustration ci-dessous :

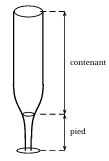
un pied, en verre plein, et un contenant de $12.5\,cl$

À l'aide de la fonction $f$ définie dans la partie $A$, le fabricant modélise
le profil du contenant de la flûte de la manière décrite ci-dessous.

Soit $A$ un point de $\mathbb{C}$ d'abscisse $\alpha$ strictement positive.

La rotation au tour de l'axe des abscisses appliquée à la partie de $\mathbb{C}$ limitée par les points $I$ et $A$ engendre une sur face modélisant le contenant de
la flûte en prenant pour unité $1\,cm.$

Ainsi $x$ et $f(x)$ représentent des longueurs en centimètres et l'objectif de cette partie est de déterminer la valeur de a pour que le volume du contenant soit égal à $12.5\,cl$

Le réel a étant strictement positif,on admet que le volume $V(\alpha)$ de ce solide en $cm^{3}$ est donné par la formule : $V(\alpha)=\pi\int_{0}^{\alpha}(f(x))^{2}dx.$

1. $\begin{array}{rcl}4\left(\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}+\dfrac{-\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}}\right)&=&4\left(\dfrac{\mathrm{e}^{x}\left(\mathrm{e}^{x}+1\right)-\mathrm{e}^{x}}{\left(\mathrm{e}+1\right)^{2}}\right)\\&=&4\left(\dfrac{\mathrm{e}^{2x}+\mathrm{e}^{x}-\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}}\right)\\&=&4\left(\dfrac{\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}}\right)\\&=&4\left(\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}\right)^{2}\\&=&\left(\dfrac{2\mathrm{e}^{x}}{\mathrm{e}^{x}+1}\right)^{2}\\&=&(f(x))^{2}\end{array}$

2.On détermine une primitive sur $\mathbb{R}$ de chaque fonction: $g$ : $x\longmapsto\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}$ et $h$ : $x\longmapsto\dfrac{-\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)^{2}}$

Si $u(x)=\mathrm{e}^{x}+1$, alors $u'(x)=\mathrm{e}^{x}$ :

$\bullet\ $ on a $g(x)=\dfrac{u'(x)}{u(x)}$ qui a pour primitive $x\longmapsto\ln|u(x)|$

Or,pour tout $x$, $\mathrm{e}^{x}+1>0$,donc la fonction $g$ a pour primitive la fonction $x\longmapsto\ln\left(\mathrm{e}^{x}+1\right)$;
 
$\bullet\ $ on a $h(x)=\dfrac{-u'(x)}{(u(x))^{2}}$ qui a pour primitive $x\longmapsto\dfrac{1}{u(x)}$

Donc la fonction $h$ a pour primitive la fonction $x\longmapsto\dfrac{1}{\mathrm{e}^{x}+1}$

3. D'après les résultats précédents:

$\begin{array}{rcl} V(\alpha)&=&\pi\int_{0}^{\alpha}(f(x))^{2}dx\\&=&\pi\int_{0}^{\alpha}4\left(\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}+\dfrac{-\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+\right)^{2}}\right)dx\\&=&\pi\int_{0}^{\alpha}4\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}dx+\pi\int_{0}^{\alpha}4\dfrac{-\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)}dx\\&=&\pi\left[4\ln\left(\mathrm{e}^{x}+1\right)\right]_{0}^{\alpha}+\pi\left[4\dfrac{1}{\mathrm{e}^{x}+1}\right]_{0}^{\alpha}\\&=&4\pi\ln\left(\mathrm{e}^{\alpha}+1\right)-4\pi\ln 2+\dfrac{4\pi}{\mathrm{e}^{\alpha}+1}-4\pi\dfrac{1}{2}\\&=&4\pi\left[\ln\left(\dfrac{\mathrm{e}^{\alpha}+1}{2}\right)+\dfrac{1}{\mathrm{e}^{\alpha}+1}-\dfrac{1}{2}\right] \end{array}$

4. On cherche une valeur approchée de $\alpha$ à $0.1$ près, sachant qu'une flûte doit contenir $12.5\,cL.$ donc $125\,cm^{3}$

La calculatrice donne $V(11.1403)\approx 125$ ; donc $\alpha\approx 11.1$ à $10^{-10}$ près.

Un client commande un lot de $400$ flûtes de $12.5\,cL$ et constate que $13$ d'entre elles ne sont pas conformes aux caractéristiques annoncées par le fabricant.

Le responsable des ventes lui avait pour
tant affirmé que $98\%$ des flûtes vendues par l'entreprise était conforme.

La fréquence de flûtes conformes est $p=0.98$

$n=400\geq 30\;,np=392\geq 5$ et $n(1-p)=9\geq 5$ donc on peut établir un intervalle de fluctuation

asymptotique eu risque de $5\%$

$\begin{array}{rcl} I_{400}&=&\left[P-1.96\dfrac{\sqrt{P(1-p)}}{\sqrt{n}}\ ;\ p+1.96\dfrac{\sqrt{p(1-p)}}{\sqrt{n}}\right]\\&=&\left[0.98-1.96\dfrac{\sqrt{0.98\times 0.02}}{20}\ ;\ 0.98+1.96\dfrac{\sqrt{0.98\times 0.02}}{20}\right]\\&\approx&[0.966\ ;\ 0.994] \end{array}$

Avec $13$ flûtes non conformes, la proportion de flûtes conformes est $\dfrac{397}{400}=0.9675$

Comme $0.9675\in[0.966\ ;\ 0.994]$ ,le client ne peut pas mettre en doute l'affirmation du responsable.

Une machine fabrique des boules destinées à un jeu de hasard.

La masse en grammes, de chacune de ces boules peut-être modélisée par une variable aléatoire M
 suivant une loi normale d'espérance $52$ et d'écart type $\delta$
 
Les boules dont la masse est comprise entre $51$ et $53$ grammes sont dites conformes.

1. Avec les réglages initiaux de la machine on a $\delta=0.437$

La probabilité qu'une boule fabriquée par cette machine soit conforme est $0.978$ au millième
près, soit $1$ à $10^{-1}$ près.

2. On considère que la machine est correctement réglée si au moins $99\%$ des boules qu'elle fa
brique sont conformes.

Déterminer une valeur approchée de la plus grande valeur de $\delta$ qui permet d'affirmer que la
machine est correctement réglée revient à trouver $\delta$ tel que $P\left(51\leq M\leq 53\right)\geq 0.99$

Considérons la variable aléatoire $Y$ telle que $Y=\dfrac{M-52}{\delta}$ qui suit  donc la loi normale centrée réduite et on a donc

$\begin{array}{rcl} P(51<M<53)=0.99&\Longleftrightarrow&P\left(-1\leq M-52\leq 1\right)\geq 0.99\\&\Longleftrightarrow&P\left(\dfrac{-1}{\delta}\leq \dfrac{M-52}{\delta}\leq \dfrac{1}{\delta}\right)\geq 0.99\\&\Longleftrightarrow&2P\left(y\leq \dfrac{1}{\delta}\right)\geq 0.99\
\\&\Longleftrightarrow&2P\left(Y\leq\dfrac{1}{\delta}\right)\geq 1.99\\&\Longleftrightarrow&P\left(Y\leq\dfrac{1}{\alpha}\right)\geq 0.995 \end{array}$

La calculatrice donne $\dfrac{1}{\delta}\geq 2.5758$ soit $\delta 0.388$

La plus grande valeur de sigma est donc $0.388$ au millième près.

La pesée des boules se fait sur des balances électroniques de précision.

Chaque jour, on vérifie que la balance n'est pas déréglée.

La durée, en jour, d'utilisation de ces balances avant dérèglement est modélisée par une variable aléatoire $T$ qui suit une loi exponentielle de paramètres $\lambda$

La courbe représentative de la fonction densité de cette variable aléatoire $T$ est donnée ci-dessous

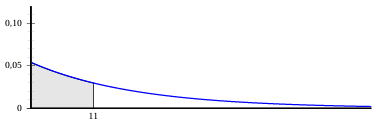
a. On sait que la fonction densité est définie par $f(t)=\lambda\mathrm{e}^{-\lambda t}$ ; donc
On lit sur la figure: $0.05<\lambda <0.06$

b. L'aire du domaine grisé, en unité d'aire, est égale à $0.45$ et correspond à $P\left(M\leq 11\right)$

On sait que l'aire est égale, en unité d'aire, à l'intégrale de la fonction densité sur l'intervalle $[0\ ;\ 11]$, soit :

$\begin{array}{rcl} 0.45&=&\int_{0}^{11}\lambda\mathrm{e}^{-\lambda t}dt\\&=&\left[-\mathrm{e}^{-\lambda t}\right]_{0}^{11}\\&=&-\mathrm{e}^{-11\lambda}-(-)\Longleftrightarrow\,0.45\\&=&1-\mathrm{e}^{-11\lambda}\Longleftrightarrow 0.55\\&=&\mathrm{e}^{-11\lambda} \end{array}$

soit, par croissant de la fonction logarithme népérien

$\begin{array}{rcl} \ln 0.55&=&-11\lambda\Longleftrightarrow\lambda\\&=&\dfrac{\ln 0.55}{-11}\\&=&-\dfrac{\ln 0.55}{11}\\&\approx&0.054349\\À&\approx&0.054 \end{array}$ au millième près.

Dans la suite, on prendra $\lambda=0.054$

2. La durée moyenne d'utilisation d'une balance sans qu'elle ne se dérègle est :

$E(T)=\dfrac{1}{\lambda}\approx\dfrac{1}{0.054}\approx 18.51$ soit environs $19$ (jours)

Une balance est mise en service le $1er$ janvier $2020.$

Elle fonctionne sans se dérégler du $1er$ au $20$ janvier inclus.

La probabilité qu'elle fonctionne sans se dérégler jusqu'au $31$ janvier inclus est :

$\begin{array}{rcl} P_{p\left(T\geq 20\right)}\left(T\geq 20+11\right)&=&P\left(T\geq 11\right)\\&=&\mathrm{e}^{-11\lambda}\\&\approx&\mathrm{e}^{-11\times 0.054}\\&\approx& 0.552 \end{array}$

On dispose de deux urnes $U$ et $V$ contenant des boules fabriquées comme précédemment.
Sur chacune des boules est inscrit l'un des nombres $-1$,$1$,ou $2$

L'urne $U$ contient une boule portant le nombre $1$ et trois boules portant le nombre $-1$

L'urne $V$ contient une boule portant le nombre $1$ et trois boules portant le nombre $2$

On considère un jeu lequel chaque partie se déroule de la manière suivante: dans un premier temps
on tire au hasard une boule dans l'urne $U$ ,on note $x$ le nombre inscrit sur cette boule puis on la met dans l'urne $V$ Dans un deuxième temps,on tire au hasard une boule dans l'urne $V$ et on note $y$ le nombre inscrit sur cette boule.

On considère les évènements suivants

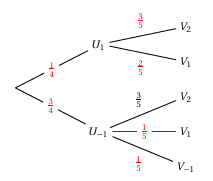
$\bullet\ U_{1}$ « on tire une boule portant le nombre $1$ dans l'urne $U$,c'est-à-dire $x=1$  »;

$\bullet\ U_{-1} $:« on tire une boule portant le nombre $-1$ dans l'urne $U$ c'est-à-dire $x=-1$ » ;

$\bullet\ V_{2}$ :« on tire une boule portant le nombre $2$ dans l'urne $V$ c'est-à-dire $y=2$ » ;

$\bullet\ V_{1}$ :« on tire une boule portant le nombre $1$ dans l'urne $V$ c'est-à-dire $y=1$ » ;

$\bullet\ V_{-1}$ :« on tire une boule portant le nombre $-1$ dans l'urne $V$ »,c'est-à-dire $y=-1$ ».

1. On complète l'arbre pondéré

2. Dans ce jeu,à chaque partie on associe le nombre complexe $z=x+iy$

On calcule les probabilités des évènements suivants.

a. $A :<<z=-1-i>>$ ;

Cela signifie que $x=-1$ et $y=-1$, donc que

$\begin{array}{rcl} P(A)&=&P\left(U_{-1}\cap V_{-1}\right)\\&=&P\left(U_{-1}\right)\times P_{U-1}\left(V_{-1}\right)\\&=&\dfrac{3}{4}\times \dfrac{1}{5}\\&=&\dfrac{3}{20}\\&=&\dfrac{15}{100}\\&=&0.15 \end{array}$

b. $B$ << $z$ et solution de l'équation $t^{2}+2t+5=0$>> ;

Avec $\Delta=4-20=-16=(4i)^{2}<0$, on sait qu'il y a deux solutions complexes :

$z_{1}=\dfrac{-2+4i}{2}=-1+2i$ et $z_{2}=\dfrac{-2-4i}{2}=-1-2i$

Dans le première cas : $x=-1$ et $y=2$ et dans le second $x=-1$ et $y=-2$ ce qui n'arrive pas.

On a donc $\begin{array}{rcl} P(B)&=&P\left(U_{-1}\cap V_{-1}\right)\\&=&P\left(U_{-1}\right)\times\left(V_{-1}\right)\\&=&\dfrac{3}{4}\times \dfrac{1}{5}\\&=&\dfrac{15}{100}\\&=&0.15 \end{array}$

c.$C$ :« Dans le plan complexe rapporté à un repère orthonormal $\left(O\ ;\ \vec{u}\;,\vec{v}\right)$ le point $M$ d'affixe $z$ appartient au disque de centre $0$ et de rayon $2$ ».
 
Les coordonnées $(x\ ;\ y)$ d'un point M du disque vérifient $x^{x}+y^{2}\leq 4$

$\bullet\ $si $x=1$ et $y=1$, alors $x^{2}+y^{2}=2\leq 4$ ; $P\left(U_{1}\cap V_{1}\right)=\dfrac{1}{4}\times \dfrac{2}{5}=\dfrac{2}{20}$

$\bullet\ $si $x=-1$ et $=-1$, alors $x^{2}+y^{2}=2\leq 4$ ; $P\left(U_{-1}\cap V_{-1}\right)=\dfrac{3}{4}\times \dfrac{1}{5}=\dfrac{3}{20}$

$\bullet\ $si $x=-1$ et $y=1$, alors $x^{2}+y^{2}=2\leq 4$ ; $P\left(U_{-1}\cap V_{-1}\right)=\dfrac{3}{4}\times \dfrac{1}{5}=\dfrac{3}{20}$

Conclusion : $P(C)=\dfrac{2}{20}+\dfrac{3}{2}+\dfrac{3}{20}=\dfrac{8}{20}=\dfrac{2}{5}$

3. Lors d'une partie,on obtient le nombre $1$ sur chacune des boules tirées.

On va montrer que le
nombre complexe $z$ associé à cette partie vérifie $z^{2020}=-2^{1010}$

On peut écrire $z$ sous la forme : $z=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+i\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}\left(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\right)=\sqrt{2}\mathrm{e}^{i\dfrac{\pi}{4}}$

Il en résulte que : $z^{2020}=\left(\sqrt{2}\mathrm{e}^{i\dfrac{\pi}{4}}\right)^{2020}=\left(\sqrt{2}\right)^{2020}\times\left(\mathrm{e}^{i\dfrac{\pi}{4}}\right)^{2020}$

$\begin{array}{rcl} \left(\sqrt{2}\right)^{2020}&=&\left(\sqrt{2}\right)^{2\times 1010}\\&=&\left(\sqrt{2}^{2}\right)^{1010}\\&=&2^{1010} \end{array}$

$\begin{array}{rcl} \left(\mathrm{e}^{i\dfrac{\pi}{4}}\right)^{2020}&=&\mathrm{e}^{i\dfrac{2020 \pi}{4}}\\&=&\mathrm{e}^{505 i\pi}\\&=&\mathrm{e}^{i \pi}\times\mathrm{e}^{504 i\pi}\\&=&-1\times\left(\mathrm{e}^{2 i\pi}\right)^{252}\\&=&-1\times 1^{252}\\&=&-1 \end{array}$

Finalement : $z^{2020}=-2^{1010}$

L'espace est rapporté à un repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\;,\vec{k}\right)$

On considère les points $A(1\ ;\ 1\ ;\ 4)$ ; $B(4\ ;\ 2\ ;\ 5)$ ; $C(3\ ;\ 0\ ;\ -2)$ et $J(1\ ;\ 4\ ;\ 2)$

On note $\bullet\ \mathbb{P}$ le plan passant par les points $A$, $B$ et $C$ ;

$\bullet\ \mathbb{D}$ La droite passant par le point $J$ et de vecteur directeur $\vec{u}\begin{pmatrix}
1\\ 1\\ 3 \end{pmatrix}$

1. Position relative de $\mathbb{P}$ et de $\mathbb{D}$

a. On montrer que la vecteur $\overrightarrow{n}\begin{pmatrix} 1\\ -4\\ 1 \end{pmatrix}$ est normal à $\mathbb{P}$

On a $\overrightarrow{AB}\begin{pmatrix} 3\\ 1\\ 1 \end{pmatrix}$ ; $\overrightarrow{AC}\begin{pmatrix}
2\\ -1\\ -6 \end{pmatrix}$

$\bullet\ \overrightarrow{AB}\cdot\overrightarrow{n}=3-4+1=0$ : les vecteurs sont orthogonaux ;

$\bullet\ \overrightarrow{AC}\cdot\overrightarrow{n}=2+4-6=0$ : Les vecteurs sont orthogonaux.

le vecteur $\overrightarrow{n}$, orthogonal à deux vecteurs manifestement non colinéaires du plan $(ABC)$,
est donc un vecteur normal à ce plan.

On détermine une équation cartésienne du plan $\mathbb{P}$

Le vecteur $\overrightarrow{n}$ est normal au plan $(ABC)$ donc le plan $(ABC)$ a une équation de la forme

$x-4y+z+d=0$, avec $de\in\mathbb{R}$

$A(1\ ;\ 1\ ;\ 4)\in(ABC)$ donc $1-4+4+d=0\Longleftrightarrow\,d =-1$

Donc le plan $'ABC)$ a pour équation : $x-4y+z-1=0$

c. On va montrer que $\mathbb{D}$ est parallèle à $\mathbb{P}$

$\vec{u}\cdot\overrightarrow{n}=1-4+3=0$ : les vecteurs $\vec{u}$ $(\text{vecteur directeur de }\mathbb{D}$ et $\overrightarrow{n}$ $\text{(vecteur normal à }\mathbb{P})$

sont orthogonaux ce qui montre que $\mathbb{D}$ est parallèle à $\mathbb{P}$ $\overrightarrow{n}$ $\text{(vecteur normal à }\mathbb{P})$

On rappelle que, un point $I$ et un nombre réel strictement positif $r$ étant donnés, la sphère de centre $I$ et de rayon $r$ est l'ensemble des points $M$ de l'espace vérifiant $IM=r$

On considère le point $I(1\ ;\ 9\ ;\ 0)$ et on appelle $\mathbb{S}$ la sphère de centre $I$ et de rayon $6.$

2. Position relative de $P$ et de $S$

a. On va montrer que la droite $\Delta$ passant par $I$ est orthogonale au plan P coupe ce plan $\mathbb{P}$ au point$H(3\ ;\ 1\ ;\ 2)$

La droite $\Delta$ passant par $I$ et orthogonale au plan $\mathbb{P}$ a donc pour vecteur directeur $\overrightarrow{n}$

Donc $M(x\ ;\ y\ ;\ z)\in\Delta\Longleftrightarrow\overrightarrow{IM}=\alpha\overrightarrow{N}\;,\alpha\in\mathbb{R}$, soit :

$\begin{array}{rcl} M(x\ ;\ y\ ;\ z)\in\Delta&\Longleftrightarrow&\left\lbrace\begin{array}{rcl} x-1&=&\alpha\\
y-9&=&-4\alpha\\ z-0&=&\alpha \end{array}\right.\\&\Longleftrightarrow&\left\lbrace\begin{array}{rcl}
x&=&1+\alpha\\ y&=&9-4\alpha\;,\quad \alpha\in\mathbb{R}\\ z&=&\alpha \end{array}\right. \end{array}$

Le point d'intersection $H$ de $\Delta$ et de $\mathbb{P}$ a ses coordonnées qui vérifient les équations de la droite et celle du plan, soit le système : $\left\lbrace\begin{array}{rcl}
x&=&1+\alpha\\ y&=&9-4\alpha\\ z&=&\alpha\\ x-4y+z-1&=&0 \end{array}\right.$

On a donc $(1+\alpha)-4(9-4\alpha)+\alpha-1=0$ ce qui équivaut $\alpha=2$

$x=1+\alpha=3$, $y=9-4\alpha=1$ et $z=\alpha=2$ donc le point $H$ a pour coordonnées $(3\ ;\ 1\ ;\ 2)$

b. On admet que pour point $M$ du plan $\mathbb{P}$ on a $IM\geq IH$

c. La sphère $\mathbb{S}$ a pour centre $I$ et la distance $IH$ du centre au plan $\mathbb{P}$ est $6\sqrt{2}$ qui est supérieure au rayon $r=6$ de la sphère.

Donc le plan $\mathbb{P}$ ne coupe pas la sphère $\mathbb{S}$

3. Position relative de $\mathbb{D}$ et de $\mathbb{S}$

a. On détermine une représentation paramétrique de la droite $\mathbb{D}$,passant par $J$ et de vecteur directeur $\vec{u}\ldots$

$\begin{array}{rcl} M(x\ ;\ y\ ;\ z)\in\mathbb{D}&\Longleftrightarrow&\overrightarrow{JM}=t\vec{u}\\&\Longleftrightarrow&\left\lbrace\begin{array}{rcl} x-1&=&t\\ y-4&=&t\\\quad\;,t\in\mathbb{R}\;,\text{soit }\ :\  z-2&=&3t \end{array}\right. \end{array}$

$M(x\ ;\ y\ ;\ z)\in\mathbb{D}\Longleftrightarrow\left\lbrace\begin{array}{rcl} x&=&1+t\\
y&=&4+t\;,t\in\mathbb{R}\\ z&=&2+3t \end{array}\right.$

b. $\begin{array}{rcl} M(x\ ;\ y\ ;\ z)\in\mathbb{S}&\Longleftrightarrow&IM=6\\&\Longleftrightarrow&IM^{2}\\&=&36\\&\Longleftrightarrow&(x-1)^{2}+(y-(-4))^{2}+(z-0)^{2}\\&=&36\\&\Longleftrightarrow&(x-1)^{2}+(y-9)^{2}+z^{2}\\&=&36 \end{array}$

c. On a $\begin{array}{rcl}a IJ^{2}=(1-1)^{2}+(9-4)^{2}+(2-0)^{2}\\&=&25+4\\&=&29 \end{array}$

Donc $IJ=\sqrt{29}\approx5.4<6$ longueur du rayon de la sphère : ceci montre que $J$ est  intérieur à la sphère et donc toute droite contenant $J$ coupe la sphère en deux points

Pour les candidats n'ayant pas suivi l'enseignement de spécialité
 
On considère la suite $\left(u_{n}\right)$ définie, pour tout entier naturel non nul $n$, par : $u_{n}=\dfrac{n(n+2)}{n+1)^{2}}$

La suite $\left(V_{2}\right)$ est définie par

$v_{1}=u_{1}\;,u_{1}\times u_{2}$ et pour tout entier naturel $n\geq 3\;, v_{n}=u_{1}\times u_{2}\times\ldots\times u_{n}=v_{n-1}\times u_{n}$

1. $\begin{array}{rcl} u_{1}&=&\dfrac{3}{4}\\&\text{ et }u_{2}\\&=&\dfrac{8}{9}\;,\\&\text{donc }&v_{2}\\&=&\dfrac{3}{4}\times \dfrac{8}{9}\\&=&\dfrac{3\times 4\times 2}{4\times \times 3\times 3}\\&=&\dfrac{2}{3}
\end{array}$

2. $\begin{array}{rcl} u_{3}&=&\dfrac{15}{16}\;,\\&\text{ donc }v_{3}\\&=&u_{1}\times u_{2}\times u_{3}\\&=&v_{2}\times v_{3}\\&=&\dfrac{2}{3}\times \dfrac{15}{16}\\&=&\dfrac{5}{8} \end{array}$

On complète l'algorithme ci-contre afin que, après son exécution, la variable $V$ contiennent la valeur $v_{n}$ où $n$ est
un nombre entier naturel non nul défini par l'utilisateur.

$\begin{array}{rcl} \hline\\ \text{Algorithme}\\ 1. V\longleftarrow\, 1\\2. \text{ pour }i\text{ variant de }1\text{ à }n\\ 3. U\longleftarrow\dfrac{i(i+2)}{(i+1)^{2}}\\ 4. V\longleftarrow V\times U\\ 5. \text{Fin Pour}\\ \hline \end{array}$

3.a. On a, quel que soit $n\in\mathbb{N}$

$\begin{array}{rcl} u_{n}&=&\dfrac{n(n+2)}{(n+1)^{2}}\\&=&\dfrac{n^{2}+2n}{(n+1)^{2}}\\&=&\dfrac{n^{2}+2n+1-1}{(n+1)^{2}}\\&=&\dfrac{(n+1)^{2}}{(n+1)^{2}}-\dfrac{1}{(n+1)^{2}}\\&=&1-\dfrac{1}{(n+1)^{2}}
\end{array}$

b. De par sa définition $u_{n}$ quotient de deux termes supérieurs à $0$ est supérieur à $0$

D'après la question précédente comme $\dfrac{1}{(n+1)^{2}}>0$, $1-\dfrac{1}{(n+1)^{2}}<1$, soit $u_{n}<1$, quel que soit $n\in\mathbb{N}^{\ast}$

Conclusion : pour $n\in\mathbb{N}$, $0<u_{n}<1$

4. a. Quel que soit $\begin{array}{rcl} n\;,\dfrac{v_{n}+1}{v_{n}}&=&\dfrac{u_{1}\times \ldots\times u_{n}\times u_{n+1}}{u_{1}\times\ldots\times u_{n}}\\&=&u_{n+1} \end{array}$

Or d'après la question précédente $u_{n+1}<1$, donc $\dfrac{v_{n+1}}{v_{n}}<1$, donc la suite $\left(v_{n}\right)$ est décroissante

Les termes un étant supérieurs à zéro, les termes $v_{n}$ sont supérieurs à zéro.

On a donc quel que soit$n\in\mathbb{N}^{\ast}\;,0<v_{n}$

La suite $\left(v_{n}\right)$ est donc décroissante et minorée par $0$; d'après le théorème de la convergence monotone, elle est convergente vers un réel supérieur ou égal à zéro.

5.a. $\begin{array}{rcl} v_{n+1}&=&v_{n}\times u_{n+1}\\&=&v_{n}\times\dfrac{(n+1)(n+3)}{(n+2)^{2}}
\end{array}$

b. Soit la propriété : $v_{n}\dfrac{n+2}{2(n+1)}$

$\bullet\ $Initialisation

$v_{1}=u_{1}=\dfrac{3}{4}$ et $\dfrac{1+2}{2\times 2}=\dfrac{3}{4}$ : la relation est vraie au rang $1$

$\bullet\ $Hérédité

Soit $n\in\mathbb{N}$ tel que $n\geq 1$ et supposons que $v_{n}=\dfrac{n+2}{2(n+1)}$

D'après la question précédente :

$\begin{array}{rcl} v_{n+1}&=&v_{n}\times\dfrac{(n+1)(n+3)}{(n+2)^{2}}\\&=&\dfrac{n+2}{2(n+1)}\times\dfrac{(n+1)(n+3)}{n+2)^{2}}\\&=&\dfrac{n+3}{2(n+3)}\\&=&\dfrac{(n+1)+2}{2(n+1)+1)} \end{array}$

La relation est vraie au rang $n+1$

$\bullet\ $Conclusion

 2((n+1)+1) ;
 
La relation est vraie au rang $1$ et si elle est vraie à un rang au moins égal à 1$1$, elle est vraie au rang suivant ; d'après le principe de récurrence : pour tout entier naturel non nul $n$, $v_{n}=\dfrac{n+2}{2(n+1)}$

c. On peut puisque $n\neq 0$ écrire $v_{n}=\dfrac{n+2}{2(n+1)}$

Or $\lim\limits_{n\longrightarrow\,+\infty}\dfrac{2}{n}=\lim\limits_{n\longrightarrow+\infty+\infty}\dfrac{1}{n}$, donc par somme et quotient de limites : $\lim\limits_{n\longrightarrow+\infty}v_{n}=\dfrac{1}{2\times }\dfrac{1}{2}$
 
6. On considère la suite $w_{n}$ définie par

$w_{1}=\ln\left(u_{1}\right)$, $w_{2}=\ln\left(u_{1}\right)+\ln\left(u_{2}\right)$ et, pour tout entier naturel $n\geq 3$, par

$w_{n}=\sum_{\lim _{n}^{^{k=1}}}\ln\left(u_{k}\right)=\ln\left(u_{1}\right)+\ln\left(u_{2}\right)+\ldots+\ln\left(u_{n}\right)$

On a $w_{1}=\ln\left(u_{1}\right)=\ln\left(\dfrac{3}{4}\right)$ ;

$\begin{array}{rcl}w_{7}&=&\ln\left(u_{1}\right)+\ln\left(u_{2}\right)+\ldots+\ln\left(u_{7}\right)\\&=&\ln\left(u_{1}\times u_{2}\times\ldots\times u_{7}\right)\\&=&\ln\left(v_{7}\right)
\end{array}$ soit d'après le résultat de la question $5.c$ $w_{7}=\ln\dfrac{7+2}{2(7+1)}=\ln\dfrac{9}{16}$

Or $\dfrac{9}{16}=\left(\dfrac{3}{4}\right)^{2}$, donc : $w_{7}=\ln\left(\dfrac{3}{4}\right)^{2}=2\ln\dfrac{3}{4}=2w_{1}$

Pour les candidats ayant suivi l'enseignement de spécialité

Pour tout entier naturel $n$, on définit les entiers $a_{n}=6\times 5^{n}-2$ et $b_{n}=3\times 5^{n}+1$

1.a $\begin{array}{rcl}5\equiv 1[4]\\&\text{ donc }& 5^{n}\\&\equiv& 1^{n}[4]\\&\text{ donc }&5^{n}\\&\equiv 1[4] \end{array}$

$\bullet\ $ $\begin{array}{rcl} 6\times 5^{n}&\equiv& 6\times 1\\&\equiv& 6[4]\\&\text{ donc }&6\times 5^{n}-2\\&\équiv&6-2\\&\equiv&0[4]\\&\text{ donc }&\alpha_{n}\\&\equiv&0[4] \end{array}$