Corrigé du baccalauréat S Antilles-Guyane - 9 septembre 2020
Exercice 1
Partie A
1. On traduit cette situation à l'aide de l'arbre pondéré suivant :
2. En utilisant l'arbre pondéré précédent, on obtient :
$P(M\cap S)=0.55\times 0.7\approx 0.385$
La probabilité que Louise emmène Zoé le matin et qu'elle la ramène le soir est à peu près égale à $0.385$
3. $\begin{array}{rcl} P(S)&=&P(M\cap S)+P\left(M\cap \overline{S}\right)\\&=&0.385+0.45\times 0.24\\&\approx& 0.493 \end{array}$
4. Il s'agit de calculer $Ps(M)$
$\begin{array}{rcl} Ps(M)&=&\dfrac{P\left(M\cap S\right)}{P(S)}\\&=&\dfrac{0.385}{0.493}\\ &\approx&0.781 \end{array}$
Partie B
$X$ qui suit la loi normale d'espérance $28$ et d'écart-type $5$
En utilisant la calculatrice, on obtient les résultats suivants :
1. $P\left(X\leq 25\right)\approx0.274$
2. $P\left(18\leq x\leq 38\right)\approx 0.954$
3. $P\left(x\geq d\right)=0.1$, on obtient $d\approx 34$
La durée du trajet (arrondie à la minute), telle que $P(X\geq d)=0.1$ est de $34$ minutes.
4. $Y$ suit la loi normale d'espérance $26$ et d'écart-type $\sigma$ alors $Z=\dfrac{Y-26}{\sigma}$ suit la loi normale d'espérance $0$ et d'écart type $1$
On sait que $P\left(Y\geq 30\right)=0.1$
$\begin{array}{rcl} P(Y\geq30)=0.1&\Longleftrightarrow&P\left(Y-26\geq 30-26\right)=0.1\\&\Longleftrightarrow&P\left(\dfrac{Y-26}{\sigma}\geq\dfrac{4}{\sigma}\right)=0.1 \\&\Longleftrightarrow&P\left(z\geq\dfrac{4}{\sigma}\right)=0.1 \end{array}$
À l'aide de la calculatrice on trouve 4 $\dfrac{4}{\sigma}\approx 1.281$ d'où $\sigma\approx\dfrac{4}{1.281}\approx 3.12$
Partie C
Ici on interroge $N=254$ salariés de manière indépendante.
La proportion annoncée des salariés pratiquant le covoiturage est $P=0.35$
On a $N\geq 30$ , $Np=88.9\geq 5$ et $n(1-p)=165.1\geq 5$
On peut donc établir un intervalle de fluctuation asymptotique au seuil de $95\%$
$I_{N}=\left[p-1.96\dfrac{\sqrt{p(1-p)}}{\sqrt{N}}\ ;\ p+1.96\dfrac{\sqrt{p(1-p)}}{\sqrt{N}}\right]$
Or $p-196\dfrac{\sqrt{p(1-p)}}{\sqrt{N}}\approx 0.291$ et $p+1.96\dfrac{p(1-p)}{\sqrt{N}}\approx0.409$ donc $I_{N}=[0.291\ ;\ 0.409]$
La fréquence observée est $f=\dfrac{82}{254}\approx0.323\in I_{N}$
Ce sondage ne remet pas en cause l'information publiée par l'entreprise sur son site internet
Exercice 2
Commun à tous les candidats
Partie A
La fonction $g$ est définie sur $[0\ ;\ +\infty[$ par $g(x)=1-\mathrm{e}^{-x}$
1. $\lim\limits_{x\longrightarrow+\infty}-x=-\infty$ donc $\lim\limits_{x\longrightarrow+\infty}\mathrm{e}^{-x}=0$ et $\lim\limits_{x\longrightarrow+\infty}1-\mathrm{e}^{-x}=1$
2. $g(x)=1-\mathrm{e}^{-x}$ donc $g'(x)=\mathrm{e}^{-x}$
Pour tout réel $x donc g′(x)>0 sur [0;+∞[.$
La fonction $g$ est donc strictement croissante sur $[0;+∞[$
Partie B
1.a. $f(x)=(x-1)\mathrm{e}^{-kx}+1$
$u(x)=x-1\quad\quad v(x)=\mathrm{e}^{-kx}$
$u'(x)=1\quad\quad v'(x)=-ke^{-kx}$
$f=uv+1$ et $(uv)'=u'v+uv'$
$f'(x)=1\times \mathrm{e}^{-kx}+(x-1)\times\left(k\mathrm{e}^{-kx}\right)+0=\mathrm{e}^{-kx} (1+(x-1)(-k))=\mathrm{e}^{-kx}(1-kx+k)=\mathrm{e}^{-kx}(-kx+k+1)$
b. La tangente $T$ a pour équation $y=f'(1)(x-1)+f(1)$
or $f(1)=1$ et $f'(1)=\mathrm{e}^{-k}$
Donc $T$ a pour équation $y=f'(1)(x-1)+1=\mathrm{e}^{-k}x-\mathrm{e}^{-k}+1$
$B$ est le point de $T$ d'abscisse $0$,donc $y_{B}=-\mathrm{e}^{-k}+1=g(k)$
2.D'après le tableau de variation de la fonction $g$ de la partie $A$,pour tout réel positif $k\;,g(k)\in[0\ ;\ 1]$
Le point $B$ ayant pour coordonnée $(0\ ;\ g (k))$ avec $0\leq g(k)\leq 1$,il appartient bien au segment $[OJ]$
Partie C
La fonction $h$ est définie sur $\mathbb{R}$ par $h(x)=(x-1)\mathrm{e}^{-2x}+1$
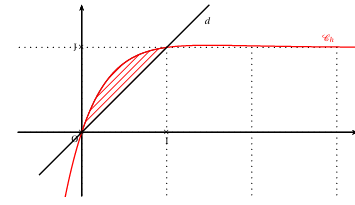
1. Voir ANNEXE 1.
Sur l'intervalle $[0\ ;\ 1]$ : la courbe $C_{h}$ est au-dessus de la droite $d$ d'équation $y=x$ donc $h(x)\geq x$,
$\mathbb{D}$ est le domaine du plan délimité par la courbe $C_{h}$ et la droite $d$
$\mathbb{A}$ est l'aire de $\mathbb{D}$ exprimée en unité d'aire, donc
$$\mathbb{A}=\int_{0}^{1}(h(x)-x)dx$$
2.a. $\begin{array}{rcl} h(x)-x&=&(x-1)\mathrm{e}^{-2x}+1-x\\&=&-(1-x)\mathrm{e}^{-2x}+(1-x)\\&=&(1-x)\mathrm{e}^{-2x}+(1+x)\\&=&(1-x)\left(-\mathrm{e}^{-2x}+1\right)\\&=&(1-x)\left(1-\mathrm{e}^{-2x}\right) \end{array}$
b. On admet que, pour tout réel $x$, $\mathrm{e}^{-2x}\geq 1-2x$
$\begin{array}{rcl} \mathrm{e}^{-2x}\geq 1-2x&\Longleftrightarrow&-\mathrm{e}^{-2x}\leq 2x-1&\Longleftrightarrow&1-\mathrm{e}^{-2x}\leq 1+2x-1&\Longleftrightarrow&1-\mathrm{e}^{-2x}\leq 2x
\end{array}$
Sur $[0\ ;\ 1]\;,x\leq 1$ donc $1-x\geq 0$ d'où
$\begin{array}{rcl} 1-\mathrm{e}^{-2x}\geq 2x&\Longleftrightarrow&(1-x)\left(1-\mathrm{e}^{-2x}\right)\geq(1-x)2x&\Longleftrightarrow&h(x)-x\geq 2x-2x^{2} \end{array}$
c. $h(x)-x\leq 2x-2x^{2}$ donc $\int_{0}^{1}(h(x)-x)dx.\leq \int_{0}^{1}\left(2x-2x^{2}\right)dx$
$\int_{0}^{1}\left(2x-2x^{2}\right)dx=\left[x^{2}-\dfrac{2}{3}x^{3}\right]_{0}^{1}=1-\dfrac{2}{3}=\dfrac{1}{3}$
on obtient donc $\mathbb{A}\leq\dfrac{1}{3}$
3. $\begin{array}{rcl} \mathbb{A}&=&\int_{0}^{1}(h(x)-x)dx\\&=&\left[H(x)-\dfrac{x^{2}}{2}\right]_{0}^{1}\\&=&H(1)-\dfrac{1}{2}-H(0)\\&=&\dfrac{1}{4}(1-2)\mathrm{e}^{-2}-\dfrac{1}{2}+1-\dfrac{1}{4}\mathrm{e}^{0}\\&=&-\dfrac{1}{4}\mathrm{e}^{-2}-\dfrac{1}{2}+1-\dfrac{1}{4}\\&=&-\dfrac{1}{4}\mathrm{e}^{-2}+\dfrac{1}{4}
\end{array}$
Exercice 3
Commun à tous les candidats
On se place dans le repère $\left(A\ ;\ \overrightarrow{AB}\;,\overrightarrow{AD}\;,\overrightarrow{AE}\right)$
1. $H(0\ ;\ 1\ ;\ 1)$, $M(0.5\ ;\ 0\ ;\ 0)$ et $N(1\ ;\ 0.5\ ;\ 0)$
2.a. La droite $(MN)$ est définie par le point $M$ et le vecteur $\overrightarrow{MN}$
$$M(0.5\ ;\ 0\ ;\ 0)\text{ et }\overrightarrow{MN}\begin{pmatrix} 0.5\\ 0.5\\ 0 \end{pmatrix}$$
Une représentation paramétrique de la droite $(MN)$ est donc :
$$\begin{array}{rcl} x&=&0.5+0.5\,k\\ y&=&0.5\,k\quad k\in\mathbb{R}\\ z&=&0 \end{array}\right.$
b. Une représentions paramétrique de la droite $(CD)$ est
$$\begin{array}{rcl} x&=&t\\ y&=&1\quad ,t\in\mathbb{R}\\ z&=&0 \end{array}$$
$K$ étant le point d'intersection des droites $(CD)$ et $(MN)$, ses coordonnées sont solutions du système
$\begin{array}{rcl}\left\lbrace\begin{array}{rcl} x&=&t\\y&=&1\\ z&=&0\\x&=&0.5+0.5k\\y&=&0.5k\\z&=&0 \end{array}\right. &\Leftrightarrow&\left\lbrace\begin{array}{rcl} 1&=&0.5k\\ t&=&0.5+0.5k\\ x&=&t\\ y&=&1\\ z&=&0 \end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} k&=&2\\ t&=&1.5\\ x&=&1.5\\ y&=&1\\ z&=&0 \end{array}\right.\end{array}$
C'est pourquoi $K(1.5\ ;\ 1\ ;\ 0)$
3.a. $\overrightarrow{HM}\begin{pmatrix} 0.5\\ -1\\ -1 \end{pmatrix}\overrightarrow{HN}\begin{pmatrix}
1\\ -0.5\\ -1 \end{pmatrix}\overrightarrow{n}\begin{pmatrix} 2\\ -2\\ 3 \end{pmatrix}$
$\overrightarrow{HM}$ et $\overrightarrow{HN}$ ne sont pas colinéaires car $\dfrac{1}{0.5}\\neq\dfrac{-0.5}{-1}$
3.a $\overrightarrow{HM}\begin{pmatrix} 0.5\\ -1\\ -1 \end{pmatrix}\overrightarrow{HN}\begin{pmatrix} 1\\
-0.5\\ -1 \end{pmatrix}\overrightarrow{n}\begin{pmatrix} 2\\ -2\\ 3 \end{pmatrix}$
$\overrightarrow{HM}$ et $\overrightarrow{HN}$ ne sont pas colinéaires car $\dfrac{1}{0.5}\neq \dfrac{-0.5}{-1}$
$\overrightarrow{n}\cdot\overrightarrow{HM}=2\times 0.5-2\times(-1)+3\times(-1)=1+2-3=0$
$\overrightarrow{n}\cdot\overrightarrow{HN}=2\times 1-2\times (-0.5)+3\times\times(-1)=2+1-3=0$
Le vecteur $\overrightarrow{n}$ est orthogonal à deux vecteurs non colinéaires du plan $(HMN)$,c'est donc un vecteur normal à ce plan.
b. $\overrightarrow{n}\begin{pmatrix} 2\\ -2\\ 3\end{pmatrix}$ étant un vecteur normal du plan $(HMN)$,
une équation cartésienne de ce planes $2x-2y+3z+d=0$, $H(0\ ;\ 1\ ;\ 1)$ appartient à ce plan donc ses
coordonnées vérifient l'équation,on a donc $2\times 0-2\times 1+3\times 1+d=0$ soit $d=-1$
Une équation du plan $(HMN)$ est donc $2x-2y+3z-1=0$
c. Déterminons une représentation paramétrique de la droite $(CG.)$
Cette droite est déterminée par le point
$C(1\ ;\ 1\ ;\ 0)$ et $\overrightarrow{CG}\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}$
Une représentation paramétrique de la droite $(MN)$ est donc:
$\left\lbrace\begin{array}{rcl} x&=&1\\ y&=&1\;,p\in\mathbb{R}\\ z&=&p \end{array}\right.$
$L$ est le point d'intersection de la droite $(CG)$ et du plan $(HMN)$,ses coordonnées sont donc solutions du système suivant:
C'est pourquoi $L(1\ ;\ 1\ ;\ ;\ \dfrac{1}{3})$
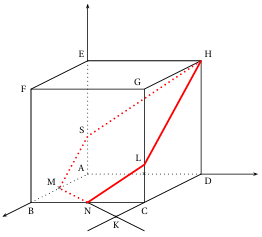
4. Sur la face $(ABCD)$,on trace le segment $[MN]$,sur la face $(BCGF)$,on trace le segment $[NL]$,sur la face $(CDHG)$,on trace le segment $[LH]$,
Les faces $(ABFE)$ et $(CDHG)$ sont parallèles donc les droites d'intersection des ces deux plans avec le plan $(HMN)$
sont parallèles.
On trace la parallèle à $(LHp)$ Passant par $M$,elle coupe la droite $(AE)$ en un point $S$
Sur la face $(ADHE)$,on trace le segment $[SH]$,(on peut remarquer que $(SH)$ est parallèle à $(NL)$
La section du cube par le plan $(HMN)$ est donc $MNLHS$
Voir annexe $2$
Exercice 4
Candidats n'ayant pas suivi l'enseignement de spécialité
1. $u_{0}=4$ et pour tout entier naturel $n$, $u_{n+1}=-\dfrac{2}{3}u_{n+1}$ et $v_{n}=u_{n}-\dfrac{2}{3}$
$u_{0}=4$
$u_{1}=-\dfrac{2}{3}\times 4+1=-\dfrac{8}{3}+1=-\dfrac{5}{3}$
$u_{2}=-\dfrac{2}{3}\times(-\dfrac{5}{3})+1=-\dfrac{19}{9}$
$\dfrac{v_{1}}{v_{0}}=\dfrac{-\dfrac{7}{3}}{\dfrac{10}{3}}=-\dfrac{7}{3}\times\dfrac{3}{10}=-\dfrac{7}{10}$
$v_{0}=4-\dfrac{2}{3}=\dfrac{10}{3}$
$v_{1}=-\dfrac{5}{3}-\dfrac{2}{3}=-\dfrac{7}{3}$
$v^{1}_{2}=\dfrac{19}{9}-\dfrac{2}{3}=\dfrac{13}{9}$
$\dfrac{v_{2}}{v_{1}=\dfrac{\dfrac{13}{9}}{-\dfrac{7}{3}}}=-\dfrac{13}{9}\times \dfrac{3}{7}=-\dfrac{13}{21}$
$\dfrac{v_{1}}{v_{2}}\neq \dfrac{v_{2}}{v_{1}}$, donc $\left(v_{n}\right)$
n'est pas une suite géométrique. L'affirmation $1$ est donc fausse.
2. Pour tout entier naturel $n$ non nul,
$\begin{array}{rcl} -1\leq\cos (n)\leq 1&\Longleftrightarrow&3-1\leq 3+\cos(n)\leq 3+1\\&\Longleftrightarrow&2\leq 3+\cos(n)\leq 4\\&\Longleftrightarrow&\dfrac{2}{n^{2}}\leq \dfrac{3+\cos (n)}{n^{2}}\leq \dfrac{4}{n^{2}}\\&\text{or }&\lim\limits_{n\longrightarrow+\infty}\dfrac{2}{n^{2}} =\lim\limits_{n\longrightarrow+\infty}\dfrac{4}{n^{2}}=0 \end{array}$
d'après le théorème des gendarmes $\lim\limits_{n\longrightarrow+\infty}\dfrac{3+\cos(n)}{n^{2}}=0$, l'affirmation $2$ est donc vraie.
3. À la fin de l'exécution,la variable $U$ contient la première valeur strictement supérieur à $5000$
En effet l'algorithme ne s'arrête pas tant que $U\leq 5000$
En utilisant la calculatrice,on obtient la valeur $6565$
L'affirmation $3$ est donc fausse.
4. $(z-i)\left(z^{2}+z\sqrt{3}+1\right)=0\Longleftrightarrow(z-i)=0$ ou $\left(z^{2}+z\sqrt{3}+1\right)=0$
$(z-i)=0\longleftrightarrow z=i$
$z^{2}+z\sqrt{3}+1=0$
$\Delta=\sqrt{3}^{2}-4\times 1=-1=i^{2}$
$\Delta$ est un réel strictement négatif donc l'équation a pour solution deux nombres complexes conjugués:
$z_{1}=\dfrac{-\sqrt{3}-i}{2}$ et $z_{2}=\overline{1}=\dfrac{-\sqrt{3}+i}{2}$
L'équation $(z-i)\left(z^{2}+z\sqrt{3}+1\right)=0$ a donc comme ensemble solution : $S=\left\lbrace i\;,\dfrac{-\sqrt{3}-i}{2}\;,\dfrac{-\sqrt{3}+i}{2}\right\rbrace$
$|i|=\;,\left|\dfrac{-\sqrt{3}-i}{2}\right|=\left|\dfrac{-\sqrt{3}+i}{2}\right|=\dfrac{3+1}{4}=1$
L'affirmation $4$ est donc vraie
5. $z_{0}=2$ et pour tout entier naturel $z_{n+1}=2\mathrm{e}^{i\dfrac{\pi}{n}z_{n}}=2iz_{n}$
$z_{1}=2iz_{0}=2i\times 2=4i$
Soit $K$ le milieu du segment $\left[M_{0}M_{2}\right]$ $z_{k}=\dfrac{z_{0}+z_{2}}{2}=\dfrac{2-8}{2}=-3$
le point $O$ n'est donc pas le milieu du segment $\left[M_{o}M_{o}\right]$ ,l'affirmation $5$ est fausse.
Exercice 5
Candidats ayant suivi l'enseignement de spécialité
On considère l'équation $(E)x^{2}-5y^{2}=1$ où $x$ et $y$ sont de sentiers naturels.
Partie A
1. Si $x$ et $y$ sont deux entiers naturels paires, il existe deux entiers naturels $p$ et $q$ tels que $x=2p$ et $y=2q$
$(x\ ;\ y)$ est un couple solution de l'équation
$\begin{array}{rcl} (E)&\Longleftrightarrow&x^{2}-5y^{2}=1\\&\Longleftrightarrow&(2p)^{2}-5(2q)^{2}=1\\&\Longleftrightarrow&4p^{2}-5\times 4q^{2}=1\\&\Longleftrightarrow&4\left(p^{2}-5q^{2}\right)=1 \end{array}$
On en déduit $4$ est un diviseur de $1$,ce qui est impossible.
Donc $x$ et $y$ ne peuvent pas être tous les deux pairs.
Si $x$ et $y$ sont deux entiers naturels impairs, il existe deux entiers naturels $p$ et $q$ tels que $x=2p+1$ et $y=2q+1$
$(x\ ;\ y)$ est un couple solution de l'équation $\begin{array}{rcl} (E)&\Longleftrightarrow&x^{2}-5y^{2}=1\\&\Longleftrightarrow&(2p+1)^{2}-52q+1)^{2}=1\\&\Longleftrightarrow&4p^{2}+4p+1-5\left(4q^{2}+4q+1\right)=1\\&\Longleftrightarrow&4p^{2}+4p+1-20q^{2}-20q-5=1\\&\Longleftrightarrow&4p^{2}+4p-20q^{2}-20q-4=1\\&\Longleftrightarrow&4\left(p^{2}+p-5q^{2}-5q-1\right)=1 \end{array}$
On en déduit que $4$ est un diviseur de $1$, ce qui est impossible.
Donc $x$ et $y$ ne peuvent pas être tous les deux impairs.
En conclusion,$x$ et $y$ ne peuvent pas avoir la même parité.
2.Soit $d$ un diviseur commun à $x$ et $y$,il existe deux entiers naturels $x$ et $y$ tels que $x=dX$ et $y=dY$
$(c\ ;\ y$est un couple solution de l'équation
$\begin{array}{rcl} (E)&\Leftrightarrow&x^{2}-5y^{2}=1\&\Leftrightarrow&\left(dX\right)^{2}-5\left(dY\right)^{2}=1\\&\Leftrightarrow&d^{2}X^{2}-5\left(d^{2}-y^{2}\right)=1\\&\Leftrightarrow&d^{2}\left(X^{2}-5Y^{2}\right)=1 \end{array}$
On en déduit que $d^{2}$ est un diviseur de $1$,donc $d=1$
Le seul diviseur commun à $x$ et $y$ est $1$, $x$ et $y$ sont donc premiers entre eux.
3. Soit $k$ un entier naturel.
$\begin{array}{|c|c|c|c|c|c|} \hline \text{Reste de la division eu }&&&&&\\ \text{clidienne de }k\text{ par }5&0&1&2&3&4\\ \hline \text{Reste de la division eu-}&0&1&4&4&1\\ \text{clidienne de }k^{2}\text{ par }5&&&&&\\ \hline \end{array}$
$\left(x\ ;\ y\right)$ est un couple solution de l'équation $(E)$ donc $x^{2}=1+5y^{2}$
On en déduit que $x^{2}\equiv1[5]$,d'après le tableau précédent on a alors $x\equiv 1[5]$ ou $x\equiv 4[5]$
Partie B
1. $\begin{pmatrix} x_{n}+1\\ y_{n}+1 \end{pmatrix}=A\begin{pmatrix} x_{n}\\ y_{n} \end{pmatrix}=\begin{pmatrix} 9\quad 20\\ 4\quad 9 \end{pmatrix}\begin{pmatrix} x_{n}\\ y_{n} \end{pmatrix}$ d'où $\left\lbrace\begin{array}{rcl} x_{n+1}&=&9x_{n}+20y_{n}\\
y_{n+1}&=&4x_{n}+9y_{n} \end{array}\right.$
2.Démontrons par récurrence que, pour tout entier naturel $n$, $\left(x_{n}\;,y_{n}\right)$ est solution de l'équation $(E)$
$\bullet\ $Initialisation: $x_{0}=1$ et $y_{0}=0 $ donc $x_{0}^{2}-5y_{0}^{2}=1$
La propriété est vraie au rang $0$
$\bullet\ $ Hérédité: Supposons la propriété vraie au rang $n$, c'est-à-dire $x_{n}^{2}-5y_{n}^{2}=1$ et démontrons qu'alors elle est vraie au rang $(x+1)$,c'est à dire $x_{n+1}^{2}-5y_{n+1}^{2}=1$
$\begin{array}{rcl} \left(x_{n+1}\right)^{2}-5\left(y_{n+1}\right)^{2}&=&\left(9x_{n}+20y_{n}\right)^{2}-5\left(4x_{n}+9y_{n}\right)^{2}\\ &=&81x_{n}^{2}+360x_{n}y_{n}+400y_{n}^{2}-5\left(16x_{n}^{2}+72x_{n}y_{n}+81y_{n}^{2}\right)\\&=&81x_{n}^{2}+360x_{n}y_{n}+400y_{n}^{2}-80x_{n}^{n}-360x_{n}y_{n}-405y_{n}^{2}=x_{n}^{2}-5y_{n}^{2}=1\end{array}$
Donc la propriété est vraie au rang $(n+1)$ ;elle est héréditaire.
$\bullet\ $ Conclusion:
la propriété est vraie au rang $0$ et est héréditaire,donc,par application du principe de
récurrence,elle est vraie pour tout entier naturel $n$
3.a. $A^{2}=\begin{pmatrix} 9\quad 20\\ 4\quad 9 \end{pmatrix}\times\begin{pmatrix} 9\quad 20\\
4\quad 9 \end{pmatrix}=\begin{pmatrix} 81+80\quad 180+180\\ 36+36\quad 80+81 \end{pmatrix}=\begin{pmatrix}
161\quad 360\\ 72\quad 161 \end{pmatrix}$
$\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}=A\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}A^{2}\begin{pmatrix}
x_{0}\\ y_{0} \end{pmatrix}=\begin{pmatrix} 161\quad 360\\ 72\quad 161 \end{pmatrix}\begin{pmatrix}
1\\ 0 \end{pmatrix}$ d'où $\left\lbrace\begin{array}{rcl} x_{2}&=&161\\ y_{2}&=&72 \end{array}\right.$
b. Soit $P$ un entier naturel
$\begin{pmatrix} x_{p}+2\\ y_{p}+2 \end{pmatrix}=A\begin{pmatrix} x_{p+1}\\ y_{p+1} \end{pmatrix}=A^{2}\begin{pmatrix} x_{p}\\ y_{p} \end{pmatrix}=\begin{pmatrix} 161\quad 360\\ 72\quad 161 \end{pmatrix}\begin{pmatrix} x_{p}\\ y_{p} \end{pmatrix}$ d'où $y_{p+2}=72x_{p}+161y_{p}$
Si $y_{p}$ est multiple de $9$, il existe un entier naturel $k$ tel que $y_{p}=9k$ d'où $y_{p+2}=72x_{p}+161\times 9k=9\left(8x_{p}+161k\right)$, donc $x_{p+2}$ est bien multiple de $9$
$\bullet\ $ Initialisation : $y_{0}=0$ est bien multiple de $9$
La propriété est vraie au rang $0$
$\bullet\ $Hérédité: Supposons la propriété vraie au rang $n$,et démontrons qu'alors elle est vraie au rang $(n+1)$
$y_{2}(n+1)=y_{2}n+2$,d'après la question précédente,puis que $y2n$ est multiple de $9$,alors $y2_{n+2}$ est également multiple de $9$
Donc la propriété est vraie au rang $(n+1)$ ; elle est héréditaire.
$\bullet\ $Conclusion: la propriété est vraie au rang $0$ et est héréditaire,donc,par application du principe de récurrence,elle est vraie pour tout entier naturel $n$
$y_{2020}=y_{(2\times 1010}$ est donc un multiple de $9$

Ajouter un commentaire