Corrigé Exercice 27 : Théorème de Thalès - 3e

 

1) Construisons le triangle $ABC$ tel que : 

 

$AB=6\;cm$ ; 

 

$AC=9\;cm$ ; 

 

$BC=7\;cm.$

 

2) Construisons le point $M$ de $[BC]$ tel que : $BM=\dfrac{2}{3}BC.$

 

3) La parallèle à $(AB)$ passant par $M$ coupe $(AC)$ en $N.$

 

a) Démontrons que $\dfrac{CN}{AC}=\dfrac{1}{3}$

 

Comme les droites $(AB)\ $ et $\ (MN)$ sont parallèles alors, les triangles $ABC\ $ et $\ CMN$ sont en position de Thalès.

 

Ainsi, en utilisant le théorème de Thalès, on a :

$$\dfrac{CN}{AC}=\dfrac{CM}{BC}$$

Or, on sait que : $CM=BC-BM$

 

Comme $BM=\dfrac{2}{3}BC$ alors, on a :

 

$\begin{array}{rcl} CM&=&BC-\dfrac{2}{3}BC\\\\&=&\left(1-\dfrac{2}{3}\right)BC\\\\&=&\dfrac{3-2}{3}BC\\\\&=&\dfrac{1}{3}BC\end{array}$

 

Donc, $CM=\dfrac{1}{3}BC$

 

Ainsi, en remplaçant $AC\;,\ CM\ $ et $\ BC$ par leur valeur, on obtient :

 

$\begin{array}{rcl}\dfrac{CN}{AC}=\dfrac{CM}{BC}&\Leftrightarrow&\dfrac{CN}{AC}=\dfrac{\dfrac{1}{3}BC}{BC}\\\\&\Leftrightarrow&\dfrac{CN}{AC}=\dfrac{BC}{3\times BC}\\\\&\Leftrightarrow&\dfrac{CN}{AC}=\dfrac{1}{3}\end{array}$

 

D'où, $\boxed{\dfrac{CN}{AC}=\dfrac{1}{3}}$

 

b) Calculons $NC.$

 

D'après le résultat de la question $a)$, on a : $\dfrac{CN}{AC}=\dfrac{1}{3}.$

 

Ce qui donne alors :

$$CN=\dfrac{1}{3}AC$$

Ainsi, en remplaçant $AC$ par sa valeur, on trouve :

 

$CN=\dfrac{1}{3}\times 9=\dfrac{9}{3}=3$

 

D'où, $\boxed{NC=3\;cm}$

 

4) Calculons $MN.$

 

En effet, comme les triangles $ABC\ $ et $\ CMN$ sont en position de Thalès alors, le coefficient $k$ de réduction des longueurs est :

$$k=\dfrac{CN}{AC}=\dfrac{1}{3}$$

Donc, pour trouver la longueur d'un côté du triangle $CMN$, on multiplie par $\dfrac{1}{3}$ la longueur du côté correspondant du triangle $ABC.$

 

Ainsi, $MN=\dfrac{1}{3}AB=\dfrac{6}{3}=2$

 

D'où, $\boxed{MN=2\;cm}$

 

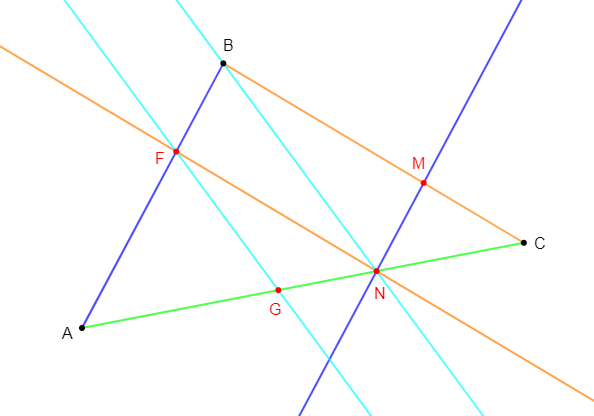
5) La parallèle à $(BC)$ passant par $N$ coupe $(AB)$ en $F.$

 

La parallèle à $(BN)$ passant par $F$ coupe $(AC)$ en $G.$

 

Démontrons que : $AN^{2}=AC\times AG.$

 

En effet, les droites $(BC)\ $ et $\ (FN)$ étant parallèles alors, les triangles $ABC\ $ et $\ AFN$ sont en position de Thalès.

 

Donc, en appliquant le théorème de Thalès, on a :

$$\dfrac{AN}{AC}=\dfrac{AF}{AB}\quad(1)$$

De la même manière, les droites $(BN)\ $ et $\ (FG)$ étant parallèles alors, les triangles $ABN\ $ et $\ AFG$ sont en position de Thalès.

 

Ainsi, d'après le théorème de Thalès, on a :

$$\dfrac{AG}{AN}=\dfrac{AF}{AB}\quad(2)$$

En comparant les égalités $(1)\ $ et $\ (2)$, on peut alors écrire :

$$\dfrac{AN}{AC}=\dfrac{AG}{AN}$$

Par suite,

 

$\begin{array}{rcl}\dfrac{AN}{AC}=\dfrac{AG}{AN}&\Leftrightarrow&AN\times AN=AC\times AG\\\\&\Leftrightarrow&AN^{2}=AC\times AG\end{array}$

 

D'où, $\boxed{AN^{2}=AC\times AG}$