Série N°9 : Statistiques 1er - L

La méthode de Mayer consiste à partager un nuage de points dans $14$ ordre croissant de leurs abscisses en deux sous groupes de même effectifs.

 

Chacun des deux sous-groupes est alors remplacé par le point dont les coordonnées sont respectivement :

 

$-\ $En abscisse, la moyenne arithmétique des abscisses des points du sous-groupe.

 

$-\ $En ordonnée, la moyenne arithmétique des ordonnées des points du sous-groupe

 

 

 

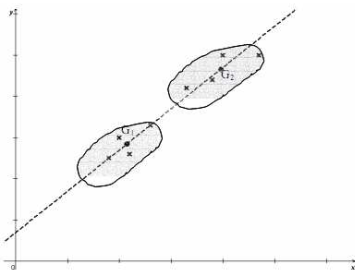
Par ces points que l'on nomme $G1$ et $G2$ passe une seule droite qui sera la droite d'ajustement.

 

On détermine l'équation de la droite à partir des coordonnées de ces deux points :

 

$\right. G_{1}\ :\ y_{1}=ax_{1}+b\\ G_{2}\ :\ y_{2}ax_{2}+b\left\rbrace\begin{array}{rcl}$

 

$a$ et $b$ sont les inconnues que l'on cherche.

 

$x_{1}$ et $y_{1}$ sont les coordonnées du premier point $G_{1}.$

 

$x_{2}$ et $y_{2}$ sont les coordonnées du deuxième point $G_{2}.$

 

$x_{2}$ et $y_{2}$ sont les coordonnées du deuxième point $G_{2}$

 

Le tableau ci-dessous donne l'évolution du prix de la tartelette aux framboises dans une pâtisserie.

$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Année }&2004&2005&2006&2007&2008&2009\\ \hline \text{Rang de l'année }x_{i}&1&2&3&4&5&6\\ \hline \text{Nombre d'accident }y_{i}&1.75&2&2.1&2.25&2.4&2.55\\ \hline \end{array}$$

 

1. Représenter cette série statistique dans un repère orthonormé (unités $1\,cm$ pour $1$ unité en abscisse et $2\,cm$ pour une unité en ordonnée). 

 

Peut-on envisager un ajustement affine ?

 

2. Trace à main levée la droite d'ajustement.

Le tableau suivant indique, pour chaque année, le nombre d'accidents causés par les automobilistes sur la circulation.

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline \text{Année }&1997&1998&1999&2000&2001&2002&2003\\ \hline \text{Rang de l'année }x_{i}&0&1&2&3&4&5&6\\ \hline \text{Nombre d'accident }y_{i}&266&281&312&334&355&374&395\\ \hline \end{array}$$

 

1. Construire le nuage des points associés à cette série statistique $\left(x_{i}\;,y_{i}\right)$

 

2. Trace à main levée la droite de régression.

Un fermier doit embaucher des ouvriers agricoles.

 

Lors de précédents recrutements analogues, il a fallu une étude statistique et a dressé le tableau suivant.

$$\begin{array}{|c|c|c|c|c|} \hline \text{Salaires proposés en }FCFA\left(x_{i}\right)&60000&64000&68000&72000\\ \hline \text{Nombre de candidatures }\left(y_{i}\right)&11&17&20&25\\ \hline \end{array}$$

 

1. Construire le nuage des points associés à cette série statistique $\left(x_{i}\;,y_{i}\right)$

 

2. Méthode de la droite de Mayer :

 

a. On appelle $G_{1}$ le point moyen des deux premiers relevés et $G_{2}$ le point moyen des deux derniers relevés.

 

Calcule les coordonnées de $G_{1}$ et de $G_{2}$

 

b. Donner l'équation de la droite de $\left(G_{1}G_{2}\right)$