Bac Maths D, Tunisie 2019
Exercice 1
Les individus âgés de plus de $60$ ans représentent $30\%$ de la population de cette ville.
On choisit, au hasard, une personne de cette population et on considère les évènements suivants :
$\bullet\ G$ : « La personne est âgés de plus de $60$ ans ».
$\bullet\ V$ : « La personne est vaccinée ».
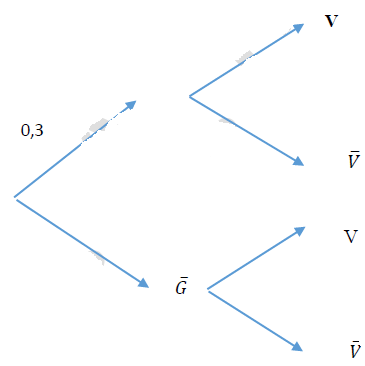
1. Recopier et compléter l'arbre de probabilité ci-dessous.
2. Montrer que la probabilité pour qu'une personne soit vaccinée est égale à $0.345.$
3. La personne choisie étant vaccinée, quelle est la probabilité pour qu'elle soit âgée de moins de $60$ ans.
4. On choisit au hasard $10$ personnes âgées de plus de $60$ ans.
Calculer la probabilité pour que deux exactement d'entre elles soient vaccinées.
5. On choisit, au hasard, $n$ personnes âgées de plus de $60$ ans.
a) Quelle est la probabilité pour qu'aucune d'entre elles ne soit vaccinée ?
b) Déterminer la probabilité $p_{n}$ pour que l'une au moins d'entre elle soit vaccinée.
c) Déterminer la plus petite valeur de $n$ pour que $p_ {n}\geq 0.9.$
Exercice 2
a) Montrer que $a=2\mathrm{e}^{\mathrm{\dfrac{5\pi}{12}}}.$
b) Donner les valeurs exactes de $\cos\left(\dfrac{11\pi}{12}\right)$ et $\sin\left(\dfrac{11\pi}{12}\right).$
2. a) Vérifier que $a^{4}=8(1-\mathrm{i}\sqrt{3}).$
b) En déduire les solutions de l'équation $(E)\ :\ z^{4}=8(1-\mathrm{i}\sqrt{3}).$
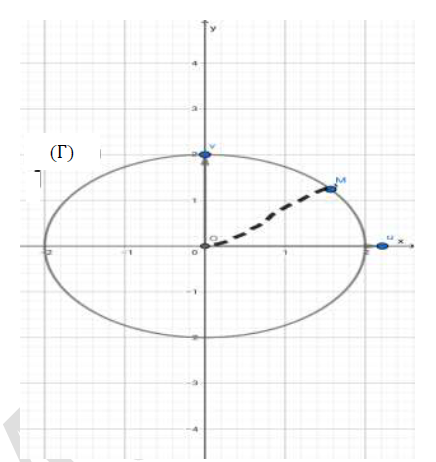
c) Dana la figure 1 de l'annexe jointe, le plan est muni d'un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v}).$
$\Gamma$ est le cercle trigonométrique et $H$ est le point d'affixe $\mathrm{e}^{\mathrm{i}\dfrac{\pi}{12}}.$
Placer les images des solutions de l'équation $(E).$
Exercice 3
$$\left\lbrace\begin{array}{lcl} x&=&\alpha\\ y&=&\alpha\quad;\quad\alpha\in\mathbb{N}\\ z&=&−\alpha+2 \end{array}\right.$$
1. a) Montrer que les points $A$, $B$ et $C$ définissent un plan $\mathcal{P}.$
b) Montrer qu'une équation $\mathcal{P}$ est $x+y+z+2=0.$
2. Soit le point $E(2\ ;\ 2\ ;\ 0)$
a) Vérifier que $E$ n'appartient pas à $\mathcal{P}.$
b) Calculer le volume du tétraèdre $EABC.$
3. Montrer que la droite $\Delta$ est perpendiculaire au plan $\mathcal{P}$ en un point que l'on précisera.
4. Soit $\alpha\neq 0$ et $M(\alpha\ ;\ \alpha\ ;\ -\alpha+2)$ un point de $\Delta.$
a) Calculer en fonction de $\alpha$ le volume du tétraèdre $MABC.$
b) En déduire les coordonnées des points $M$ pour lesquels le volume du tétraèdre $MABC$ est égale au double du volume du tétraèdre $EABC.$
Exercice 4
1. a) Montrer que $f$ est dérivable sur $I$ et que $f'(x)=\dfrac{1}{2(x+\sqrt{x})}.$
b) Montrer que $\lim\limits_{\to 0^{+}}\dfrac{f(x)}{x}=+\infty.$ Interpréter graphiquement ce résultat.
c) Calculer $\lim\limits_{x\to +\infty}f(x)$ et $\lim\limits_{x\to +\infty}\dfrac{f(x)}{x}.$ Interpréter graphiquement les résultats.
d) Dresser le tableau de variation de $f.$
e) Montrer que $f$ réalise une bijection de $I$ vers $I.$
f) On désigne par $f^{-1}$ la fonction réciproque de $f.$
Montrer que pour tout $x\geq 0\;,\ f^{−1}(x)=(\mathrm{e}^{x}-1)^{2}.$
2. Soit $J=\left[\dfrac{1}{4}\ ;\ 1\right]$
a) Montrer que pour tout $x\in J \;,\ f'(x)\leq\dfrac{2}{3}.$
b) Montrer que l'équation $f(x)=x$ admet dans l'intervalle $J$ une unique solution $\alpha$ vérifiant $0.5<\alpha<0.6.$
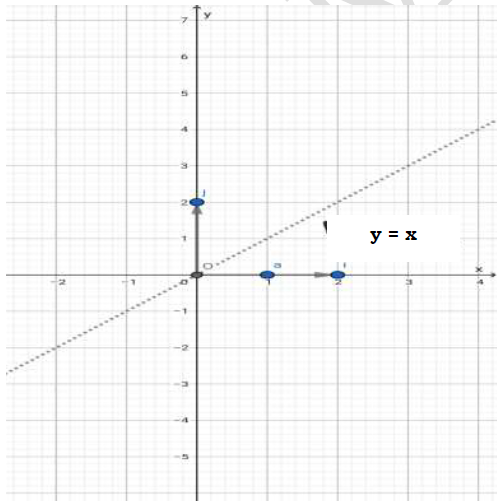
3. Dans la figure 2 de l'annexe jointe, on a représenté dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ le réel $\alpha$ et la droite $\Delta$ d'équation $y=x.$
a) Tracer dans la figure 2 les courbes $\mathcal{C_{f}}$ et $\mathcal{C_{f}^{-1}}$ Désigne la courbe représentative de la fonction $f^{-1}.$
(On précisera les demi-tangentes).
b) Calculer, en fonction de $\alpha$, l'aire de la partie du plan limitée par $\mathcal{C_{f}}$, $\mathcal{C_{f}^{-1}}$ et les droites d'équations respectives $x=0$ et $x=\alpha.$
4. On considère la suite $\left(u_{n}\right)n\in\mathbb{N}$ définie par :
$$\left\lbrace\begin{array}{lcl} u_{0}&=&1\\ u_{n+1}&=&f\left(u_{n}\right) \end{array}\right.$$
a) Montrer que pour tout entier naturel $n$, $u_{n}\in\left[\dfrac{1}{4}\ ;\ 1\right].$
b) Montrer que pour tout entier naturel $n$, $\left|u_{n}-\alpha\right|\leq \left(\dfrac{2}{3}\right)^{n}.$
c) En déduire que la suite $\left(u_{n}\right)$ est convergente et donner sa limite.
d) Soit la suite $\left(v_{n}\right)n\in\mathbb{N}$ définie par $v_{n}=f^{−1}\left(u_{n}\right).$
Montrer que la suite $\left(v_{n}\right)$ est convergente et déterminer sa limite.
Annexe (à rendre avec la copie)

Ajouter un commentaire