Solution des exercices : Rotations et polygones réguliers - 4e

 

1) Définissons un angle au centre.

 

On appelle angle au centre, un angle dont le sommet est le centre d'un cercle.

 

2) En utilisant la figure ci-dessous ; nommons les angles au centre.

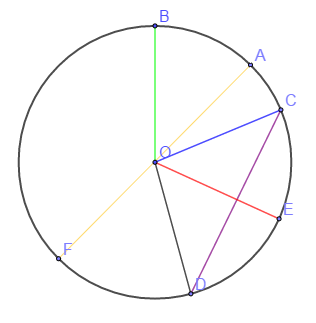
Nous observons les angles au centre suivants :

 

$\widehat{OFD}\;,\ \widehat{OFE}\;,\ \widehat{OFC}\;,\ \widehat{OFA}\;,\ \widehat{OFB}$

 

$\widehat{ODE}\;,\ \widehat{ODC}\;,\ \widehat{ODA}\;,\ \widehat{ODB}\;,\ \widehat{OEC}$

 

$\widehat{OEA}\;,\ \widehat{OEB}\;,\ \widehat{OCA}\;,\ \widehat{OCB}\;,\ \widehat{OAB}$

Soit $\mathcal{C}$ un cercle de centre $O$ et de rayon $3\;cm.\ \widehat{ENS}$ est un angle au centre. Complétons le tableau suivant : On donne $\pi=3.$

$$\begin{array}{|lcccc|}\hline mes\widehat{ENS}& {30}^{\circ }& & {126}^{\circ }& \\ \text{Longueur de l'arc}& & & & \\ \text{intercepté par}& & {\displaystyle \frac{2\pi }{3}}& & {\displaystyle \frac{\pi }{3}}\\ \widehat{ENS}\text{ en }cm& & & & \\ \hline\end{array}$$

Pour compléter le tableau, on procède comme suit :

 

En effet, comme $\widehat{ENS}$ est un angle au centre alors, son sommet $N$ est confondu au point $O$ centre du cercle $\mathcal{C}.$

 

Soit : $\ell$ la longueur de l'arc intercepté par l'angle $\widehat{ENS}$

 

Alors, on a :

$$\ell =r\times mes\widehat{ENS}\text{et donc,}mes\widehat{ENS}={\displaystyle \frac{\ell }{r}}$$

avec $r=3\;cm$ rayon du cercle $\mathcal{C}\ $ et $\ mes\,\widehat{ENS}$ en radian.

 

Soit la correspondance suivante :

$$\begin{array}{rcl}{180}^{\circ }& ⟶& \pi rad\\ \\ {\alpha }^{\circ }& ⟶& xrad\end{array}$$

En appliquant la propriété de proportionnalité, on obtient :

$${\displaystyle \frac{x}{\pi }}={\displaystyle \frac{\alpha }{180}}$$

Par suite,

 

$$x={\displaystyle \frac{\alpha \times \pi }{180}}rad$$

 

Ainsi,

 

$-\ $ pour $\alpha=30^{\circ}$, on trouve :

 

$$$\begin{array}{rcl}x& =& {\displaystyle \frac{30\times \pi }{180}}\\ \\ & =& {\displaystyle \frac{\pi }{6}}\end{array}$$$

 

D'où, $\ell=3\times\dfrac{\pi}{6}=\dfrac{\pi}{2}$

 

$-\ $ pour $\alpha=126^{\circ}$, on obtient :

 

$$$\begin{array}{rcl}x& =& {\displaystyle \frac{126\times \pi }{180}}\\ \\ & =& {\displaystyle \frac{7\pi }{10}}\end{array}$$$

 

Ce qui donne, $\ell=3\times\dfrac{7\pi}{10}=\dfrac{21\pi}{10}$

 

Par ailleurs,

 

$-\ $ Si $\ell=\dfrac{\pi}{3}$ alors,

 

$$$\begin{array}{rcl}mes\widehat{ENS}& =& {\displaystyle \frac{{\displaystyle \frac{\pi }{3}}}{3}}\\ \\ & =& {\displaystyle \frac{\pi }{9}}\\ \\ & =& {20}^{\circ }\end{array}$$$

 

$-\ $ Si $\ell=\dfrac{2\pi}{3}$ alors,

 

$$$\begin{array}{rcl}mes\widehat{ENS}& =& {\displaystyle \frac{{\displaystyle \frac{2\pi }{3}}}{3}}\\ \\ & =& {\displaystyle \frac{2\pi }{9}}\\ \\ & =& {40}^{\circ }\end{array}$$$

 

On obtient alors le tableau suivant :

$$\begin{array}{|lcccc|}\hline mes\widehat{ENS}& {30}^{\circ }& {40}^{\circ }& {126}^{\circ }& {20}^{\circ }\\ \text{Longueur de l'arc}& & & & \\ \text{intercepté par}& 1.5& 2& 6.3& 1\\ \widehat{ENS}\text{ en }cm& & & & \\ \hline\end{array}$$

Soient $[MN]\ $ et $\ [M'N']$ deux segments de même longueur dont les supports ne sont pas parallèles.

 

1) Faisons une figure.

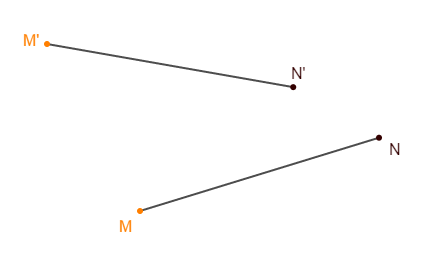
2) Par une certaine rotation, l'image de $M$ est $M'$ et l'image de $N$ est $N'.$

 

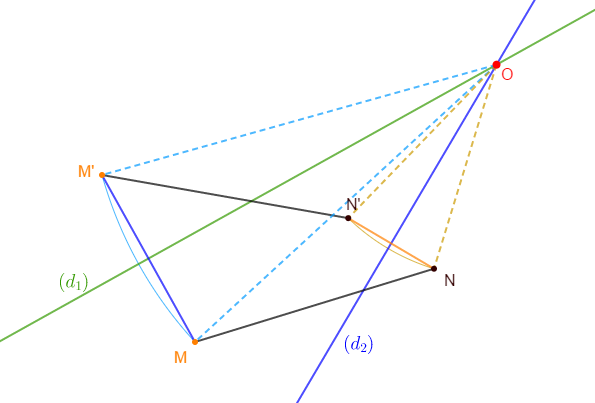
3) Construisons le centre $O$ de cette rotation.

 

En effet, soit $(d_{1})$ la médiatrice du segment $[MM']$ alors, tout point de $(d_{1})$ est équidistant des points $M\ $ et $\ M'.$

 

Par suite, le centre $O$ de la rotation qui transforme $M$ en $M'$ appartient à $(d_{1}).$

 

De la même manière, soit $(d_{2})$ la médiatrice du segment $[NN']$ alors, le centre $O$ de la rotation qui transforme $N$ en $N'$ appartient à $(d_{2}).$

 

Par conséquent, le centre $O$ de cette rotation est le point de rencontre des médiatrices $(d_{1})\ $ et $\ (d_{2})$ des segments $[MM']\ $ et $\ [NN']$ respectivement.