Géométrie dans l'espace - 1er S
Classe:
Première
L'espace $\mathcal{E}$ est un ensemble infini dont les éléments sont appelés points.
Les droites et les plans sont des parties infinies propres de l'espace, c'est-à-dire des parties de l'espace distinctes de celui-ci.
I. Axiome de la géométrie dans l'espace
Axiome 0 :
Toutes les règles de la géométrie plane restent valables dans chaque plan de l'espace.
Axiome 1 :
Par deux points distincts de $\mathcal{E}$, il passe une droite et une seule.
La notation $(AB)$ désignera la droite contenant ces deux points.
Axiome 2 :
Il existe un plan et un seul contenant trois points non alignés.
Axiome 3 :
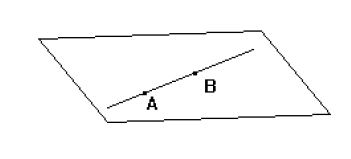
Une droite qui a deux points dans un plan y est contenue toute entière.
$$(A\in\mathcal{P}\;,\ B\in\mathcal{P})\Longrightarrow((AB)=D\subset\mathcal{P}).$$
Axiome 4 :
Tout plan $\mathcal{P}$ divise l'espace $\mathcal{E}$ en deux régions disjointes (sans point commun) ; ces deux régions $\mathcal{E}_{1}$ et $\mathcal{E}_{2}$ sont appelées demi-espaces.
$-\ \ $ Si $A$ et $B$ appartiennent à un même demi-espace, tout le segment $[AB]$ est inclus dans ce demi-espace.
(On parle de convexité du demi-espace).
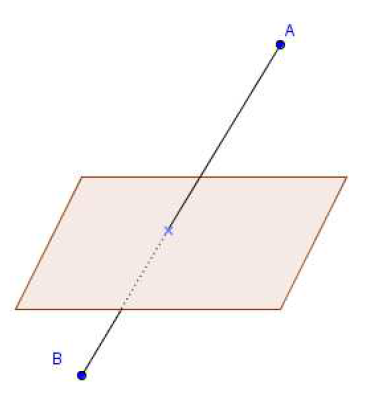
$-\ \ $ Si $A$ et $B$ sont de part et d'autre de $\mathcal{P}$, alors $[AB]$ a un point dans $\mathcal{P}$ et un seul.
II. Propriétés d'incidence
1) Position relative d'une droite et d'un plan
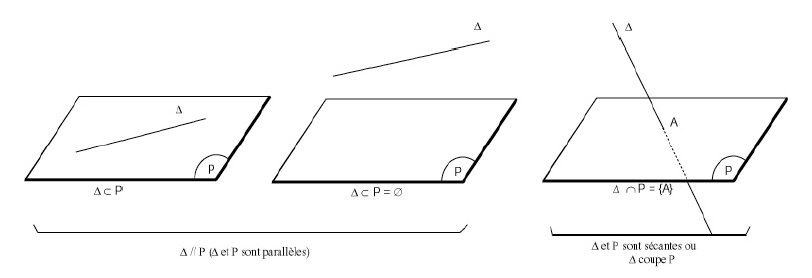
Une droite $\Delta$ peut avoir :
$-\ \ $ 0 (c'est-à-dire aucun) point dans un plan $\mathcal{P}$ : elle est alors dite parallèle au plan.
$-\ \ $ un seul point commun avec un plan : on dit que $D$ coupe $\mathcal{P}$ ou que $\Delta$ est sécante avec $\mathcal{P}.$
$-\ \ $ au moins deux points communs avec un plan $\mathcal{P}$ : elle est alors incluse dans $\mathcal{P}$ d'après l'Axiome 3.
N.B.
Dans ce dernier cas, on dit aussi que $\Delta$ est parallèle à $\mathcal{P}.$
2) Détermination d'un plan
En vertu de l'Axiome 2, il existe un plan unique contenant une droite $\mathcal{D}$ et un point $A$ extérieur à $\mathcal{D}.$
(En effet, il suffit de choisir $2$ points distincts de $\mathcal{D}.$
Avec le point $A$, on obtient alors $3$ points non alignés).
On dit que la droite $\mathcal{D}$ et le point $A$ déterminent un plan.
De même, un plan est déterminé par deux droites sécantes.
(En effet, il suffit de prendre leur point point d'intersection et deux points $A$ et $B$ appartenant respectivement aux deux droites).
3) Intersection de deux plans
Théorème 1 :
Si deux plans distincts ont (au moins) un point commun $O$, alors leur intersection est une droite.
Démonstration :
Soient $\Delta_{1}$ et $\Delta_{2}$ deux droites sécantes en $O$ situées dans le plan $\mathcal{P}$ et non dans le plan $\mathcal{Q}.$
$\mathcal{P}$ divise l'espace en $2$ régions $\mathcal{E}_{1}$ et $\mathcal{E}_{2}$ (Axiome 4).
Alors, nécessairement $\Delta_{1}\cap\mathcal{E}_{1}\neq\varnothing$, car sinon, comme $\Delta_{1}$ n'est pas située dans $\mathcal{Q}$, $\Delta_{1}$ serait incluse dans $\mathcal{E}_{2}$, ce qui est impossible, puisque $\Delta_{1}$ passe par le point $O$ de $\mathcal{Q}.$
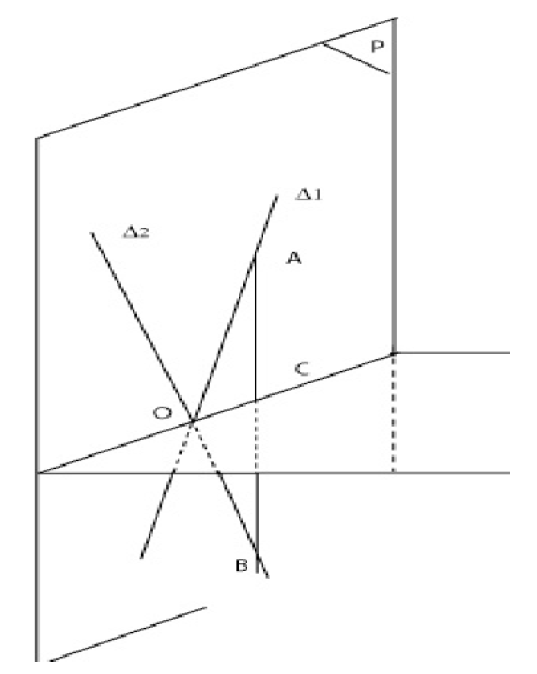
De même : $\Delta_{1}\cap\mathcal{E}_{2}\neq\varnothing$, $\Delta_{2}\cap\mathcal{E}_{1}\neq\varnothing$, $\Delta_{2}\cap\mathcal{E}_{2}\neq\varnothing.$
Soit $A$ un point de $\Delta_{1}\cap\mathcal{E}_{1}$ et $B$ un point de $\Delta_{2}\cap\mathcal{E}_{2}.$
Daprès l'Axiome 4, $(AB)$ a un point commun unique $C$ avec le plan $\mathcal{P}.$
Nécessairement, $C$ et $O$ sont distincts, sans quoi $\Delta_{1}$ et $\Delta_{2}$ seraient confondues.
$\mathcal{P}$ et $\mathcal{Q}$ ont donc en commun la droite $(CO)$ et ne peuvent avoir en commun un autre point $M$ en dehors de $(CO)$ sinon ils seraient confondus.
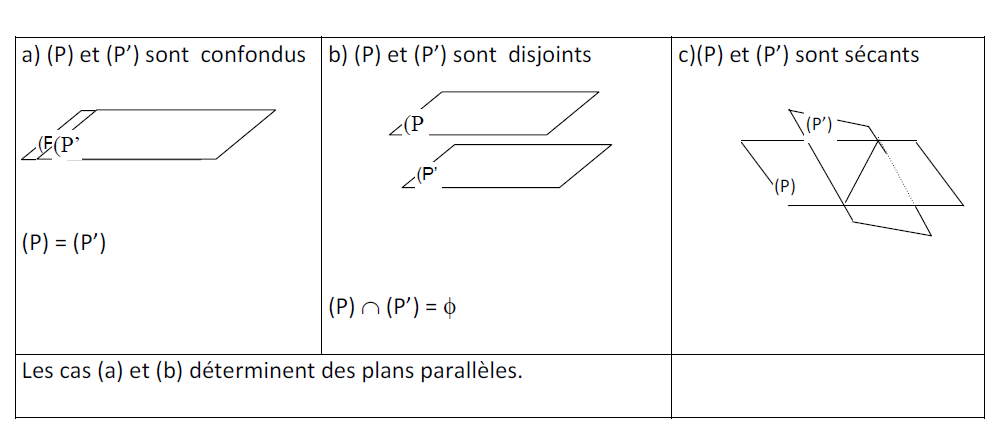
4) Positions relatives de deux plans
D'après le théorème précédent, deux plans $\mathcal{P}$ et $\mathcal{Q}$ peuvent être :
$-\ \ $ sans point commun ; on dit qu'ils sont parallèles ;
$-\ \ $ sécants suivant une droite ;
$-\ \ $ confondus.
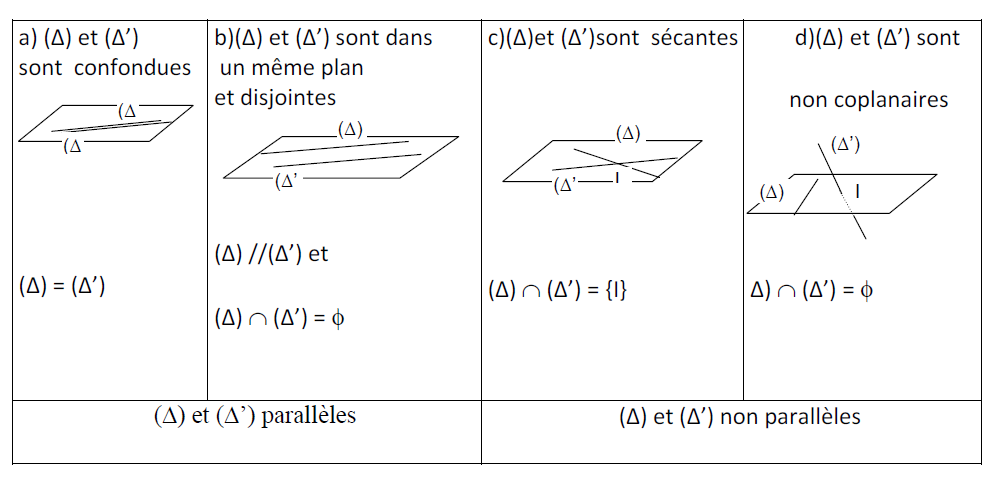
5) Positions relatives de deux droites
Soient $\mathcal{D}$ et $\Delta$ deux droites ;
$-\ \ $ Si elles sont sécantes, elles sont coplanaires d'après 2)
$-\ \ $ Si elles n'ont pas de point commun, soit $\mathcal{P}$ le plan déterminé par $\mathcal{D}$ et un point arbitraire $A$ de $\Delta.$
$\bullet$ Si $\mathcal{P}$ contient $\Delta$, alors $\mathcal{D}$ et $\Delta$ sont deux droites de $\mathcal{P}$ qui n'ont aucun point commun :
Elles sont parallèles
$\bullet$ Si $\mathcal{P}$ coupe $\Delta$, $\mathcal{D}$ et $\Delta$ ne sont pas dans un même plan, sans quoi ce plan contiendrait $\mathcal{D}$ et $\Delta$ et serait confondu avec le plan $\mathcal{P}.$
$\Delta$ serait incluse dans $\mathcal{P}$ : contradiction.
On dit que $\mathcal{D}$ et $\Delta$ sont non coplanaires.
En résumé :
Deux droites de l'espace peuvent être :
$-\ \ $ coplanaires : elles sont alors soit sécantes, soit parallèles.
$-\ \ $ non coplanaires : c'est le cas général
N.B.
Dans le plan, quand deux droites ne sont pas sécantes, elles sont alors parallèles (distinctes ou confondues).
Dans l'espace, il en va différemment.
$\bullet$ Dire que deux droites sont sécantes signifie qu'elles n'ont qu'un seul point en commun.
$\bullet$ Dire que deux droites sont parallèles signifie qu'elles sont coplanaires et ne sont pas sécantes.
6) Positions relatives de quatre points
Quatre points de l'espace ne sont généralement pas coplanaires.
Ils limitent $4$ triangles situés dans quatre plans différents.
Le solide ainsi constitué est appelé tétraèdre.
III. Parallélisme de deux droites
On rappelle que deux droites de l'espace sont parallèles si et seulement si :
a) Elles n'ont pas de point commun ;
b) Elles sont coplanaires.
Théorème 2 :
Par un point extérieur à une droite, il passe une parallèle et une seule à cette droite.
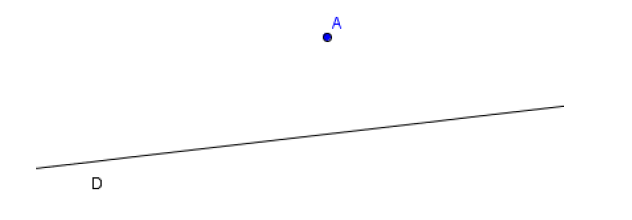
Démonstration :
En effet, il existe un plan unique contenant $A$ et $\mathcal{D}.$
Toute parallèle à $\mathcal{D}$ passant par $A$ est nécessairement située dans le plan $(\mathcal{D}\;,\ A).$
Or, d'après la géométrie plane (cf. Axiome 0), il existe dans le plan $(\mathcal{D}\;,\ A)$ une seule droite passant par $A$ et parallèle à $\mathcal{D}.$
Théorème 3
Si $(\Delta)$ et $(\Delta')$ sont deux droites parallèles, alors tout plan qui coupe $(\Delta)$ coupe aussi $(\Delta').$
Démonstration :
Soit $(\Pi)$ le plan formé par $(\Delta)$ et $(\Delta').$
Supposons un plan $(\mathcal{P})$ sécant à $(\Delta).$
Alors la droite $(\mathcal{D})$, intersection de $(\Pi)$ et $(\mathcal{P})$, est sécante à $(\Delta)$, donc elle est aussi sécante à $(\Delta')$ dans le plan $(\Pi).$
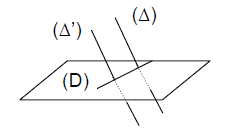
Si $(\mathcal{P})$ n'était pas sécante à $(\Delta')$ , $(\mathcal{P})$ contiendrait $(\Delta')$ et un point de $(\Delta)$ donc contiendrait ces deux droites parallèles.
Ce qui est contraire à l'hypothèse $(\mathcal{P})$ sécant à $(\Delta).$
D'où $(\mathcal{P})$ est sécante à $(\Delta').$
Théorème 4 :
Lorsque deux droites sont parallèles, tout plan qui coupe l'une coupe l'autre.
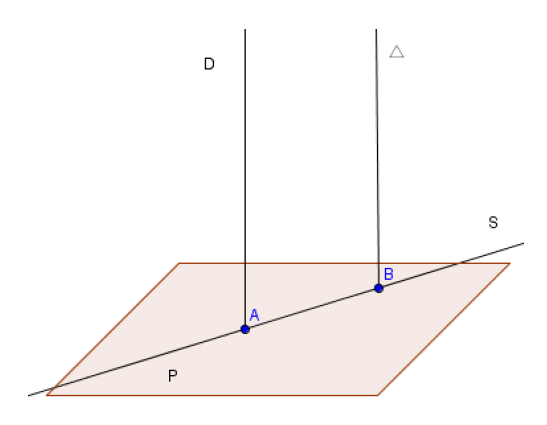
Démonstration :
On a $\mathcal{D}\parallel\Delta$ et $\mathcal{P}\cap\Delta={A}.$
$\mathcal{D}$ et $\Delta$ déterminent un plan $\pi$ qui coupe $\mathcal{P}$ suivant une droite $S.$
$S$ est une droite du plan $\pi$ qui coupe $\mathcal{D}$ en $A$, donc elle coupe sa parallèle $\Delta$ (d'après la géométrie plane) en un point $B.$
Donc $\mathcal{P}$ coupe $\Delta$ en $B.$
Théorème 5 :
Deux droites distinctes parallèles à une même troisième sont parallèles entre elles.
Si $(\Delta)\parallel (\Delta')$ et $(\Delta')\parallel (\Delta'')$ alors $(\Delta)\parallel (\Delta'')$
Démonstration :
Supposons que $(\Delta)$ non parallèle à $(\Delta'').$
On a :
Soit $(\Delta)\cap(\Delta'')={I}$, soit $(\Delta)$ et $(\Delta'')$ non coplanaires
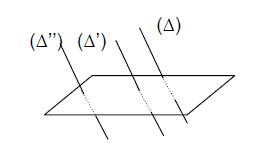
$\bullet$ Si $(\Delta)\cap(\Delta'')={I}.$
Par $I$, passeraient deux parallèles à $(\Delta')$, ce qui contredit le théorème 2.
Donc $(\Delta)$ et $(\Delta'')$ ne sont pas sécantes.
Si $(\Delta)$ et $(\Delta'')$ sont non coplanaires, il existe un plan $(\mathcal{P})$ qui contient $(\Delta'')$ et qui coupe $(\Delta)$ donc $(\mathcal{P})$ coupe $(\Delta')$ d'après le théorème 2 donc $(\Delta')$ et $(\Delta'')$ sont non coplanaires.
Ce qui est contradictoire car deux droites parallèles sont coplanaires.
Donc $(\Delta)\parallel (\Delta'').$
IV. Parallélisme d'une droite et d'un plan
Rappelons qu'une droite $\mathcal{D}$ et un plan $\mathcal{P}$ sont dits parallèles s'ils n'ont aucun point commun
$$\left(\text{i.e}\mathcal{D}\cap\mathcal{P}=\varnothing\right)$$
Théorème 6 :
Une droite $\mathcal{D}$ est parallèle à un plan $\mathcal{P}$ si et seulement si $\mathcal{D}$ est parallèle à une droite de $\mathcal{P}.$
En d'autres termes :
$$\underbrace{\left(\mathcal{D}\parallel\mathcal{P}\right)}_{(\text{i})}\Leftrightarrow\underbrace{\left(\text{Il existe une droite }\Delta\text{ de }\mathcal{P}\text{ telle que }\mathcal{D}\parallel\Delta\right)}_{(\text{ii})}$$
Démonstration :
$\bullet$ Montrons que (i)$\Longrightarrow$(ii) :
Supposons que $\mathcal{D}\parallel\mathcal{P}$ et soit $O$ un point quelconque de $\mathcal{P}.$
Le plan $(\mathcal{D}\;,\ O)$ coupe $\mathcal{P}$ suivant une droite $\Delta$ qui est nécessairement parallèle à $\mathcal{D}$
$\bullet$ Montrons que (ii)$\Longrightarrow$(i) :
Supposons que $\mathcal{D}$ soit parallèle à une droite $\Delta$ de $\mathcal{P}$ et que $\mathcal{D}$ ne soit pas incluse dans $\mathcal{P}.$
Alors $\mathcal{P}$ ne coupe pas $\mathcal{D}$ car s'il coupait $\mathcal{D}$, il couperait $\Delta$ (cf. théorème 3).
Or, par hypothèse $\mathcal{D}\cup\mathcal{P}.$
D'où $\mathcal{P}\parallel\Delta.$
Conséquence 1 :
Si $\mathcal{D}\parallel\mathcal{P}$, la parallèle menée par un point $A$ de $\mathcal{P}$ à $\mathcal{D}$ est incluse dans $\mathcal{P}.$
Démonstration :
En effet, le plan $(\mathcal{D}\;,\ A)$ coupe $\mathcal{P}$ suivant une droite $\Delta$ parallèle à $\mathcal{D}.$
$\Delta$ est la parallèle unique à $\Delta$ passant par $A.$
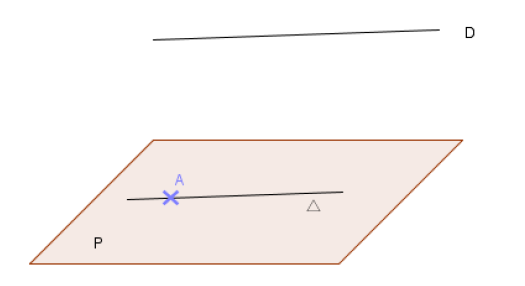
Conséquence 2 : (Théorème du toit) :
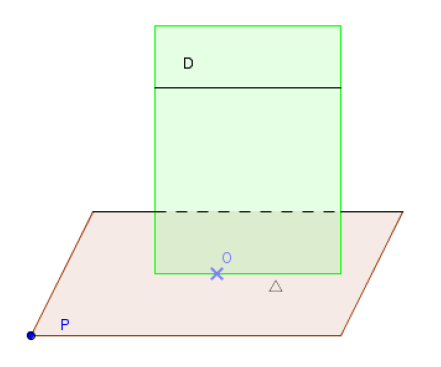
Si une droite est parallèle à deux plans sécants, alors elle est parallèle à leur intersection.
$$\left(\mathcal{P}\cap\mathcal{Q}=\Delta\;;\ \mathcal{D}\parallel\mathcal{P}\text{ et }\mathcal{D}\parallel\mathcal{Q}\right)\Longrightarrow\left(\mathcal{D}\parallel\Delta\right).$$
Démonstration :
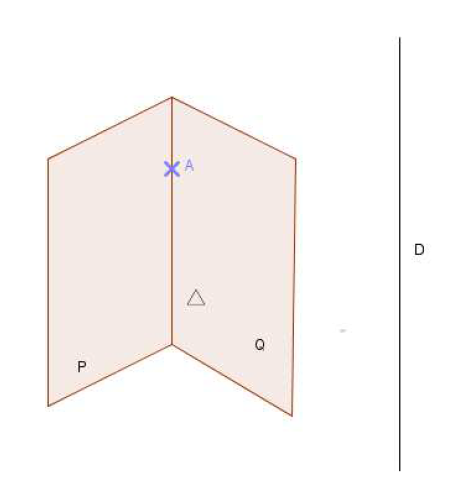
Soit $A\in\mathcal{P}\cap\mathcal{Q}.$
La parallèle menée par $A$ à $\mathcal{D}$ est incluse dans $\mathcal{P}$ et dans $\mathcal{Q}$ d'après la conséquence 1.
Elle est donc confondue avec $\Delta.$
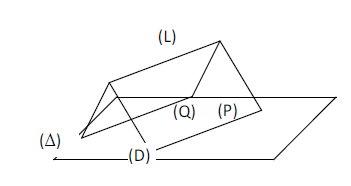
En particulier, dans la configuration ci-dessous, la droite d'intersection $(L)$ de $(\mathcal{P})$ et $(\mathcal{Q})$ est parallèle à la fois à $(\mathcal{D})$ et $(\Delta).$
V.Parallélisme de plans
Rappel (cf. 2.4) :
Deux plans parallèles sont deux plans qui sont confondus ou bien qui n'ont aucun point commun.
Remarque :
Si deux plans distincts sont parallèles, alors toute droite de l'un des plans est parallèle à l'autre plan.
Théorème 7 :
Deux plans distincts $\mathcal{P}$ et $\mathcal{Q}$ sont parallèles si et seulement si deux droite distinctes de l'une sont parallèles à l'autre.
$$\underbrace{\left(\mathcal{P}\neq\mathcal{Q}\text{ et }\mathcal{P}\parallel\mathcal{Q}\right)}_{(\text{i})}\Leftrightarrow\underbrace{\left(\text{Il existe deux droites }\mathcal{D}\text{ et }\Delta\text{ de }\mathcal{P}\text{ sécantes en }O\text{ telles que }\mathcal{D}\parallel\mathcal{Q}\text{ et }\Delta\parallel\mathcal{Q}\right)}_{(\text{ii})}$$
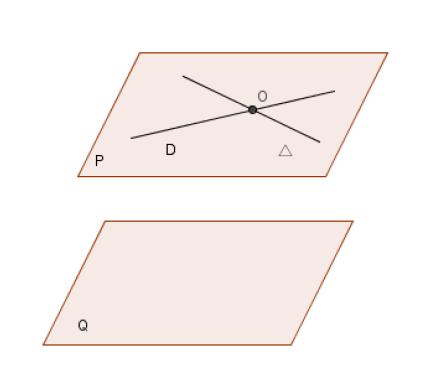
(i)$\ \Rightarrow\ $(ii) : Évident car toute droite de $\mathcal{P}$ est parallèle à $\mathcal{Q}$ (cf. remarque précédant le théorème 6).
(ii)$\ \Rightarrow\ $(i) : Si $\mathcal{P}$ coupait $\mathcal{Q}$ suivant une droite $\mathcal{S}$, $\mathcal{D}$ serait parallèle à $\mathcal{S}$ ainsi que $\Delta.$
Par le point $O$, passeraient deux parallèles $\mathcal{D}$ et $\Delta$ à $\mathcal{S}$ : absurde.
Donc $\mathcal{P}$ est parallèle à $\mathcal{Q}.$
Théorème 8 :
Par un point $O$ donné de l'espace, extérieur à un plan $\mathcal{P}$, il passe un plan $\mathcal{P}_{0}$ et un seul parallèle à $\mathcal{P}.$
Démonstration :
a) Existence :
Considérons deux droites $\mathcal{D}$ et $\Delta$ de $\mathcal{P}$ sécantes en $A.$
Soit $\mathcal{D'}$ la parallèle à $\mathcal{D}$ passant par $O$ et $\Delta'$ la parallèle à $\Delta$ passant par $O.$

$\mathcal{D'}$ étant parallèle à la droite $\mathcal{D}$ du plan $\mathcal{P}$ est parallèle à $\mathcal{P}$ (théorème 5).
De même $\Delta'\parallel\mathcal{P}.$
Le plan $(\mathcal{D'}\;,\ \Delta')$ est alors parallèle à $\mathcal{P}$ d'après le théorème 6.
b) Unicité :
Supposons qu'il existe un autre plan $\mathcal{Q}$ passant par $O$ et parallèle à $\mathcal{P}.$
$\mathcal{Q}$ n'est parallèle (au sens strict) au plan $(\mathcal{D'}\;,\ \Delta')$ car $\mathcal{Q}$ passe par $O\in(\mathcal{D'}\;,\ \Delta').$
Si $\mathcal{Q}$ coupait $\mathcal{D'}$, il couperait aussi sa parallèle $\mathcal{D}$ (théorème 3), ce qui est absurde puisque $\mathcal{Q}\parallel\mathcal{P}.$
Comme $\mathcal{Q}$ contient le point $O$ de $\mathcal{D'}$, $\mathcal{Q}$ contient $\mathcal{D'}.$
De même $\mathcal{Q}$ contient $\Delta'.$
D'où $\mathcal{Q}=(\mathcal{D'}\;,\ \Delta').$
Théorème 9 :
Lorsque deux plans sont parallèles et distincts,
$-\ \ $ Tout plan parallèle à l'un est aussi parallèle à l'autre.
$-\ \ $ Tout plan qui coupe l'un coupe l'autre et les droites d'intersection sont parallèles.
Démonstration :
1) Supposons que $\mathcal{P}\parallel\mathcal{Q}$ et $\mathcal{R}\parallel\mathcal{P}.$
Si $\mathcal{R}$ coupait $\mathcal{Q}$, soit $O$ un point de $\mathcal{R}\cap\mathcal{Q}.$
Par $O$ passeraient deux plans $\mathcal{Q}$ et $\mathcal{R}$ parallèles à $\mathcal{P}$, ce qui contredit le théorème 7.
Donc $\mathcal{R}\parallel\mathcal{Q}.$
2)
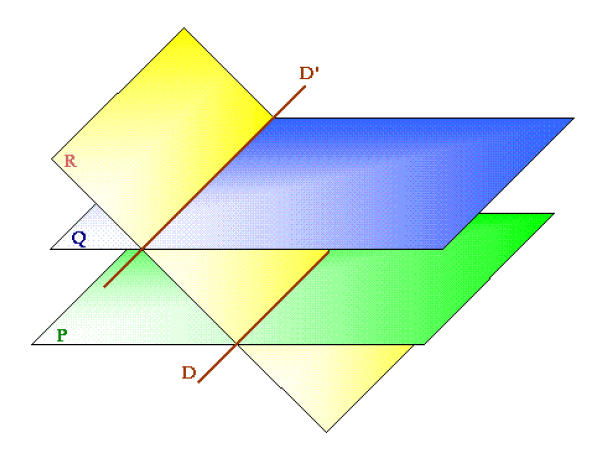
Si $\mathcal{P}\parallel\mathcal{Q}$ et $\mathcal{R}$ coupe $\mathcal{P}$, alors $\mathcal{R}$ n'est pas parallèle à $\mathcal{Q}$, sinon il serait parallèle à $\mathcal{P}$ (d'après 1), ce qui est absurde.
$\mathcal{R}$ n'est pas non plus confondu avec $\mathcal{Q}$ puisqu'il coupe $\mathcal{P}.$
Donc $\mathcal{R}$ coupe $\mathcal{Q}.$
Les droites d'intersection $\mathcal{D}$ et $\mathcal{D'}$ sont toutes deux dans le même plan $\mathcal{R}$ et n'ont pas de point commun puisque $\mathcal{D}\cup\mathcal{P}$ et $\mathcal{D'}\cup\mathcal{Q}$ avec $\mathcal{P}\parallel\mathcal{Q}.$
Donc elles sont parallèles.
Théorème 10 :
Lorsque deux plans sont parallèles et distincts,
$-\ \ $ Tout droite parallèle à l'un est aussi parallèle à l'autre.
$-\ \ $ Tout droite qui coupe l'un coupe l'autre.
Démonstration :
1) Si $\Delta\parallel\mathcal{P}$, $\Delta$ ne peut couper $\mathcal{Q}$ sans quoi il couperait aussi $\mathcal{P}$, d'après le 2) du théorème 8, ce qui est contraire à l'hypothèse.
Donc $\Delta$ est parallèle à $\mathcal{P}$ (ou contenue dans $\mathcal{Q}).$
2) Si $\mathcal{D}$ coupe $\mathcal{P}$ en $A$, $\mathcal{D}$ n'est pas parallèle à $\mathcal{Q}$ car sinon elle serait dans le plan passant par $A$ et parallèle à $\mathcal{Q}$, c'est-à-dire le plan $\mathcal{P}$ : absurde.
De plus, $\mathcal{D}$ n'est pas incluse dans $\mathcal{Q}$, car $\mathcal{D}$ passe par le point $A$ de $\mathcal{P}.$
Donc $\mathcal{D}$ coupe $\mathcal{P}.$
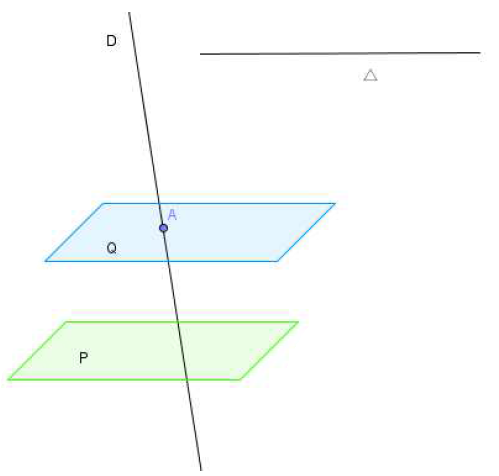
VI. Projection dans l'espace
1) Projection sur un plan parallèlement à une droite
Définition :
$M$ étant un point de l'espace, $\Delta$ une droite de l'espace et $\mathcal{P}$ un plan de l'espace, on appelle projeté de $M$ sur $\mathcal{P}$ parallèlement à $\Delta$ le point $M'$ d'intersection de $\mathcal{P}$ avec la droite passant par $M$ et parallèle à $\Delta.$
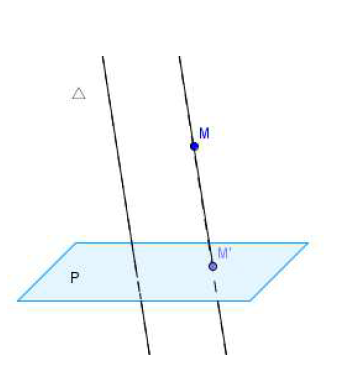
Remarques :
$-\ \ $ Tous les points d'une droite parallèle à $\Delta$ ont le même projeté sur $\mathcal{P}.$
$-\ \ $ Tout point $M$ de $\mathcal{P}$ est son propre projeté.
2) Projection sur une droite parallèlement à un plan
Définition :
$M$ étant un point de l'espace, $\Delta$ une droite de l'espace et $\mathcal{P}$ un plan de l'espace non parallèle à $\Delta$, on appelle projeté de $M$ sur $\Delta$ parallèlement à $\mathcal{P}$ le point $M'$ d'intersection de $\Delta$ avec le plan $\mathcal{P}_{M}$ passant par $M$ et parallèle à $\mathcal{P}.$
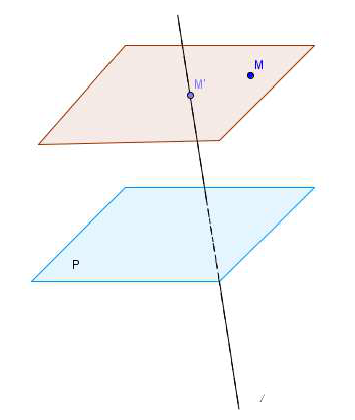
3) Théorème de THALES dans l'espace
Nous admettrons que, comme dans le plan, toute droite $\mathcal{D}$ de l'espace peut être munie d'une orientation en choisissant sur elle une origine, une unité et un sens de parcours, ce qui en fait un axe.
On définit alors la mesure algébrique d'un couple de points de $\mathcal{D}$ de la même manière que dans le plan.
Théorème 11 :
Soit $\mathcal{P}$, $\mathcal{Q}$ et $\mathcal{R}$ trois plans strictement parallèles, $\Delta$ et $\Delta'$ deux droites distinctes qui coupent $\mathcal{P}$, $\mathcal{Q}$ et $\mathcal{R}$ en $A$, $B$ et $C$, et $A'$, $B'$ et $C'$ respectivement, alors on a :
$$\dfrac{\overline{AB}}{\overline{AC}}=\dfrac{\overline{A'B'}}{\overline{A'C'}}.$$
Démonstration :
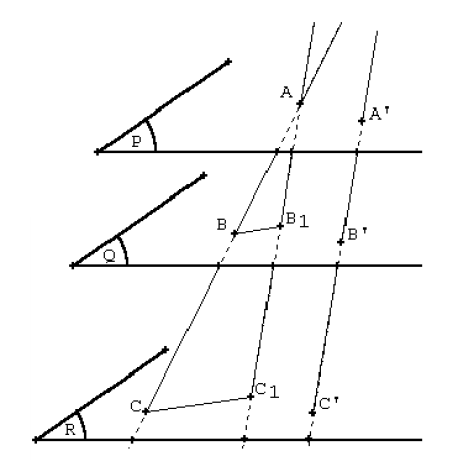
Auteur:
Ka, Faye & Mbengue

Ajouter un commentaire