Devoir n° 6 - Ts1

 

Soit $f$ une fonction deux fois dérivables sur $[-2\ ;\ 3]$

 

La courbe ci-dessous est celle de $f'$ $($fonction dérivée de $f).$

 

 

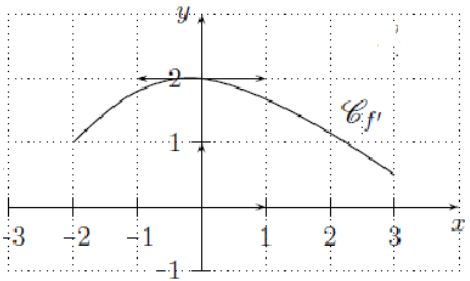
Répondre par Vrai ou Faux en justifiant la réponse :

 

$\bullet\ 1)\ f(-)<f(2)$

 

$\bullet\ 2)$ La courbe $\left(\mathcal{C}_{f}\right)$ admet une tangente parallèle à l'axe des abscisses

 

$\bullet\ 3)\ \left|f(3)-f(-2)\right|\leq 10$

 

$\bullet\ 4)\ f$ réalise une bijection de $[-2\;,\ 3]$ sur $f\left([-2\;,\ 3]\right)$

 

Exercice 2

 

1) On veut former des nombres à cinq chiffres distincts avec les chiffres : 

 

$0\;,\ 1\;,\ 2\;,\ 3\;,\ 4\;,\ 5\;,\ 6\;,\ 7\;,\ 8\;,\ 9$

 

a) Combien de nombres distincts peut-on ainsi former ?

 

b) Dénombrer les cas possibles si :

 

i. Le chiffre des unités est un nombre premier.

 

ii. Le nombre formé est pair.

 

iii. Le nombre formé comprend le chiffre $2.$

 

Exercice 3

 

Déterminer les branches infinies de la courbe $\mathcal{C}$ des fonctions $f$ telles que :

 

1) $f(x)=\sqrt{x^{2}-1}-\sqrt{x^{2}+x-7}$

 

2) $f(x)=\dfrac{\sqrt{x^{2}+x-7}-\sqrt{x^{2}-1}}{2x+1}$

 

3) $f(x)=x-3\tan x$

 

4) $f(x)=\dfrac{x}{\sin x}$

 

Exercice 4

 

Les deux questions de cet exercice sont totalement inde pendantes

 

1) On considère la fonction $f$ de finie par :

$$\left\lbrace\begin{array}{lcl} f(x)&=&x\sin\left(\dfrac{1}{x}\right)\quad;\quad x>0\\ f(0)&=&1\\ f(x)&=&xE\left(\dfrac{1}{x}\right)\quad;\quad x<0  \end{array}\right.$$

 

a) Étudier la continuité de $f$ en $0.$

 

b) Calculer $\lim\limits_{|x|\longrightarrow\;+\infty}f(x)$

 

2) Soit $f$ une fonction continue sur un segment $[a\ ;\ b].$

 

Montrer qu'il existe $c\in[a\ ;\ b]$ tel que : $2f(a)+3f(b)=5f(c).$

 

Exercice 5

 

A) Dans la figure ci-dessous :

 

$\bullet\ \mathcal{C}$ est la courbe représentative dans un repère orthonormé d'une fonction $f$,

 

$\bullet\ \Gamma$ est la courbe de sa fonction dérivée.

 

$\bullet\ $L'axe des abscisses est une asymptote commune à $\mathcal{C}$ et $\Gamma$ au voisinage de +$+\infty$

 

$\bullet\ $La droite $\Delta$ est une asymptote à $\mathcal{C}$ au voisinage de $-\infty$

 

 

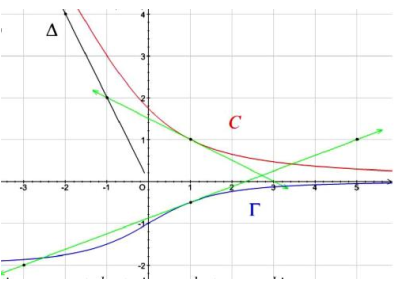
Par lecture graphique, déterminer :

 

1) $\lim\limits_{x\longrightarrow\;+\infty}f(x)\quad\text{et}\quad\lim\limits_{x\longrightarrow\;+\infty}f'(x)$

 

2) $\lim\limits_{x\longrightarrow\;-\infty}f(x)$,

 

$\lim\limits_{x\longrightarrow\;-\infty}\dfrac{f(x)}{x}$,

 

$\lim\limits_{x\longrightarrow\;-\infty}\dfrac{f\circ f(x)}{f(x)}$

 

et $\lim\limits_{x\longrightarrow\;-\infty}\left(f(x)+2x+1\right)$

 

3) $f(1)\;,\ f'(1)\quad\text{et}\quad f''(1)$

 

On donne $f(x)=\sqrt{x^{2}+3}-x$

 

1) a) Calculer $f'(x)$ pour $x\in\mathbb{R}$

 

b) Calculer $f''(x)$ pour $x\in\mathbb{R}$ et en déduire que $f'$ est strictement croissante sur $\mathbb{R}$

 

c) En appliquant le théorème des accroissement finis, montrer que pour tout $x\in\left[\dfrac{1}{2}\;,\ 2\right]$ on a :

 

$\left|f(x)-1\right|\leq\dfrac{3}{4}\left|x-1\right|$

 

2) Soit la fonction $g$ continue sur $[0\;,\ 1]$, dérivable sur $]0\;,\ 1]$ tel que : $g(0)=1$ et $g(1)=\sqrt{3}$

 

a) Montrer qu'il existe au moins un réel $a\in]0\;,\ 1[$ tel que $f(a)=g(a)$

 

b) Montrer qu'il existe au moins un réel $b\in]0\;,\ 1[$ tel que $f'(b)=-g'(b)$

 

3) On pose $u(x)=x\sin\left(\dfrac{2}{x}\right)\quad\text{et}\quad v(x)=-\dfrac{1}{x^{2}}+\cos\left(\dfrac{1}{x}\right)$

 

a) A l'aide des théorèmes de comparaison, étudier les limites en $0$ des fonctions $u$ et $v.$

 

b) Calculer $\lim\limits_{x\longrightarrow\;+\infty}\left(u\circ f\right)(x)\quad\text{et}\quad \lim\limits_{x\longrightarrow\;0}\left(f\circ v\right)(x)$