Devoir math n°17 - 2nd

 

 

Exercice 1

 

$ABCD$ est un parallélogramme, $J$ est le milieu de $[AD]$, $P$ et $I$ sont 

 

 

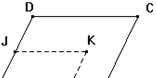
Les points tels que $\overrightarrow{AP}=\dfrac{1}{3}\overrightarrow{AB}$ et $\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}$ ; $K$ est le point tel que le quadrilatère $AIKJ$ soit un parallélogramme

 

1. Soit $G$ le barycentre de $(A\;,\ 1)$, $(B\;,\ 2)$ et $(D\;,\ 1)$

 

a. Construire $G$

 

b. Écrire $I$ comme le barycentre de $A$ et $B$

 

c. Montrer que les droites $(BJ)$ et $(ID)$ se coupent en $G$

 

2.a. Exprimer $C$ et $K$ comme barycentre de $A$, $B$ et $D$

 

b. En déduire $\overrightarrow{GC}$ et $\overrightarrow{GK}$ en fonction de $\overrightarrow{GA}$, $\overrightarrow{GB}$ et $\overrightarrow{GD}.$

 

c. Montrer que les droites $(BJ)$, $(ID)$ et $(CK)$ sont concourantes

 

3.a. Exprimer $D$ comme barycentre de $A$, $B$, $C$ et $P$ comme barycentre de $A$ et $B$

 

b. Montrer que les points $P$, $G$ et $C$ sont alignés

 

Exercice 2

 

$ABCD$ est un rectangle tel que $AB=4$ et $AD=3$

 

1. Déterminer et construire le barycentre $G$ des points $(A\ ;\ 1)$, $(B\ ;\ 1)$ et $(C\ ;\ 1)$

 

2. Déterminer et construire l'ensemble $E$ des points $M$ du plan tels que $||\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}||=5$

 

3. Déterminer et construire l'ensemble $F$ des points $M$ du plan tels que $MA^{2}-MB^{2}+MC^{2}=\dfrac{25}{4}$

 

4. Déterminer et construire l'ensemble $H$ des points $M$ du plan tels que $MA^{2}+MB^{2}+MC^{2}+MD^{2}=61$

 

Exercice 3

 

Dans un repère orthonormé $\left(O\;,\ \vec{i}\;,\ \vec{j}\right)$ du plan, on considère le cercle $(\mathcal{C})$ passant par les points $A(4\ ;\ 2)$, $B(2\ ;\ 6)$ et dont le centre $\Omega$ est situé sur la droite $(\mathcal{D})$ d'équation $x+y+2=0.$

 

1. Faire une figure ;

 

2. Déterminer les coordonnées de $\Omega$ puis donner une équation cartésienne de $(\mathcal{C})$ 

 

3. On considère les points $C(7\ ;\ 0)$ et $D(0\ ;\ 3)$ 

 

Donner une représentation paramétrique de la droite $(CD)$ puis déterminer les points d'intersection de $(CD)$ et $(\mathcal{C})$

 

Exercice 4 les questions 1 et 2 sont indépendantes

 

1. $ABC$ est un triangle isocèle en $A$ $D$ est le milieu de $[BC]$, $E$ est le projeté orthogonal de $D$ sur $(AC)$ et $F$ est le milieu de $[DE]$

 

a. Faire une figure

 

b. Montrer que les droites $(AF)$ et $(BE)$ sont perpendiculaires

 

2. $A$ et $B$ sont deux points du plan tels que $AB=6\,cm.$

 

Déterminer et construire :

 

a. L'ensemble $H_{1}$ des points $M$ du plan tels que $\overrightarrow{MA}\cdot\overrightarrow{MB}=-5$

 

b. L'ensemble $H_{2}$ des points $M$ du plan tels que $MA^{2}-MB^{2}=-36$

 

c. L'ensemble $H_{3}$ des points $M$ du plan tels que $5MA^{2}-3MB^{2}=-220$