Corrigé Exercice 3 : Distances - 4e
Classe:
Quatrième
Exercice 3 Inégalité triangulaire
Soit $ABC$ un triangle et $M$ un point intérieur à ce triangle. La droite $(AM)$ coupe $[BC]$ en $I.$
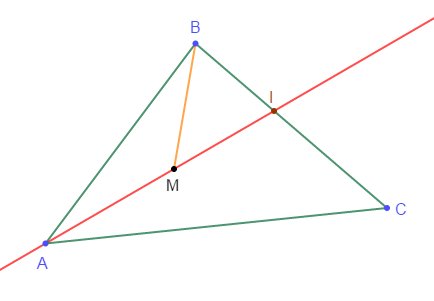
1) a) Démontrons que $IC+IB=BC\ $ et $\ IA<IC+CA.$
Comme la droite $(AM)$ coupe $[BC]$ au point $I$ alors, $I\in[BC]$
Ce qui entraine : $\boxed{IC+IB=BC}$
Par ailleurs, en appliquant l'inégalité triangulaire sur le triangle $IAC$, on obtient : $\boxed{IA<IC+CA}$
b) En déduisons que : $IA+IB<CA+CB.$
On a : $IA<IC+CA$
Donc, en ajoutant $IB$ à chaque membre de l'inégalité, on obtient : $IA+IB<IB+IC+CA$
Or, $\ IC+IB=BC$ donc, en remplaçant $IC+IB$ par $BC$, on trouve : $IA+IB<BC+CA$
Ainsi, $\boxed{IA+IB<CA+CB}$
2) Démontrons que : $MA+MB<IA+IB.$
En appliquant l'inégalité triangulaire sur le triangle $BMI$, on obtient : $MB<IM+IB$
Puis, en ajoutant $MA$ à chaque membre de l'inégalité, on obtient : $MA+MB<MA+IM+IB$
Comme $M\in[IA]$ alors, $IM+MA=IA$
Donc, en remplaçant $IM+MA$ par $IA$, on obtient : $MA+MB<IA+IB$
D'où, $\boxed{MA+MB<IA+IB}$
3) Déduisons de ce qui précède que : $MA+MB<CA+CB.$
D'après la question 2) on a : $MA+MB<IA+IB$
Or, d'après la question 1) on avait : $IA+IB<CA+CB$
Par suite, $MA+MB<IA+IB\ $ et $\ IA+IB<CA+CB$
Par conséquent, $\boxed{MA+MB<CA+CB}$

Ajouter un commentaire