Corrigé Exercice 23 : Théorème de Thalès - 3e

 

Sur la figure ci-dessous, 

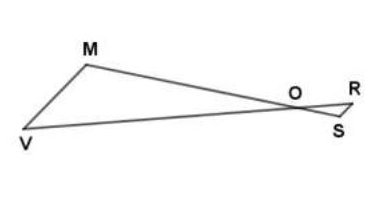
$MO=7.5\;cm$, $OV=18\;cm$, $OS=1.5\;cm$ et $OR=3.6\;cm$, $RS=3\;cm.$

 

1) Montrons que les droites $(MV)\ $ et $\ (RS)$ sont parallèles.

 

On a : $M\;,\ O\;,\ S$ sont trois points alignés d'une part, et $V\;,\ O\;,\ R$ sont trois points alignés d'autre part, dans le même ordre.

 

En calculant les rapports $\dfrac{OS}{MO}\ $ et $\ \dfrac{OR}{OV}$, on a :

 

$\dfrac{OS}{MO}=\dfrac{1.5}{7.5}=0.2$

 

$\dfrac{OR}{OV}=\dfrac{3.6}{18}=0.2$

 

On remarque alors que : $\dfrac{OS}{MO}=\dfrac{OR}{OV}.$

 

Par conséquent, d'après la réciproque du théorème de Thalès, les droites $(MV)\ $ et $\ (RS)$ sont parallèles.

 

2) Calculons $VM.$

 

Comme les droites $(MV)\ $ et $\ (RS)$ sont parallèles alors, les triangles $OMV\ $ et $\ ORS$ sont en position de Thalès.

 

Ainsi, en appliquant le théorème de Thalès, on a :

$$\dfrac{RS}{VM}=\dfrac{OR}{OV}$$

Or, $\dfrac{OR}{OV}=0.2$

 

Donc, en remplaçant $RS\ $ et $\ \dfrac{OR}{OV}$ par leur valeur, on obtient :

 

$\begin{array}{rcl}\dfrac{3}{VM}=0.2&\Leftrightarrow&0.2\times VM=3\\\\&\Leftrightarrow&VM=\dfrac{3}{0.2}\\\\&\Leftrightarrow&VM=15\end{array}$

 

D'où, $\boxed{VM=15\;cm}$