Corrigé du baccalauréat S - Polynésie - 2 septembre 2020
Exercice 1
Commun à tous les candidats
1.Une urne contient $5$ boules rouges et $3$ boules blanches indiscernables au toucher.
On extrait une boule de l'urne et on note sa couleur.
On répète $4$ fois cette expérience,de manière indépendante,en remettant la boule à chaque
fois dans l'urne.
La probabilité, arrondie au centième,d'obtenir au moins $1$ boule blanche est:
Réponse $A\ :\ 0.15$
Réponse $B\ :\ 0.63$
Réponse $C\ :\ 0.5$
Réponse $D\ :\ 0.85$
Il y a $3$ boules blanches sur un total de $8$ boules,donc la probabilité de prendre une boule
blanche est $\dfrac{3}{8}$
La variable aléatoire $X$ qui donne le nombre de boules blanches tirées parmi $4$ suit une loi
binomiale de paramètres $n=4$ et $P=\dfrac{3}{8}$
La probabilité d'obtenir au moins $1$ boule blanche est:
$\begin{array}{rcl}P\left(X\geq 1\right)&=&1-P\left(X=0\right)\\&=&1-\left(\dfrac{5}{8}\right)^{4}\\&\approx&0.85 \end{array}$
2. Soit $n$ étant un entier naturel supérieur ou égal à $2$
Un sac contient $n$ pièces indiscernables au toucher.
Ces pièces comportent toutes un côté
« PILE » et un côté « FACE » sauf une qui contient deux côtés « FACE ».
On choisit au hasard une pièce du sac puis on la lance.
La probabilité d'obtenir le côté « FACE » est égale à:
Réponse $A\ :\ \dfrac{n-1}{n}$
Réponse $B\ :\ \dfrac{n+1}{2n}$
Réponse $C\ :\ \dfrac{1}{2}$
Réponse $D\ :\ \dfrac{n-1}{2n}$
Soient les événements
$\bullet\ N$ « la pièce est normale,c'est-à-dire à deux côtés PILE et FACE »
$\bullet\ F$ : « le côté obtenu est FACE »
On représente la
situation au moyen de l'arbre pondéré suivant:
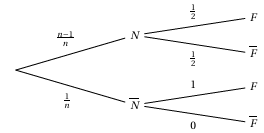
$\begin{array}{rcl} P(F)&=&P\left(N\cap F\right)+P\left(P\overline{N}\cap F\right)\\&=&\dfrac{n-1}{n}\times \dfrac{1}{2}+\dfrac{1}{n}\times 1\\&=&\dfrac{n-1}{2n}+\dfrac{2}{2n}\\&=&\dfrac{n-1+2}{2n}\\&=&\dfrac{n+1}{2n}
\end{array}$
3. On considère $T$ la variable aléatoire suivant la loi normale d'espérance $\mu=60$ et d'écart-type $\delta=6$
La probabilité $P_{\left(T> 60\right)}\left(T> 72\right)$ arrondie au millième est :
Réponse $A\ :\ 0.954$
Réponse $B\ :\ 1$
Réponse $C\ :\ 0.023$
Réponse $D\ :\ 0.046$
$\begin{array}{rcl} P_{\left(T> 60\right)}\left(T> 72\right)&=&\dfrac{P\left(\left(T> 60\right)\cap\left(T> 72\right)\right)}{P\left(T> 60\right)}\\&=&\dfrac{P\left(T> 72\right)}{P\left(T> 60\right)}\\&\approx&\dfrac{0.02275}{0.5}\\&\approx&0.046 \end{array}$
4. La durée de fonctionnement, exprimée en années, d'un moteur jusqu'à ce que survienne la
première panne est modélisée par une variable aléatoire suivant une loi exponentielle de par a
mètre $\lambda$ où $\lambda$ est un réel strictement positif.
La probabilité que le moteur fonctionne sans panne pendant plus de 3 ans est égale à
Réponse $A\ :\ \mathrm{e}^{-3\lambda}$
Réponse $B\ :\ 1-\mathrm{e}^{-3\lambda}$
Réponse $C\ :\ \mathrm{e}^{3\lambda}-1$
Réponse $D\ :\ \mathrm{e}^{3\lambda}$
D'après le cours, $P\left(X\geq t\right)=\mathrm{e}^{-\lambda t}$ donc la probabilité cherchée est $\mathrm{e}^{-3\lambda}$
5. On note $X$ une variable aléatoire suivant la loi uniforme sur $\left[0\ ;\ \dfrac{\pi}{2}\right]$ la probabilité qu'une valeur prise par la variable aléatoire $X$ soit solution de l'inéquation $\cos x>\dfrac{1}{2}$ est égale à :
Réponse $A\ :\ \dfrac{2}{3}$
Réponse $B\ :\ \dfrac{1}{3}$
Réponse $C\ :\ \dfrac{1}{2}$
Réponse $D\ :\ \dfrac{1}{\pi}$
Sur $\left[0\ ;\ \dfrac{\pi}{2}\right]$, on a $\cos x>\dfrac{1}{2}$ pour $x\in\left[0\ ;\ \dfrac{\pi}{3}\right]$
La probabilité cherchée est
$\begin{array}{rcl} \dfrac{\dfrac{\pi}{3}-0}{\dfrac{\pi}{2}-0}&=&\dfrac{\dfrac{\pi}{3}}{\dfrac{\pi}{2}}\\&=&\dfrac{\pi}{3}\times \dfrac{2}{\pi}\\&=&\dfrac{2}{3} \end{array}$
Exercice 2
Soit $ABCDEFGH$ un cube.
L'espace est rapporté au repère orthonormé $\left(A\ ;\ \overrightarrow{AB}\;,\overrightarrow{AD}\;,\overrightarrow{AE}\right)$
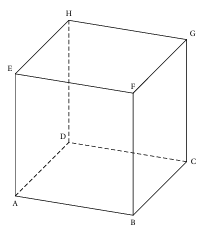
Pour tout réel $t$, on considère le point $M$ de coordonnées $(1-t\ ;\ t\ ;\ t)$
1. Le point $B$ a pour coordonnées $(1\ ;\ 0\ ;\ 0)$ comme $\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{AE}$, le point $H$ pour coordonnées $(0\ ;\ 1\ ;\ 1)$
Le vecteur $\overrightarrow{BM}$ a pour coordonnées $(1-t-1\ ;\ t-0\ ;\ t-0)$ soit $(-t\ ;\ t\ ;\ t)$
Le vecteur $\overrightarrow{BH}$ a pour coordonnées $(0-1\ ;\ 1-0\ ;\ 1-0)$ soit $(-1\ ;\ 1\ ;\ 1)$
On a donc $\overrightarrow{BM}=t\overrightarrow{BH}$,donc les vecteurs $\overrightarrow{BM}$ et $\overrightarrow{BH}$ sont colinéaires, ce qui prouve que le point $M$ appartient à la droite $(BH)$ pour tout réel $t$
On admet que les droites $(BH)$ et $(FC)$ sont respectivement pour représentation paramétrique :
$\left\lbrace\begin{array}{rcl} x&=&1-t\\ y&=&t\\ z&=&t \end{array}\right.\text{ où }t\in\mathbb{R}$
et $\left\lbrace\begin{array}{rcl} x&=&1\\ y&=&t'\\ z&=&1-t' \end{array}\right.\text{ où }t'\in\mathbb{R}$
2. On va démontrer que les droites $(BH)$ et $(FC)$ sont orthogonales et non coplanaires.
$\bullet\ $D'après sa représentation paramétrique, la droite $(BH)$ est dirigée par le vecteur $\overrightarrow{n}$ coordonnées $(-1\ ;\ 1\ ;\ 1)$
D'après sa représentation paramétrique, la droite ($(FC)$ est dirigée par le vecteur $\vec{n'}$ coordonnées $(0\ ; 1\ ;\ -1)$
On en déduit que les droites $(BH)$ et $(FC)$ sont orthogonales.
$\bullet\ $Si les droites les droites $(BH)$ et $(FC)$ sont coplanaires, comme elles sont orthogonales, elles seront sécantes ; il suffit donc de prouver que les droites $(BH)$ et $(FC)$ ne sont pas sécantes pour démontrer qu'elles ne sont pas coplanaires.
Les droites $(BH)$ et $(FC)$ sont sécantes si on peut trouver $t$ et $t'$ tels que:
Ce système n'a pas de solution donc les droites $(BH)$ et $(FC)$ ne sont pas sécantes, donc
elles ne sont pas coplanaires.
3. Pour tout réel $t'$, on considère le point $M'\left(1\ ;\ t'\ ;\ 1-t'\right)$
a. $\begin{array}{rcl} MM^{'2}&=&(1-1+t)^{2}+\left(t'-t\right)^{2}+\left(1-t^{1}-t\right)^{2}\\&=&t^{2}+t^{'2}-2tt'+t^{2}+1-t'-t-t'+t'^{2}+tt'-t+tt'+t^{2}\\&=&3t^{2}+2t'^{2}-2t'-2t+1 \end{array}$
$\begin{array}{rcl} 3\left(t-\dfrac{1}{3}\right)+2\left(t'-\dfrac{1}{2}\right)^{2}+\dfrac{1}{6}&=&3\left(t^{2}-\dfrac{2t}{2}+\dfrac{1}{9}\right)+2\left(t^{'2}-\dfrac{2t'}{2}+\dfrac{1}{4}\right)+\dfrac{1}{6}\\&=&\left(t-\dfrac{1}{3}\right)^{2}+2\left(t'-\dfrac{1}{2}\right)^{2}+\dfrac{1}{6}\\&=&3\left(t^{2}-\dfrac{2t}{3}+\dfrac{1}{9}\right)+2\left(t^{'2}-\dfrac{2t'}{2}+\dfrac{1}{4}\right)+\dfrac{1}{6}\\&=&3t^{2}-2t+\dfrac{1}{3}+2t^{'2}-2t'+\dfrac{1}{2}+\dfrac{1}{6}\\&=&3t^{2}+2t^{'2}-2t'-2t \end{array}$
b. La distance $MM'$ est minimale quand $MM^{'2}$ est minimale.
$MM^{'2}$ est la somme de trois nombres positifs ou nuls, et sera minimale quand chacun de
ces nombres est minimal.
$\bullet\ 3\left(t-\dfrac{1}{3}\right)^{2}$ est minimale et vaut $0$ pour $t=\dfrac{1}{3}$ ;
$\bullet\ 2\left(t'-\dfrac{1}{2}\right)^{2}$ est minimal et vaut $0$ pour $t'=\dfrac{1}{2}$
Donc $MM'$ est minimale pour $t=1$ et $t'=\dfrac{1}{2}$ ; dans ce cas $$MM'=\sqrt{\dfrac{1}{6}}$
c. On nomme $P$ le point de coordonnées $\left(\dfrac{2}{3}\ ;\ \dfrac{1}{3}\ ;\ \dfrac{1}{3}\right)$ et $Q$ celui de coordonnées
$\left(1\ ;\ \dfrac{1}{2}\ ;\ \dfrac{1}{2}\right)$
$\bullet\ $ Le point $P$ appartient à la droite $(BH)$ pour $t=3$, donc $(BP)=(BH)$
$\bullet\ $Le point $Q$ appartient à la droite $(FC)$ pour $t'=\dfrac{1}{2}$ donc $(QC)=(BH)$
$\bullet\ $Le vecteur $\overrightarrow{PQ}$ a pour coordonnées $\left(1-\dfrac{2}{3}\ ;\ \dfrac{1}{2}-\dfrac{1}{3}\ ;\ \dfrac{1}{2}-\dfrac{1}{3}\right)=\left(\dfrac{1}{3}\ ;\ \dfrac{1}{6}\ ;\ \dfrac{1}{6}\right)$
$\bullet\ $Le vecteur $\overrightarrow{BP}$ a pour coordonnées $\left(\dfrac{2}{3}-1\ ;\ \dfrac{1}{3}-0\ ;\ \dfrac{1}{3}-0\right)=\left(-\dfrac{1}{3}\ ;\ \dfrac{1}{3}\ ;\ \dfrac{1}{3}\right)$$
$\bullet\ $ $\begin{array}{rcl} BP\cdot\overrightarrow{PQ}&=&\left(-\dfrac{1}{3}\right)\left(\dfrac{1}{3}\right)+\left(\dfrac{1}{3}\right)\left(\dfrac{1}{6}\right)+\left(\dfrac{1}{3}\right)\left(\dfrac{1}{6}\right)\\&=&-\dfrac{1}{9}+\dfrac{1}{18}+\dfrac{1}{18}\\&=&0 \end{array}$ donc $\overrightarrow{BP}\perp\overrightarrow{PQ}$ donc la droite $(PQ)$ est perpendiculaire à la droite $(BP)$ donc à la droite $(BH)$
$(PQ)$ est perpendiculaire à la droite $(QC)$ donc à la droite $(FC)$
Donc la droite $(PQ)$ est perpendiculaire aux deux droites $(BH)$ et $(FC)$
Exercice 3
Commun à tous les candidats
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x\mathrm{e}^{-x^{2+1}}$
On note $(\mathfrak{C})$ la courbe représentative de $f$ dans un repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\right)$
1.a. Pour tout $x$ réel,
$\begin{array}{rcl} f(x)&=&x\mathrm{e}^{-x^{2}+1}\\&=&x\mathrm{e}^{-x}^{2}\times \mathrm{e}\\&=&\dfrac{x}{\mathrm{e}^{x^{2}}}\times\mathrm{e}\\&=&\dfrac{\mathrm{e}}{x}\times\dfrac{x^{x}}{\mathrm{e}^{x^{2}}} \end{array}$
b $\bullet\ \begin{array}{rcl} \lim\limits_{x\longrightarrow\,+\infty}\dfrac{1}{x}&=&0&\\ &\text{ donc }&\lim\limits_{x\longrightarrow+\infty}\dfrac{\mathrm{e}}{x}\\&=&0 \end{array}$
$\bullet\ $ pour tout réel $X$, $\begin{array}{rcl} \lim\limits_{x\longrightarrow+\infty}\dfrac{e^{X}}{X}&=&+\infty\\&\text{ donc }&\lim\limits_{X\longrightarrow+\infty}\dfrac{X}{\mathrm{e}^{X}}\\&=&0 \end{array}$
Or $\lim\limits_{x\longrightarrow+\infty}x^{x}=+\infty$, donc en posant $X=x^{2}$, on déduit que $\lim\limits_{x\longrightarrow+\infty}\dfrac{x^{2}}{\mathrm{e}^{x^{2}}}=0$
Par produit de limites,on déduit que $\lim_{x\longrightarrow+\infty}\dfrac{x^{2}}{\mathrm{e}^{x^{2}}}=0$
Pour tout réel $x$,on considère les points $M$ et $N$ de la courbe $(C)$ d'abscisses respectives $x$ et $-x$
a. Les coordonnées de $M$ sont $(x\ ;\ f(x))$ et celles de $N$ sont $(-x\ ;\ f(-x))$
Le milieu de $[MN]$ a pour coordonnées $\left(\dfrac{x+(-x)}{2}\ ;\ \dfrac{f(x)+(-f(x))}{2}\right)=(0\ ;\ 0)$
C'est donc le point $0$
b. La courbe (C est donc symétrique par rapport au point $0$
3. La fonction $f$ est dérivable sur l'intervalle $[0\ ;\ +\infty[$ et
$\begin{array}{rcl} f'(x)&=&1\times\mathrm{e}^{-x^{2}+1}+x\times (-2x)\mathrm{e}^{-x^{2}+1}\\&=&\left(1-2x^{2}\right)\mathrm{e}^{-x^{2}+1} \end{array}$
Pour tout réel $x$, $\mathrm{e}^{-x^{2}+1}>0$ donc $f'(x)$
est du signe de $1-2x^{2} $ qui s'annule et change de signe pour $x=\dfrac{\sqrt{2}}{2}$ sur $[0\ ;\ +\infty[$
$\begin{array}{rcl} f(0)&=&0\\&\text{ et }&f\left(\dfrac{\sqrt{2}}{2}\right)\\&=&\dfrac{\sqrt{2}}{2}\mathrm{e}^{-\left(\dfrac{\sqrt{2}}{2}\right)^{2}+1}\\&=&\dfrac{\sqrt{2}}{2}\mathrm{e}^{\dfrac{1}{2}}\\&=&\dfrac{\sqrt{2e}}{2}\\&\approx&1.166 \end{array} $
D'où le tableau des variations de $f$ sur l'intervalle $[0\ ;\ +\infty[$ :
$\begin{array}{|c|ccccc|} \hline x&0&&\dfrac{\sqrt{2}}{2}&&+\infty\\ \hline 1-2x^{2}&&+&\mid&-&\\ \hline f'(x)&&+&\mid&-&\\ \hline &&&\dfrac{\sqrt{2\mathrm{e}}}{2}&&\\ f(x)&&\nearrow&&\searrow&\\ &0&&&&0\\ \hline \end{array}$
a. Le maximum de la fonction $f$ sur $[0\ ;\ +\infty[$ est $\dfrac{\sqrt{2e}}{2}$ qui est supérieur à $0.5$
On complète le tableau de variations de $f$,ce qui prouve que l'équation $f(x)=0.5$ admet
sur $[0\ ;\ +\infty[$ exactement deux solutions notées $\alpha$ et $\beta(\text{ avec }\alpha<\beta)$
$\begin{array}{|c|ccccccccc|} \hline x&0&&\alpha&\dfrac{\sqrt{2}}{2}&&\beta&&+\infty\\ \hline &&&\vdots&\dfrac{\sqrt{2\mathrm{e}}}{2}&&\vdots&&&\\ f(x)&&&0.5\nearrow&&\diagdown&0.5&\searrow&&\\ &0&\diagup&&&&&&0\\ \hline \end{array}$
b. D'après le tableau de variations, on déduit que les solution sur $[0\ ;\ +\infty[$ de l'inéquation $fx)\geq 0.5$ son les éléments de l'intervalle $[\alpha\ ;\ \beta]$
c. A la calculatrice, on trouve $\alpha\approx 0.19$ et $\beta\approx1.43$
5. Soit $A$ un réel strictement positif.
On pose $I_{A}=\int_{0}^{A}f(x)dx$
a. Pour calculer $I_{A}=\int_{0}^{A}f(x)dx$, on cherche une primitive $F$ de $f$
La dérive de la fonction $x\longmapsto\mathrm{e}^{u(x)}$ est la fonction $x_{\longmapsto}u'(x)e^{u(x)}$ ; donc la dérivé de $x\longmapsto\mathrm{e}^{-x^{2}+1}$ est $x\longmapsto xe^{-x^{2}+1}$
Dans la fonction $f$ a pour primitive la fonction $F$ définie par $F(x)=-\dfrac{1}{2}\mathrm{e}^{-x^{2}+1}$
$\begin{array}{rcl} I_{A}&=&\int_{0}^{A}f(x)dx\\&=&[F(x)]_{0}^{A}\\&=&F(A)-F(O)\\&=&-\dfrac{1}{2}\mathrm{e}^{-A^{2}+1}+\dfrac{1}{2}\mathrm{e}^{0+1}\\&=&\dfrac{1}{2}\left(\mathbb{e}-\mathbb{e}^{-A^{2}+1}\right) \end{array}$
b. $\begin{array}{rcl} \lim\limits_{A\longrightarrow+\infty}-A^{2}+1&=&-\infty\\&\text{ et }&\lim\limits_{x\longrightarrow-\infty}\mathrm{e}^{x}\\&=&0\\&\text{ donc }&\lim\limits_{A\longrightarrow+\infty}\mathrm{e}^{-A^{2}+1}\\&=&0 \end{array}$
On en déduit que $\lim\limits_{A\longrightarrow+\infty}I_{A}=\dfrac{\mathrm{e}}{2}$
On admet que cette limite est l'aire en unités d'aire située entre la partie de la courbe $(\mathbb{C})$ sur $[0\ ;\ +\infty[$ et l'axe des abscisses.
On appelle $A_{1}$ cette aire,donc d'après les questions précédentes, $\mathbb{A}_{1}=\dfrac{\mathrm{e}}{2}$
Comme illustré sur le graphique ci-dessous,
délimitée par:
$\bullet\ \mathbb{C}$ sur $\left(\mathbb{C'}\right)$ symétrique de $(\mathbb{C})$ par rapport à l'axe des abscisses
$\bullet\ $Le cercle de centre $\Omega\left(\dfrac{\sqrt{2}}{2}\ ;\ 0\right)$ et de rayon $0.5$ et son symétrique par rapport à l'axe des ordonnées.
On admet que le disque de centre $\Omega\left(\dfrac{\sqrt{2}}{2}\ ;\ 0\right)$ et de rayon $0.5$cet son symétrique par rapport à l'axe des ordonnées sont situés entièrement entre la courbe $\left(\mathbb{C}\right)$ et la courbe $\left(\mathbb{C'}\right)$
Pour des raisons de symétrie, l'aire cherchée est $4$ fois l'aire hachurée ci-dessous :
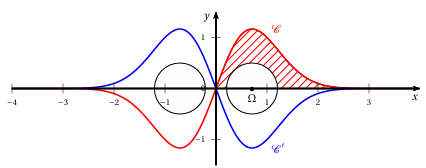
L'aire hachurée est égale à l'aire $A_{1}$ diminuée de l'aire $A_{2}$ du demi-disque de centre $\Omega$ et de rayon $0.5$
$\begin{array}{rcl} \mathbb{A}_{2}&=&\dfrac{\pi\times (0.5)^{2}}{2}\\&=&\dfrac{\pi}{8} \end{array}$
L'aire cherchée est donc $4\left(\mathbb{A}_{1}-\mathbb{A}_{2}\right)\\&=&4\left(\dfrac{\mathrm{e}}{2}-\dfrac{\pi}{8}\right)\\&=&2\mathrm{e}-\dfrac{\pi}{2}\\&\approx&3.87$ unité d'aire.
Exercice 4
Candidats n'ayant pas suivi l'enseignement de spécialité
Le plan complexe est muni d'un repère orthonormé direct $\left(O\ .\ \vec{u}\;,\vec{v}\right)$
On considère la suite de nombres complexes $\left(z_{n}\right)$ défini, par: $z_{0}=0$ et pour tout $n\;,z_{n+1}=(1+\mathrm{i})z_{n}-\mathrm{i}$
Pour tout entier naturel $n$, on note $A_{n}$ le point d'affixe $z_{n}$
On note $B$ le point d'affixe $1$
1.a. $\begin{array}{rcl} z_{1}&=&(1+i)z_{0}-i\\&=&(1+i)\times 0-i\\&=&-i \end{array}$
$\begin{array}{rcl} z_{2}&=&(1+i)z_{1}-i\\&=&(1+i)\times(-i)-i+1-i\\&=&1-2i \end{array}$
b. $\begin{array}{rcl} z_{3}&=&(1+i)z_{2}-i\\&=&(1+i)(1-2i)-i\\&=&1+i-2i+2-i\\&=&3-2i \end{array}$
c. On place les points $B$, $A_{1}$, $A_{2}$ et $A_{3}$ dans le repère orthonormé direct $\left(O\ ;\ \vec{u}\;,\vec{v}\right)$
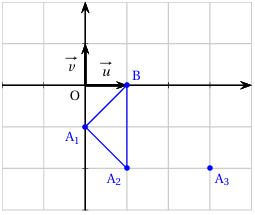
d. On démontre que le triangle $BA_{1}A_{2}$ est isocèle rectangle.
$\bullet\ \begin{array}{rcl} BA_{1}&=&\left|z_{1}-1\right|\\&=&\left|-i-1\right|\\&=&\sqrt{2} \end{array}$
$\begin{array}{rcl} A_{1}A_{2}&=&\left|z_{2}-z_{1}\right|\\&=&\left|-1-2i+i\right|\\&=&\left|-1-i\right|\\&=&\sqrt{2} \end{array}$
Donc l triangle $BA_{1}A_{2}$ est isocèle.
$\bullet\ \begin{array}{rcl} BA_{2}&=&\left|1-2i-1\right|\\&=&\left|-2i\right|\\&=&2 \end{array}$
$\begin{array}{rcl} BA_{1}^{2}+A_{1}A_{2}^{2}&=&\left(\sqrt{2}\right)^{2}+\left(\sqrt{2}\right)^{2}\\&=&2+2\\&=&4\\&=&BA_{2}^{2} \end{array}$ donc,d'après la réciproque du théorème de Pythagore, le triangle $BA_{1}A_{2}$ est rectangle en $A_{1}$
On a donc démontré que le triangle $BA_{1}A_{2}$ était isocèle rectangle en $A_{1}$
2. Pour tout entier naturel $n$, on pose $u_{n}=\left|z_{n}-1\right|$
a. $\begin{array}{rcl} u_{n+1}&=&\left|z_{n+1}-1\right|\\&=&\left|(1+i)z_{n}-i-1\right|\\&=&\left|(1+i)z_{n}-(1+i)\right|\\&=&\left|(1+i)\left(z_{n}-1\right)\right|\\&=&|1+i|\times\left|z_{n}-1\right|\\&=&\sqrt{2}u_{n} \end{array}$
pour tout entier naturel $n$
b. La distance $BA_{n}$ est égale & $\left|z_{n}-1\right|$ soit $u_{n}$
$\begin{array}{rcl} u_{0}&=&\left|z_{0}-1\right|\\&=&|0-1|\\&=&|-1|\\&=&1 \end{array}$
Pour tout $n$, $u_{n+1}=\sqrt{2}u_{n}$ donc la suite $\left(u_{n}\right)$ est géométrique de premier terme $u_{0}=1$ et de raison $q)\sqrt{2}$ donc, pour tout $n$,
$\begin{array}{rcl} u_{n}&=&u_{o}\times q^{n}\\&=&1\times\left(\sqrt{2}\right)^{n}\\&=&\left(\sqrt{2}\right)^{n} \end{array}$
On cherche $n$ tel que $u_{u}>1000$ donc on résout l'inéquation $\left(\sqrt{2}\right)^{2}>1000$ :
$\begin{array}{rcl} \left(\sqrt{2}\right)^{n}>1000&\Longleftrightarrow&\ln\left(\left(\sqrt{2}\right)^{n}\right)>\ln(1000)\\&\Longleftrightarrow&n\times \ln\left(\sqrt{2}\right)>\ln(1000)\ \&\Longleftrightarrow&n>\dfrac{\ln(1000)}{\ln(\sqrt{2})}\dfrac{\ln(1000)}{\ln(\sqrt{2})}\\&\approx&19.9
\end{array}$
donc la distance $BA_{n}$ est supérieure à $1000$ à partir de $n=20$
3.a. $\begin{array}{rcl} 1+i&=&\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+i\dfrac{\sqrt{2}}{2}\right)\\&=&\sqrt{2}\left(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\right)\\&=&\sqrt{2}\mathrm{e}^{i\dfrac{\pi}{4}} \end{array}$
b. Soit $\mathcal{P}_{n}$ la propriété $z_{n}=1-\left(\sqrt{2}\right)^{n}\mathrm{e}^{i\dfrac{n\pi}{4}}$
$\bullet\ $Initialisation
Pour $n=0$,
$\begin{array}{rcl} z_{n}&=&z_{o}&=&0\\&\text{ et }1-\left(\sqrt{2}\right)^{n}\mathrm{e}^{i\dfrac{n\pi}{4}}\\&=&1-\left(\sqrt{2}\right)^{0}\mathrm{e}^{i\dfrac{0\times \pi}{4}}\\&=&1-1\\&=&0 \end{array}$
Donc la propriété est vraie au rang $0$
$\bullet\ $Hérédité
On suppose la propriété vraie au rang $n\geq 0$, c'est-à-dire
$z_{n}=1-\left(\sqrt{2}\right)^{n}\mathrm{e}^{i\dfrac{n\pi}{4}}$
$\begin{array}{rcl} z_{n+1}&=&(1+i)z_{n}-i\\&=&\sqrt{2}\mathrm{e}^{i\dfrac{\pi}{4}}\times\left(1-\left(\sqrt{2}\right)^{n}\mathrm{e}^{i\dfrac{n\pi}{4}}\right)-i\\&=&\sqrt{2}\mathrm{e}^{i\dfrac{\pi}{4}}-\left(\sqrt{2}\right)^{n+1}\mathrm{e}^{i\dfrac{(n+1)\pi}{4}}-i\\&=&1-i-\left(\sqrt{2}\right)^{n+1}\mathrm{e}^{i\dfrac{(n+1)\pi}{4}}-i\\&=&1-\left(\sqrt{2}\right)^{n+1}\mathrm{e}^{i\dfrac{(n+1)\pi}{4}}
\end{array}$
donc la propriété est vraie au rang $n+1$
$\bullet\ $Conclusion
La propriété est vraie au rang $0$,et elle est héréditaire pour tout $n\geq 0$ ; d'après le
principe de récurrence,elle est vraie pour tout entier naturel $n.$
Donc, pour tout $n$ de $\mathbb{N}$, $z_{n}=1-\left(\sqrt{2}\right)^{n}\mathrm{e}^{i\dfrac{n\pi}{4}}$
c. Le point $A_{2020}$ a pour affixe $z_{2020}=1-\left(\sqrt{2}\right)^{2020}\mathrm{e}^{i\dfrac{2020\pi}{4}}$
$\begin{array}{rcl} \dfrac{2020\pi}{4}&=&505\pi252\times 2\pi+\pi\\&\text{ donc }\mathrm{e}^{i\dfrac{2020\pi}{4}}\\&=&\mathrm{e}^{i\left(252\time 2\pi+\pi\right)}\\&=&\left(\mathrm{e}^{i2\pi}\right)^{252}\times\mathrm{e}^{i\pi}\\&=&1^{252}\times\mathrm{e}^{i\pi}\\&=&-1 \end{array}$
$z_{2020}=1-(\sqrt{2})^{2020}\times(-1)=1+\left(\sqrt{2}\right)^{2020}$ est un réel donc le point $A_{2020}$ appartient à l'axe des abscisses.
Exercice 4
Candidats ayant suivi l'enseignement de spécialité
On considère la matière $M=\begin{pmatrix} 0\quad 1\quad 1\\ 1\quad 0\quad 1\\ 1\quad 1\quad 0
\end{pmatrix}$
Soient $\left(\alpha_{n}\right)$ et $\left(b_{n}\right)$ deux suites tout entier naturel $n$ non nul $\left\lbrace\begin{array}{rcl} a_{n+1}&=&a_{n}+b_{n}\\ b_{n+1}&=&2a_{n} \end{array}\right.$
1.$a_{2}=a_{1}+b_{1}=1+0=1$ ;
$b_{2}=2a_{1}=2\times 1=2$ ;
$a_{3}=a_{2}+b_{2}=1+2=3$ ;
$b_{3}=2\times 1=2$
2. $\begin{array}{rcl} M^{2}&=&\begin{pmatrix} 0\quad 1\quad 1\\ 1\quad 0\quad 1\\ 1\quad 1\quad 0 \end{pmatrix}\times\begin{pmatrix} 0\quad 1\quad 1\\ 1\quad 0\quad 1\\ 1\quad 1\quad 0 \end{pmatrix}\\&=&\begin{pmatrix} 2\quad 1\quad 1\\ 1\quad 2\quad 1\\ 1\quad 1\quad 2
\end{pmatrix} \end{array}$
$\begin{array}{rcl} M^{2}&=&\begin{pmatrix} 2\quad 1\quad 1\\ 1\quad 2\quad 1\\ 1\quad 1\quad 2 \end{pmatrix}\\&=&\begin{pmatrix} 0\quad 1\quad 1\\ 1\quad 0\quad 1\\ 1\quad 1\quad 0 \end{pmatrix}+\begin{pmatrix} 2\quad 0\quad 0\\ 0\quad 2\quad 0\\ 0\quad 0\quad 2 \end{pmatrix}\\&=&\begin{pmatrix} 0\quad 1\quad 1\\ 1\quad 0\quad 1\\ 1\quad 1\quad 0 \end{pmatrix}+2\begin{pmatrix} 1\quad 0\quad 0\\ 0\quad 1\quad 0\\ 0\quad 0\quad 1 \end{pmatrix}\\&=&M+2I \end{array}$
On admet que pour tout entier naturel non nul $n$, $M^{n}=a_{n}M+b_{n}I$, où $\left(a_{n}\right)$ et $\left(b_{n}\right)$ sont les suites précédemment définies.
3. On note $A=\begin{pmatrix} 1\quad 1\\ 2\qu 0 \end{pmatrix}$ et pour tout $n\neq 0$, $X_{n}$ la matrice $\begin{pmatrix} a_{n}\\ b_{n} \end{pmatrix}$
On pose $P=\begin{pmatrix} 1\quad 1\\ 1\quad -2 \end{pmatrix}$
a. $\begin{array}{rcl} AX_{n}&=&\begin{pmatrix} 1\quad 1\\ 2\quad 0 \end{pmatrix}\times\begin{pmatrix} a_{n}\\ b_{n} \end{pmatrix}\\&=&\begin{pmatrix} a_{n}+b_{n}\\ 2an+0 \end{pmatrix}\\&=&\begin{pmatrix} a_{n+1}\\ b_{n+1} \end{pmatrix}\\&=&X_{n+1} \end{array}$
b. On peut dire que $X_{2}=AX_{1}$, $X_{3}=AX_{2}=A\left(AX_{1}\right)=A^{2}X_{1}$ etc..., donc que $X_{n}=A^{n-1}X_{1}$
c. $d$ et $(P)=1\times (-2)-1\times 1=-3\neq 0$ donc la matrice $P$ est inversible.
$\bullet\ \begin{array}{rcl} \begin{pmatrix} 1\quad 1\\ 1\quad -2 \end{pmatrix}\times \begin{pmatrix} \dfrac{2}{3}\quad \dfrac{1}{3}\\ \dfrac{1}{3}\quad -\dfrac{1}{3} \end{pmatrix}\\&=&\begin{pmatrix} \dfrac{2}{3}+\dfrac{1}{3}\quad \dfrac{1}{3}-\dfrac{1}{3}\\ \dfrac{2}{3}-\dfrac{2}{3}\quad \dfrac{1}{3}+\dfrac{2}{3} \end{pmatrix}\\&=&\begin{pmatrix} 1\quad 0\\ 0\quad 1 \end{pmatrix}\\&=&I_{2} \end{array}$
$\bullet\ \begin{array}{rcl} \begin{pmatrix} \dfrac{2}{3}\quad \dfrac{1}{3}\\ \dfrac{1}{3}\quad -\dfrac{1}{3} \end{pmatrix}\times \begin{pmatrix} 1\quad 1\\ 1\quad -2 \end{pmatrix}\\&=&\begin{pmatrix} \dfrac{2}{3}+\dfrac{1}{3}\quad \dfrac{2}{3}-\dfrac{2}{3}\\ \dfrac{1}{3}-\dfrac{1}{3}\quad \dfrac{1}{3}+\dfrac{2}{3} \end{pmatrix}\\&=&\begin{pmatrix} 1\quad 0\\ 0\quad 1 \end{pmatrix}\\&=&I_{2} \end{array}$
Donc l'inverse de la matrice $P$ est la matrice $P^{-1}=\begin{pmatrix} \dfrac{2}{2}\quad \dfrac{1}{3}\\
\dfrac{1}{3}\quad -\dfrac{1}{3} \end{pmatrix}$
d. $\begin{array}{rcl} P^{-1}AB&=&\begin{pmatrix} \dfrac{2}{3}\quad \dfrac{1}{3}\\ \dfrac{1}{3}\quad -\dfrac{1}{3} \end{pmatrix}\times\begin{pmatrix} 1\quad 1\\ 2\quad 0 \end{pmatrix}\times\begin{pmatrix} 1\quad 1\\ 1\quad -2 \end{pmatrix}\\&=&\begin{pmatrix} \dfrac{2}{3}\quad\dfrac{1}{3}\\ \dfrac{1}{3}\quad -\dfrac{1}{3} \end{pmatrix}\times \begin{pmatrix} 1+1\quad 1-2\\ 2+0\quad 2+0 \end{pmatrix}\\&=&\begin{pmatrix} \dfrac{2}{3}\quad \dfrac{1}{3}\\ \dfrac{1}{3}\quad -\dfrac{1}{3} \end{pmatrix}\times\begin{pmatrix}
2\quad -1\\ 2\quad 2 \end{pmatrix}\\&=&\begin{pmatrix} \dfrac{4}{3}+\dfrac{2}{3}-\dfrac{2}{3}+\dfrac{2}{3}\\ \dfrac{2}{3}-\dfrac{2}{3}\quad -\dfrac{1}{3}-\dfrac{2}{3} \end{pmatrix}\\&=&\begin{pmatrix} 2\quad 0\\ 0\quad -1 \end{pmatrix} \end{array} $
qui est une matrice diagonale appelée $D.$
e. Soit $\mathfrak{P}_{n}$ la propriété : $A^{n}=PD^{n}P^{-1}$
$\bullet\ $ Initialisation
$P^{-1}AP=D$ donc $PP^{-1}APP^{-1}=PDP^{-1}$
autrement dit $A=PDP^{-1}$ soit $A^{1}=PD^{1}P^{-1}$
La propriété est vraie au rang $n=1$
Hérédité
On suppose la propriété vraie au rang $n\geq 1$, c'est-à-dire : $A^{n}=PD^{n}P^{-1}$ donc la propriété est vraie au rang $n=1$
$\bullet\ $Conclusion
La propriété est vraie au rang $1$,et elle est héréditaire pour tout $n\geq 1$ ; d'après le
principe de récurrence, elle est vraie pour tout entier naturel $n$
On a donc démontré que,pour tout $n\geq 1$, $A^{n}=PD^{n}P^{-1}$
f. On admet que pour tout $n\geq 1$ : $A^{n-1}X_{1}=\begin{pmatrix} \dfrac{1}{3}\times 2^{n}+\dfrac{1}{3}\times (-1)^{n-1}\quad \dfrac{1}{3}\times 2^{n-1}+\dfrac{1}{3 \times(-1)^{n}\\ \dfrac{1}{3}\times 2^{n}-\dfrac{2}{3}\times(-1)^{n-1}\quad \dfrac{1}{3}\times 2^{n-1}-\dfrac{2}{3}\times (-1)^{n} \end{pmatrix}$
$\begin{array}{rcl} \begin{pmatrix} a_{n}\\ b_{n} \end{pmatrix}&=&X_{n}\\&=&A^{n-1}X_{1}\\&=&\begin{pmatrix}
\dfrac{1}{3}\times 2^{2}+\dfrac{1}{3}\times (-1)^{n-1}\quad \dfrac{1}{3}\times 2^{n-1}+\dfrac{1}{3}\times (-1)^{n}\\ \dfrac{1}{3}\times 2^{n}-\dfrac{2}{3}\times (-1)^{n-1}\quad \dfrac{1}{3}\times 2^{n-1}-\dfrac{2}{3}\times (-1)^{2}\end{matrix}\times \begin{pmatrix} 1\\ 0 \end{pmatrix}\\&=&\begin{pmatrix} \dfrac{1}{3}\times 2^{n}+\dfrac{1}{3}\times (-1)^{n-1}\\ \dfrac{1}{3}\times 2^{n}-\dfrac{2}{3}\times (-1)^{n-1}
\end{pmatrix} \end{array}$
Donc $a_{n}=\dfrac{1}{3}\times 2^{n}+\dfrac{1}{3}\times (-1)^{n-1}=\dfrac{1}{3}\left(2^{n}+(-1)^{n-1}\right)$
4. Soit $k$ un entier naturel
$2^{4}=16\equiv 1^{k}$ modulo $5$, donc $2^{4k}-1\equiv 0$ modulo $5$
5. Soit $n$ un entier naturel non nul et multiple de $4$ ; donc on peut écrire $n=4k$
a. $a_{n}=\dfrac{1}{3}\left(2^{2}+(-1)^{n-1}\right)$ donc
$\begin{array}{rcl} 3a_{n}&=&2^{n}+(-1)^{n-1}\\&=&2^{4k}+(-1)^{4k-1}\\&=&2^{4k}+(-1)^{4k}\times (-1)^{-1}\\&=&2^{4k}-1&\equiv&0 \end{array}$ modulo $5$
Donc $3a_{n}$ est divisible par $5.$
b. $3a_{n}$ est divisible par $5$ donc $5$ divise $3a_{n}$
Or $3$ et $5$ sont premiers entre eux donc, d' après le théorème de Gauss,$5$ divise $a_{n}$,ce qui veut dire que $a_{n}$ est divisible par $5.$

Ajouter un commentaire