Corrigé du baccalauréat S -Nouvelle Calédonie - 2 décembre 2020

1. On considère l'équation $(E)\ :\ z^{3}=4z^{2}-8z+8$ ayant pour inconnue le nombre complexe $z$

a.  $\begin{array}{rcl} (z-2)\left(z^{2}-2z+4\right)&=&z^{3}-2z^{2}+4z-2z^{2}+4z-8\\&=&z^{3}-4z^{2}+8z-8 \end{array}$

b. $\begin{array}{rcl} (E)&\Leftrightarrow&z^{3}-4z^{2}+8z-8=0\\&\Leftrightarrow&(z-2)\left(z^{2}-2z+4\right)=0\\&\Leftrightarrow&z-2=\\&\text{ ou }&z^{2}-2z+4=0 \end{array}$

$\bullet\ z-2=0\Leftrightarrow z=2$

$\bullet\ $On résout $z^{2}-2z+4=0$ ; $\Delta=(-2)^{2}-4\times 1\times 4=-12=-\left(2\sqrt{3}\right)^{2}$

L'équation admet deux solution conjuguées :

$z_{1}=\dfrac{2+i\times 2\sqrt{3}}{2}=1+i\sqrt{3}$ et $z_{2}=1-i\sqrt{3}$

L'ensemble solution de l'équation $(E)$ est : $\left\lbrace 2\ ;\ 1+i\sqrt{3}\ ;\ 1-i\sqrt{3}\right\rbrace$

c. On écrit les solutions de l'équation $(E)$ sous forme exponentielle :

$\bullet\ 2=2\mathrm{e}^{0}$

$\bullet\ 1+i\sqrt{3}=2\left(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)=2\left(\cos\dfrac{\pi}{3}+i\sin \dfrac{\pi}{3}\right)=2\mathrm{e}^{i\dfrac{\pi}{3}}$

$\bullet\ 1-i\sqrt{3}$ est le conjugué de $1+i\sqrt{3}$ donc $1-i\sqrt{3}=2\mathrm{e}^{-i\dfrac{\pi}{3}}$

 On munit le plan complexe d'un repère orthonormé direct $\left(O\ ;\ \vec{u}\;,\vec{v}\right)$

Soit $A$, $B$, $C$ et $D$ les quatre points d'affixes respective

$z_{A}=1+i\sqrt{3}$ $z_{B}=2$ $z_{C}=1-i\sqrt{3}$ $z_{D}=1$

Ces quatre points sont représentés dans la figure ci-dessous

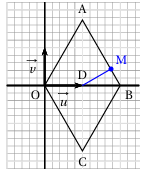
2. $\bullet\ $Le milieu de $[OB]$ a pour affixe $\dfrac{z_{0}+z_{b}}{2}=\dfrac{0+2}{2}=1=z_{D}$

Le milieu de $[AC]$ a pour affixe $\dfrac{z_{A}+z_{C}}{2}=\dfrac{1+i\sqrt{3}+1-i\sqrt{3}}{2}=1=z_{D}$

$\bullet\ $Les segments $[OB]$ et $[AC]$ ont le même milieu $D$ donc $OABC$ est un parallélogramme

$\bullet\ OA=|z_{A}|=\left|1+i\sqrt{3}\right|=|2\mathrm{e}^{i\dfrac{\pi}{3}}|=2$

$\bullet\ OC=\left|z_{C}\right|=\left|1-i\sqrt{3}\right|=\left|2\mathrm{e}^{-i\dfrac{\pi}{3}}\right|=2$

 Le parallélogramme $OABC$ a deux côtés consécutifs de même longueur donc $OABC$ est un losange

3. Soit $M$ le point d'affixe $z_{M}=\dfrac{7}{4}+i\dfrac{\sqrt{3}}{4}$

a. Pour démontrer que les points $A$,$M$ et $B$ sont alignés, on va utiliser les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ :

$\bullet\ \overrightarrow{AM}$ a pour affixe

$\begin{array}{rcl} z_{\overrightarrow{AM}}&=&\dfrac{7}{4}+i\dfrac{\sqrt{3}}{4}-1-i\sqrt{3}\\&=&\dfrac{3}{4}-i\dfrac{3}\\ \end{array}$

$\bullet\ \overrightarrow{AB}$ a pour affixe

$\begin{array}{rcl} z_{\overrightarrow{AB}}&=&2-1-i\sqrt{3}\\&=&1-i\sqrt{3} \end{array}$

$\bullet\ \overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}$ donc les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires

Les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires donc les points $A$, $M$ et $B$ sont alignés.

b. $\bullet\ $ Le vecteur $\overrightarrow{AB}$ a pour affixe $1-i\sqrt{3}$ donc il a pour coordonnées $\left(1\ ;\ -\sqrt{3}\right)$

$\bullet\ $ Le vecteur $\overrightarrow{DM}$ a pour affixe $\dfrac{7}{4}+i\dfrac{\sqrt{3}}{4}-1=\dfrac{3}{4}+i\dfrac{\sqrt{3}}{4}$ donc il a pour coordonnées $\left(\dfrac{3}{4}\ ;\ \dfrac{\sqrt{3}}{4}\right)$

$\bullet\ \overrightarrow{AB}\cdot\overrightarrow{DM}=1\times \dfrac{3}{4}+\left(-\sqrt{3}\right)\times \dfrac{\sqrt{3}}{3}=0$ donc $\overrightarrow{AB}\perp \overrightarrow{DM}$

On en déduit que le triangle $DMB$ est rectangle en $M$

 
Le phaéton à bec rouge est un oiseau des régions intertropicales.
 
1. Lorsque le phaéton à bec rouge vit dans un environnement pollué,sa durée de vie,en an
née,est modélisée par une variable aléatoire $X$ suivant une loi normale d'espérance $\mu$ inconnue et d'écart -type $\sigma=0.95$

a.  On considère la variable aléatoire $Y$ définie par $y=\dfrac{X-\mu}{0.95}$

D'après le cours,on peut dire n que la variable aléatoire $Y$ suit la loi normale centrée
réduite.

b. On sait que $P\left(X\geq 4\right)=0.146$ donc $P\left(X\leq 4\right)=1-0.146=0.854$

$\begin{array}{rcl} X\leq 4&\Longleftrightarrow& X-\mu\leq 4-\mu\\&\Longleftrightarrow&\dfrac{X-\mu}{0.95}\leq \dfrac{4-\mu}{0.95}\\&\Longleftrightarrow& y\leq \dfrac{4-\mu}{0.95} \end{array}$

Donc $P\left(X\leq 4\right)=0.854$ équivaut à $P\left(Y\leq\dfrac{4-\mu}{0.95}\right)=0.854$

On sait que $Y$ suit la loi normale centrée réduite,donc on peut déterminer à la calculatrice le nombre $\alpha$ tel que $P\left(Y\leq \alpha\right)=0.854$ ; on trouve $\alpha\thickapprox 1.0537$

Donc $\mu$ vérifie $\dfrac{4-\mu}{0.9}\thickapprox 1.0537$ ,c'est-à-dire $\mu\thickapprox 4-0.95\times 1.0537$ ce qui donne $\mu\thickapprox 3$

2.Lorsque le phaéton à bec rouge vit dans une environnement sain,sa durée de vie,en année,
est modélisée par une variable aléatoire $Z.$

Les courbes des fonctions de densité associées aux lois de $X$ et de $Z$ sont représentées sur

l'ANNEXE à rendre avec la copie.

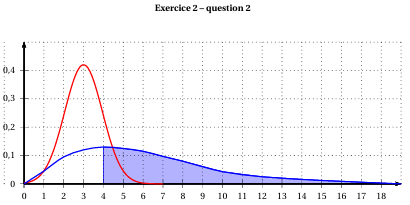
a. La variable aléatoire $X$ suit une loi normale de moyenne $\mu=3$ ; donc la courbe de la fonction de densité associée à $X$ est symétrique par rapport à la droite verticale d'équation $x=3.$

C'est donc la courbe $\mathbb{C_{2}}$

b.Sur l'ANNEXE ,on hachure la zone du plan correspondant à $P\left(Z\geq 4\right)$

On admettra par la suite que $P\left(Z\geq 4\right)=0.677$

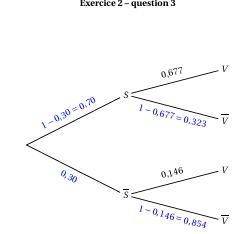
3. Une étude statistique portant sur une région donnée,a permis d'établir que $30\%$ des phaétons à bec rouge vivent dans un environnement pollué;les autres vivent dans un environnement sain.

On choisit au hasard un phaéton à bec rouge vivant dans la région donnée.

On considère les évènements suivants:
 
$\bullet\ S$ :« le phaéton à bec rouge choisi vit dans un environnement sain »;

$\bullet\ V$ :« le phaéton à bec rouge choisi a une durée de vie d'au moins $4$ ans ».

a. On complète l'arbre pondéré illustrant la situation sur l'ANNEXE.

b. D'après la formule des probabilités totales

$\begin{array}{rcl} P(V)&=&P\left(S\cap V\right)\\&=&P\left(\overline{S}\cap V\right)\\&=&0.7\times 0.677+0.3\times 0.146\\&=&0.5177\\&\thickapprox&0.518 \end{array}$$

c. Sachant que le phaéton à bec rouge a une durée de vie d'au moins $4$ ans la probabilité qu'il vive dans un environnement sain est : $\begin{array}{rcl} P_{v}(S)&=&\dfrac{P\left(V\cap S\right)}{P(V)}\\&=&\dfrac{0.7\times 0.677}{0.5177}\\&\thickapprox&0.915 \end{array}$

Soit $g$ la fonction définie sur $\mathbb{R}$, par $g(x)=x^{2}+x+\dfrac{1}{4}+\dfrac{4}{\left(1+\mathrm{e}^{x}\right)^{2}}$

On admet que la fonction $g$ est dérivable sur $\mathbb{R}$ et on note $g'$ sa fonction dérivée.

1. On détermine les limites de $g$ en $+\infty$ en et $-\infty$

$\bullet\ $Limite en $+\infty$

$\lim\limits_{x\longrightarrow\,+\infty}x^{2}+x+\dfrac{1}{4}=\lim\limits_{x\longrightarrow\,+\infty}x^{2}\\=+\infty$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow\,+\infty}\mathrm{e}&=&+ \infty\Rightarrow\lim\limits_{x\longrightarrow\,+\infty}\left(1+\mathrm{e}^{x}\right)^{2}\\&=&+\infty\Rightarrow\lim\limits_{x\longrightarrow\,+\infty}\dfrac{4}{\left(1+\mathrm{e}^{x}\right)^{2}}\\&=&0\\&\text{ Donc }&\lim\limits_{x\longrightarrow\,+\infty}x^{2}+x+\dfrac{1}{4}+\dfrac{4}{\left(1+\mathrm{\mathrm{e}^{x}}\right)}^{2}\\&=&+\infty\;,\\&\text{c'est-à-dire}&\lim\limits_{x\longrightarrow\,+\infty}g(x)\\&=&+\infty \end{array}$

$\bullet\ $Limite en $-\infty$

$\lim\limits_{x\longrightarrow\,-\infty}x^{2}+x+\dfrac{1}{4}=\lim\limits_{x\longrightarrow\,-\infty}x^{2}=+\infty$

$\begin{array}{rcl} \lim\limits_{x\longrightarrow\,-\infty}\mathrm{e}^{x}&=&0\Rightarrow\,\lim\limits_{x\longrightarrow\,-\infty}\left(1+\mathrm{e}^{x}\right)\\&=&1\Rightarrow\,\lim\limits\dfrac{4}{\left(1+\mathrm{e}^{x}\right)^{2}}=4\\&\text{Donc }&\lim\limits_{x\longrightarrow\,-\infty}x^{2}+x+\dfrac{1}{4}+\dfrac{4}{\left(1+\mathrm{e}^{x}\right)^{2}}\\&=&+\infty\;,\\&\text{c'est-à-dire }&g(x)\\&=&+\infty \end{array}$

2. On admet que la fonction $g'$ est strictement croissante sur $\mathbb{R}$ et que $g'(0)=0$

$\bullet\ $ Pour $x<0$, comme la fonction $g'$ est strictement croissante,on a $g'(x)<g'(0)$ ; on sait que $g'(0)=0$ donc,pour tout $x<0$,on a $g'(x)<0$

$\bullet\ $Pour $x<0$, comme la fonction $g'$ est strictement croissante,on a $g'(x)<g'(0)$;on sait que $g'(0)=0$ donc,pour tout $x>0$,on a $g'(x)>0$

3. La fonction $g'$ s'annule et change de signe pour $x=0$ ; elle passe de négative à positive, donc la fonction $g$ admet un minimum en $x=0$ qui vaut $g(0)=\dfrac{1}{4}+\dfrac{4}{(1+1)^{2}}=\dfrac{5}{4}$

On dresse le tableau des variations de la fonction $g$ :

$\begin{array}{|c|ccccc|} \hline x&-\infty&&0&&+\infty\\ \hline g'(x)&&-&\vert&+&\\ \hline &+\infty&\searrow&&\nearrow&+\infty\\ g&&&\dfrac{5}{4}&&\\ \hline \end{array}$

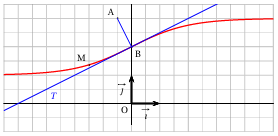
Soit $f$ la fonction définie sur $\mathbb{R}$ par : $f(x)=3-\dfrac{2}{1+\mathrm{e}^{x}}$

On désigne par $\mathbb{C}_{f}$ la courbe représentative de $f$ dans un repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\right)$, représenté dans la figure ci-dessous

Soit $A$ le point de coordonnées $\left(-\dfrac{1}{2}\ ;\ 3\right)$

1. $f(0)=3-\dfrac{2}{1+\mathrm{e}^{0}}=3-\dfrac{2}{2}=2$ donc le point $B(0\ ;\ 2)$ appartient à $\mathbb{C}_{f}$

2. Soit $x$ un réel quelconque

On note $M$ le point de la courbe $\mathbb{C}_{f}$ de coordonnées $(x\ ;\ f(x))$

$\begin{array}{rcl}AM^{2}&=&\left(x_{M}-x_{A}\right)^{2}+\left(y_{M}-y_{A}\right)^{2}\\&=&\left(x-\left(-\dfrac{1}{2}\right)\right)^{2}+(f(x)-3)^{2}\\&=&\left(x+\dfrac{1}{2}\right)^{2}+\left(3-\dfrac{2}{1+\mathrm{e}^{x}-3}\right)^{2}\\&=&x^{2}+x+\dfrac{1}{4}+\left(-\dfrac{2}{1+\mathrm{e}^{x}}\right)^{2}\\&=&x^{2}+x+\dfrac{1}{4}+\dfrac{4}{\left(x+\mathrm{e}^{2}\right)}\\&=&g(x) \end{array}$

3. On admet que la distance $AM$ est minimale si et seulement si $AM^{2}$ est minimal.

$AM^{2}=g(x)$ et $g(x)$ est minimale pour $x=0$ ; $AM$ est minimale pour $x=0$ donc si $M$ a pour abscisse $0$, c'est-à-dire est en $B$

4. On admet que la fonction $f$ est dérivable sur $R$ et on note $f'$ sa fonction dérivée.

a. Pour tout réel $\begin{array}{rcl} x\;,f'(x)&=&0-\dfrac{0-2\mathrm{e}^{x}}{\left(1+\mathrm{e}^{x}\right)^{2}} \end{array}$

b. Soit $T$ la tangente à la courbe $\mathbb{C}_{f}$ au point $B$

L'équation réduite de $T$ est : $y=f'(0)(x-0)+f(0)$

$\bullet\ \begin{array}{rcl} f'(x)&=&\\&=&\dfrac{2\mathrm{e}^{x}}{\left(1+\mathrm{e}^{2}\right)^{2}}\\&\text{ donc }f'(0)\\&=&\dfrac{2\times 1}{(1+1)^{2}}\\&=&\dfrac{1}{2}\end{array}$

$\bullet\ \begin{array}{rcl} f(0)=yB=2 \end{array}$

Donc l'équation réduite de $T$ est $y=\dfrac{x}{2}+2$

5. La droite $T$ a pour équation $y=\dfrac{x}{2}+2$ soit $\dfrac{x}{2}-y+2=0$ ; elle a donc pour vecteur normal $\vec{n}\left(\dfrac{1}{2}\ ;\ -1\right)$

le vecteur $\overrightarrow{AB}$ a pour coordonnées $\left(0-\left(-\dfrac{1}{2}\right)\ ;\ 2-3\right)$ soit $\left(\dfrac{1}{2}\ ;\ -1\right)$ ; il est donc normal à la droite $T$

On en déduit que la droite $T$ est perpendiculaire à la droite $(AB)$

Candidats n'ayant pas suivi l'enseignement de spécialité

1. Affirmation 1 : L'équation $\left(3\ln x-5\right)\left(\mathrm{e}^{x}+4\right)=0$ admet exactement deux solutions réelles

$\begin{array}{rcl} \left(3\ln x-5\right)\left(\mathrm{e}^{x}+4\right)&=&0\Longleftrightarrow\,3\ln x-5\\&=&0\\&\text{ ou }&\mathrm{e}^{x}+4\\&=&0 \end{array}$

$\bullet\ 3\ln x-5=0\Longleftrightarrow\ln x=\dfrac{5}{3}\Longleftrightarrow x=\mathrm{e}^{\dfrac{5}{3}}$ ; une solution réelle

$\bullet\ \mathrm{e}^{x}+4=0$ n'a pas de solution réelle car $\mathrm{e}^{x}>0\Rightarrow\mathrm{e}^{x}>4>0$ pour tout $x.$

L'équation n'a donc qu'une solution réelle.

Affirmation 1 fausse

2. On considère la suite $\left(u_{n}\right)$ définie par $u_{0}=2$ et, pour tout $n$, $u_{n+1}=2u_{n}-5n+6$

Affirmation 2 : Pour tout entier naturel $n$, $u_{n}=3\times 2^{n}+5n-1$

En calculant quelques termes de la suite, $2$, $10$, $21$, $38$, $67$, $120$, on peut conjecturer que la propriété $u_{n}=3\times 2^{n}+5n-1$ est vraie, pour tout $n$

On va démontrer cette propriété par récurrence

$\bullet\ $Initialisation

Pour $n=0$, on a $u_{0}=2$ et $3\times 2^{n}+5n-1=3\times 1+0-1=2$

Donc la propriété est vraie pour $n=0$

$\bullet\ $Hérédité

On suppose la propriété vraie au rang $n\geq 0$ ; c'est-à-dire : $u_{n}=3\times 2^{n}+5n-1$

On veut démontrer que $u_{n+1}=3\times 2^{n+1}+5(n+1)-1$

$\begin{array}{rcl} u_{n+1}&=&2u_{n}-5n+6\\&=&2\left(3\times 2^{n}+5n-1\right)-5n+6\\&=&3\times 2^{n+1}+10n-2-5n+6\\&=&3\times 2^{n+1}+5n+4\\&=&3\times 2^{n+1}+5(n+1)-1 \end{array}$

Donc la propriété est vraie au rang $n+1$
 
$\bullet\ $Conclusion

La propriété est vraie au rang $0$ et elle est héréditaire pour tout $n<0$ ; d'après le principe de récurrence,la propriété est vraie pour tout $n>0$

Affirmation $2$ vrai

3. On considère la suite $\left(u_{n}\right)$ définie, pour tout entier naturel $n$, par $u_{n}=n^{2}+\dfrac{1}{2}$

Affirmation $3$ : La suite $\left(u_{n}\right)$ est géométrique.

On calcule quelques termes de la suite $\left(u_{n}\right)$

$u_{0}=0+\dfrac{1}{2}=\dfrac{1}{2}$ ;

$u_{1}=1^{2}+\dfrac{1}{2}=\dfrac{3}{2}$ ;

$u_{2}=2^{2}+\dfrac{1}{2}=\dfrac{9}{2}$ ;

$u_{3}=3^{2}+\dfrac{1}{2}=\dfrac{19}{2}$ ;

$\dfrac{u_{3}}{u_{2}}=\dfrac{\dfrac{19}{2}}{\dfrac{9}{2}}=\dfrac{19}{9}$ ;

$\dfrac{u_{2}}{u_{1}}=\dfrac{\dfrac{9}{2}}{\dfrac{3}{2}}=\dfrac{9}{3}=3$

$\dfrac{19}{9}\neq 3$ donc la suite $\left(u_{n}\right)$ n'est pas géométrique.

Affirmation $3$ fausse

4. Dans un repère de l'espace, soit $d$ la droite passant par le point $A(-3\ ;\ 7\ ;\ -12)$ et de vecteur directeur $\vec{u}(1\ ;\ -2\ ;\ 5)$

Soit $d'$ la droite ayant pour représentation paramétrique $\left\lbrace\begin{array}{rcl} x&=&2t-1\\ y&=&-4t+3\;,t\in\mathbb{R}\\ z&=&10t-2 \end{array}\right.$

Affirmation $4$ : Les droites $d$ et $d'$ sont confondues.

Les droites sont confondues si elles ont des vecteurs directeurs colinéaires et si elle ont un point en commun.

$\bullet\ $La droite $d'$ a pour vecteur directeur $(2\ ;\ -4\ ;\ 10)$ qui est égal à $2.\vec{u}$ ; les droites $d$ et $d'$ sont donc parallèles.
 
$\bullet\ $ On regarde si le point $A$ appartient à la droite $d'$,autrement dit s'il existe un réel

$t$ tel que : $\left\lbrace\begin{array}{rcl} -3&=&2t-1\\ 7&=&-4t+3\\ -12&=&10t-2 \end{array}\right.$

La valeur $t=-1$ convient donc $A\in d'$

Les deux droites $d$ et $d'$ sont confondues

Affirmation $4$ vraie

5. On considère un cube $ABCDEFGH$ ,L'espace est muni du repère orthonormé $\left(A\ ;\ \overrightarrow{AB}\;,\overrightarrow{AD}\;,\overrightarrow{AE}\right)$

Une représentation paramétrique de la droite $(AG)$ est

$\left\lbrace\begin{array}{rcl} x&=&t\\ y&=&t\quad t\in\mathbb{R}\\ z&=&t \end{array}\right.$

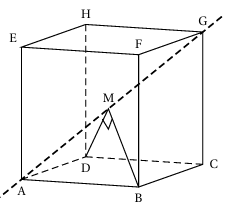
Affirmation $5$ : Il y a exactement deux positions du point $M$ sur la droite $(AG)$ telles que les droites $(MB)$ et $(MD)$ soient orthogonales.

On cherche le point $M$ de $(AG)$ tel que $\overrightarrow{MB}\perp \overrightarrow{MD}$, c'est-à-dire tel que $\overrightarrow{MB}.\overrightarrow{MD}=0$

$\bullet\ M\in(AG)$ donc les coordonnées de $M$ sont de la forme $(t\ ;\ t\ ;\ t)$

$\bullet\ B$ a pour coordonnées $(1\ ;\ 0\ ;\ 0)$ donc $\overrightarrow{MB}$ a pour coordonnées $(1-t\ ;\ -t\ ;\ -t)$

$\bullet\ D$ a pour coordonnées $(0\ ;\ 1\ ;\ 0)$ donc $\overrightarrow{MD}$ a pour coordonnées $(-t\ ;\ 1-t\ ;\ -t)$

$\bullet\ $ $\begin{array}{rcl} \overrightarrow{MB}\cdot\overrightarrow{MD}&=&-t(1-t)+(1-t)(-t)+(-t)(-t)\\&=&-t+t^{2}-t+t^{2}+t^{2}\\&=&3t^{2}-2t\\&=&t(3t-2) \end{array}$

$\bullet\ $ $\begin{array}{rcl} \overrightarrow{MB}\cdot\overrightarrow{MD}&=&0\Longleftrightarrow\,t(3t-2)\\&=&0\Longleftrightarrow\,t\\&=&0\\&\text{ ou }&t\\&=&\dfrac{2}{3} \end{array}$

Il y a exactement deux positions du point $M$ sur la droite $(AG)$ telles que les droites
$(MB)$ et $(MD)$ soient orthogonales; soit $M$ est en $A$ $\text{(pour }t=0)$, soit $M$ a pour coordonnées $\left(\dfrac{2}{3}\ ;\ \dfrac{2}{3}\ ;\ \dfrac{2}{3}\right)$

Affirmation $5$ vraie

Candidats ayant suivi l'enseignement de spécialité

1. Affirmation $1$ : Les solutions de l'équation $7x-12y$, où $x$ et $y$ sont des entiers relatifs,sont les couples $(-1+12k\ ;\ -1+7k)$ où k décrit l'ensemble des entiers relatifs.
 
Les nombres $7$ et $12$ sont premiers entre eux donc, d'après le théorème de Bézout, l'équation$7x-12y=1$ admet des solutions donc l'équation $7x-12y=5$ aussi.

On appelle $(E)$ l'équation $7x-12y=5$

$\bullet\ $Pour tout entier relatif $k$, si $x=-1+12k$ et $y=-1+7k$, alors

$\begin{array}{rcl} 7x-12y&=&7(-1+12k)-12(-1+7k)\\&=&-7+84k+12-84k\\&=&5 \end{array}$, donc le couple

$\bullet\ $On suppose maintenant que le couple $(x\ ;\ y)$ est solution de $(E).$

On sait aussi que $(-1\ ;\ -1)$ est solution de $(E).$

On a donc :

$\dfrac{7x-12y=5\\ 7(-1)-12(-1)=5}{7(x+1)-12(y+1)=0}$ par soustraction membre à membre

Donc $7(x-1)-12(y+1)=0$ ce qui équivaut à $7(x+1)=12(y+1)$

$7((x+1)=12(y+1)$ donc $7$ divise $12(y+1)$ ; or $7$ et $12$ sont premiers entre eux, donc, d'après le théorème de Gauss, $7$ divise $y+1$

On peut donc écrire $y+1$ sous la forme $7k$ donc $y=-1+7k$

$7(x+1)=12(y+1)$ et $y+1=7k$ donc $7(x+1)=12\times 7k$ donc $x+1=12k$ ce qui veut dire que $x=-1+12k$

Donc les solutions de l'équation $7x-12y=5$, où $x$ et $y$ sont des entiers relatifs, sont les couples $(-1+12k\ ;\ -1+7k)$ où $k$ décrit l'ensemble des entiers relatifs.

Affirmation 1 vraie

2. Affirmation 2 : Pour tout entier naturel $n$ le reste de la division euclidienne de $4+3\times 15^{n}\equiv 1$

$(\text{mod }3)$

Comme $0\leq 1<3$, on peut dire que pour tout $n$, le nombre $1$ est le reste de la division

de $4+3\times 15^{n}$ par $3$

Affirmation 2 vraie

Affirmation 3 : l'équation $n\left(2n^{2}+3n+5\right)=3$, où $n$ est un entier naturel, admet au moins une solution

On a $n\left(2n^{2}+3n+5\right)=3$, où $n$ entier naturel ; donc $n$ divise $3$, donc $n=1$ ou $n=3$

$\bullet\ $Si $n=1$, on a $n\left(2n^{2}-3n+5\right)=1(2-3+5)=4\neq 3$

$\bullet\ $Si $n=3$, on a $n\left(2n^{2}-3n+5\right)=3(18-9+5)=42\neq 3$

L'équation n'a pas de solution

Affirmation 3 fausse

4. Soit $t$ un nombre réel.

On pose $A=\begin{pmatrix} t\quad 3\\ 2t\quad -t \end{pmatrix}$

Affirmation 4 : Il n'existe aucune valeur du réel $t$ pour laquelle $A^{2}=\begin{pmatrix} 1\quad 0\\ 0\quad 1 \end{pmatrix}$

$\begin{array}{rcl} A^{2}&=&\begin{pmatrix} t\quad 3\\ 2t\quad -t \end{pmatrix}\begin{pmatrix} t\quad 3\\ 2t\quad -t \end{pmatrix}\\&=&\begin{pmatrix} t^{2}+6t\quad 3t-3t\\ 2t^{2}-2t^{2}\quad 6t+t^{2} \end{pmatrix}\\&=&\begin{pmatrix} t^{2}+6t\quad 0\\ 0\quad t^{2}+6t \end{pmatrix} \end{array}$
 
$\begin{array}{rcl} A^{2}&=&\begin{pmatrix} 1\quad 0\\ 0\quad 1 \end{pmatrix}\\&\Longleftrightarrow&t^{2}+6t\\&=& \end{array}$

$t^{2}+6t=1\Longleftrightarrow t^{2}+6t-1=0$ ;

$\Delta=6^{2}-4\times 1\times (-1)=40>0$ donc l'équation admet deux solution distinctes ; il y a donc deux valeurs de $t$ pour lesquelles $A^{2}=\begin{pmatrix} 1\quad 0\\ 0\quad 1 \end{pmatrix}$

Ce sont $-3+\sqrt{10}$ et $-3-\sqrt{10}$

Affirmation 4 fausse

5. On considère les matrices $A=\begin{pmatrix} 0\quad 1\quad -1\\ -1\quad 2\quad -1\\ 1\quad -1\quad 2 \end{pmatrix}$ et $I_{3}\begin{pmatrix} 1\quad 0\quad 0\\ 0\quad 1\quad 0\\ 0\quad 0\quad 1 \end{pmatrix}$

Affirmation 5 : Pour tout entier $n\geq 2$, $A^{n}=\left(2^{n}-1\right)A+\left(2-2^{n}\right)I_{3}$

On va démontrer par récurrence que la propriété $A^{n}=\left(2^{n}-1\right)A+\left(2-2^{2}\right)I_{3}$ est vraie pour tout $n\geq 2$

$\bullet\ $Initialisation

Pour $n=2$, $\begin{array}{rcl} A^{2}&=&\begin{pmatrix} 0\quad 1\quad -1\\ -1\quad 2\quad -1\\ 1\quad -1\quad 2 \end{pmatrix}\begin{pmatrix} 0\quad 1\quad -1\\ -1\quad 2\quad -1\\ 1\quad -1\quad 2 \end{pmatrix}\\&=&\begin{pmatrix} -2\quad 3\quad -3\\ -3\quad 4\quad -3\\ 3\quad -3\quad 4 \end{pmatrix} \end{array}$

$\left(2^{n-1}\right)A+\left(2-2^{n}\right)I_{3}$ devient

$\begin{array}{rcl} 3A-2I_{3}&=& \begin{pmatrix} 0\quad 3\quad -3\\ -3\quad 6\quad -3\\ 3\quad -3\quad 6 \end{pmatrix}-\begin{pmatrix} 2\quad 0\quad 0\\ 0\quad 2\quad 0\\ 0\quad 0\quad 2 \end{pmatrix}\\&=&\begin{pmatrix} -2\quad 3\quad -3\\ -3\quad 4\quad -3\\ 3\quad -3\quad 4 \end{pmatrix}\\&=&A^{2}\end{array}$

La propriété est donc vérifiée pour $n=2$

$\bullet\ $Hérédité

On suppose la  propriété vraie pour le rang $n\geq 2$ et on va démontrer qu'elle est
vraie pour le rang $n+1$

Autrement dit,on suppose $A^{n}=\left(2^{n}-1\right)A+\left(2-2^{n}\right)I_{3}$ et on veut démontrer

$A^{n+1}=\left(2^{n+1}-1\right)A+\left(2-2^{n+1}\right)I_{3}$

$\begin{array}{rcl} A^{n+1}&=&A^{n}\times A\\&=&\left(\left(2^{n}-1\right)A+\left(2-2^{n}\right)I_{3}\right)\times A&=&\left(2^{n}-1\right)A^{2}+\left(2-2^{2}\right)A\\ &=&\left(2^{n}-1\right)\left(3A-2I_{3}\right)+2A-2n^{n}A&=&3\times 2^{n}A-3A-2^{n}\times 2I_{3}+2I_{3}+2A-2^{n}A\\&=& 2\times 2^{n}A-A+2I_{3}-2^{n+1}I_{3}&=&2^{n+1}A-A+2I_{3}-2^{n+1}I_{3}\\&=&\left(2^{n+1}-1\right)A+\left(2-2^{n+1}\right)I_{3} \end{array}$

La propriété est donc vraie au rang $n+1$

$\bullet\ $Conclusion

La propriété est vraie au rang $2$ et elle est héréditaire pour tout $n\geq 2$ ; d'après le
principe de récurrence, la propriété est vraie pour tout $n\geq 2$

Affirmation $5$ vraie