Corrigé Bac Maths S2, S2A, S4, S5, 1er groupe 2009
Classe:
Terminale
Exercice 1
1) $(D_{1})$ droite de régression de $Y$ en $X$ ayant pour équation : $y=ax+b$, on a :
$$a=\dfrac{cov(X\;,\ Y)}{V(X)}\quad\text{et}\quad b=\bar{y}-a\bar{x}$$
$(D_{2})$ droite de régression de $X$ en $Y$ ayant pour équation : $x=a'y+b'$, on a :
$$a'=\dfrac{cov(Y\;,\ X)}{V(Y)}\quad\text{et}\quad b'=\bar{x}-a'\bar{y}$$
On en déduit que :
$\begin{array}{rcl} aa'&=&\dfrac{cov(X\;,\ Y)}{V(X)}\dfrac{cov(Y\;,\ X)}{V(Y)}\\ \\&=&\dfrac{\left(cov(X\;,\ Y)\right)^{2}}{V(X)V(Y)}\\ \\&=&\left(\dfrac{cov(X\;,\ Y)}{\sigma(X)\sigma(Y)}\right)^{2}\\ \\&=&r^{2}\end{array}$
D'où, $\boxed{aa'=r^{2}}$
2) $(D_{1})$ droite de régression de $Y$ en $X$ ayant pour équation réduite : $y=2.4x$, on a :
$$a=2.4\quad\text{et}\quad b=0$$
$(D_{2})$ droite de régression de $X$ en $Y$ ayant pour équation réduite : $x=\dfrac{3.5}{9}y+\dfrac{24}{9}$, on a :
$$a'=\dfrac{3.5}{9}\quad\text{et}\quad b'=\dfrac{24}{9}$$
D'après la question précédente, le coefficient de corrélation vérifie :
$\begin{array}{rcl} r^{2}&=&aa'\\ \\&=&2.4\dfrac{3.5}{9}\\ \\&=&\dfrac{14}{15}\end{array}$
Puisque $r=\dfrac{cov(X\;,\ Y)}{\sigma(X)\sigma(Y)}$, que $\sigma(X)\ $ et $\ \sigma(Y)$ sont positifs par définition et que $cov(X\;,\ Y)$ est positif par hypothèse alors, $r$ est positif.
Donc, $\boxed{r=\sqrt{\dfrac{14}{15}}}$
3) On a :
$$\left\lbrace\begin{array}{rcl} -a\bar{x}+\bar{y}&=&b\qquad(1)\\ \bar{x}-a'\bar{y}&=&b'\qquad(2)\end{array}\right.$$
Je garde l'équation 1. Je multiplie l'équation 2 par $a$ pour éliminer $\bar{x}$
$$\left\lbrace\begin{array}{rcl} -a\bar{x}+\bar{y}&=&b\\ a\bar{x}-aa'\bar{y}&=&ab'\end{array}\right.$$
J'additionne membre à membre : $(1-aa')\bar{y}=b+ab'$, c'est à dire
$$\bar{y}=\dfrac{b+ab'}{1-r^{2}}$$
Pour trouver $\bar{x}$ j'utilise l'équation la plus simple ; ici c'est la 2 : $\bar{x}=b'+a'\bar{y}$ ; c'est à dire
$\begin{array}{rcl}\bar{x}&=&b'+a'\dfrac{b+ab'}{1-r^{2}}\\ \\&=&\dfrac{b'-r^{2}b'+a'b+a'ab'}{1-r^{2}}\\ \\&=&\dfrac{b'+a'b}{1-r^{2}}\end{array}$
Donc, $$\bar{x}=\dfrac{b'+a'b}{1-r^{2}}$$
Application numérique : Comme $\dfrac{1}{1-r^{2}}=15$, on a :
$$\bar{y}=15\times 2.4\times\dfrac{24}{9}\quad\text{et}\quad\bar{x}=15\times\dfrac{24}{9}$$
Donc, $\boxed{\bar{y}=96\quad\text{et}\quad\bar{x}=40}$
Exercice 2
1) Pour que $M$ appartiennent à l'axe des abscisses, il faut et il suffit que la partie imaginaire de $z$ soit nulle ; c'est à dire $\ln y=0\ $ ou $\ y=1.$ Donc,
$\begin{array}{rcl} p(A)&=&p(y=0)\\ \\&=&\dfrac{4}{12}\\ \\&=&\dfrac{1}{3}\end{array}$
D'où :
$$\boxed{p(A)=\dfrac{1}{3}}$$
Pour que $M$ appartiennent à l'axe des ordonnées, il faut et il suffit que la partie réelle de $z$ soit nulle ; c'est `a dire $\ln x=0\ $ ou $\ x=1.$ Donc,
$\begin{array}{rcl} p(B)&=&p(x=0)\\ \\&=&\dfrac{4}{12}\\ \\&=&\dfrac{1}{3}\end{array}$
Ainsi,
$$\boxed{p(B)=\dfrac{1}{3}}$$
L'événement contraire de $C$ est $"M$ appartient à au moins un des axes" c'est à dire $A\cup B.$
L'événement $A\cap B$ est $"M$ appartient à chacun des axes" c'est à dire $z=0\ $ ou $\ \ln x=0\ $ et $\ \ln y=0$ finalement $x=y=1.$
Puisque le tirage est avec remise, les événements $A\ $ et $\ B$ sont indépendants, donc :
$$p(A\cap B)=p(A)p(B)=\dfrac{1}{9}$$
Par conséquent :
$\begin{array}{rcl} p(\overline{C})&=&p(A\cup B)\\ \\&=&p(A)+p(B)-p(A\cap B)\\ \\&=&\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{9}\\ \\&=&\dfrac{5}{9}\end{array}$
Ainsi,
$\begin{array}{rcl} p(C)&=&1-p(\overline{C})\\ \\&=&1-\dfrac{5}{9}\\ \\&=&\dfrac{4}{9}\end{array}$
D'où :
$$\boxed{p(C)=\dfrac{4}{9}}$$
Pour que l'angle $(\overrightarrow{OM}\;,\ \vec{i})$ soit égal à $-\dfrac{\pi}{4}$ il faut et il suffit que les coordonnées de $M$ soient égales et strictement positives c'est à dire $\ln x=\ln y>0\ $ ou $\ x=y=\mathrm{e}.$
Par conséquent, $D$ est l'événement $"x=y=\mathrm{e}".$
$\begin{array}{rcl} p(x=\mathrm{e})&=&p(y=\mathrm{e})\\ \\&=&\dfrac{2}{12}\\ \\&=&\dfrac{1}{6}\end{array}$
D'où :
$$\boxed{p(D)=\dfrac{1}{6}\times\dfrac{1}{6}=\dfrac{1}{36}}$$
Pour que $M$ appartienne au cercle trigonométrique, il faut et il suffit que $OM=1$ ; c'est à dire $(\ln x)^{2}+(\ln y)^{2}=1.$
Puisque $x\ $ et $\ y$ ne prennent que les valeurs $1\;,\ \mathrm{e}\ $ et $\ \dfrac{1}{\mathrm{e}}$, $\ln x\ $ et $\ \ln y$ ne prennent que les valeurs $0\;,\ 1\ $ et $\ -1.$
Les seuls couples possibles pour réaliser $(\ln x)^{2}+(\ln y)^{2}=1$ sont donc :
$$(\ln x\;,\ \ln y)=(1\;,\ 0)\;;\ (-1\;,\ 0)\;;\ (0\;,\ 1)\ \text{ ou }\ (0\;,\ -1)$$
c'est à dire
$$(x\;,\ y)=(\mathrm{e}\;,\ 1)\;;\ \left(\dfrac{1}{\mathrm{e}}\;,\ 1\right)\;;\ (1\;,\ \mathrm{e})\ \text{ ou }\ \left(1\;,\ \dfrac{1}{\mathrm{e}}\right)$$
Or,
$\begin{array}{rcl} p((x\;,\ y)=(\mathrm{e}\;,\ 1))&=&p((x\;,\ y)=(1\;,\ \mathrm{e}))\\ \\&=&\dfrac{2}{12}\times\dfrac{4}{12}\\ \\&=&\dfrac{1}{18}\end{array}$
$\begin{array}{rcl} p\left((x\;,\ y)=\left(\dfrac{1}{\mathrm{e}}\;,\ 1\right)\right)&=&p\left((x\;,\ y)=\left(1\;,\ \dfrac{1}{\mathrm{e}}\right)\right)\\ \\&=&\dfrac{6}{12}\times\dfrac{4}{12}\\ \\&=&\dfrac{1}{6}\end{array}$
Donc,
$$\boxed{p(E)=\dfrac{1}{18}+\dfrac{1}{18}+\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{4}{9}}$$
2) a) Puisque $x\ $ et $\ y$ ne prennent que les valeurs $1\;,\ \mathrm{e}\ $ et $\ \dfrac{1}{\mathrm{e}}$, $\ln x\ $ et $\ \ln y$ ne prennent que les valeurs $0\;,\ 1\ $ et $\ -1.$
Les couples de coordonnées possibles sont donc :
$$(0\;,\ 0)\;,\ (0\;,\ 1)\;,\ (0\;,\ -1)\;,\ (1\;,\ 0)\;,\ (1\;,\ 1)$$
$$(1\;,\ -1)\;,\ (-1\;,\ 0)\;,\ (-1\;,\ 1)\;,\ (-1\;,\ -1)$$
correspondant aux valeurs suivantes du couples $(x\;,\ y)\ :$
$$(1\;,\ 1)\;,\ (1\;,\ \mathrm{e})\;,\ \left(1\;,\ \dfrac{1}{\mathrm{e}}\right)\;,\ (\mathrm{e}\;,\ 1)\;,\ (\mathrm{e}\;,\ \mathrm{e})$$
$$\left(\mathrm{e}\;,\ \dfrac{1}{\mathrm{e}}\right)\;,\ \left(\dfrac{1}{\mathrm{e}}\;,\ 1\right)\;,\ \left(\dfrac{1}{\mathrm{e}}\;,\ \mathrm{e}\right)\;,\ \left(\dfrac{1}{\mathrm{e}}\;,\ \dfrac{1}{\mathrm{e}}\right)$$
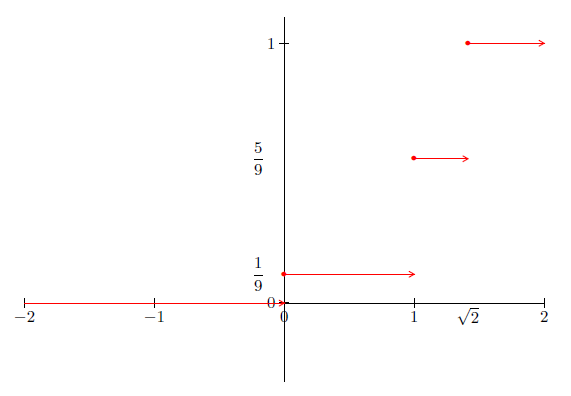
Les distances $OM$ possibles sont donc : $0\;,\ 1\;,\ \sqrt{2}.$
La variable aléatoire $X$ prend les valeurs $0\;,\ 1\;,\ \sqrt{2}.$
$\begin{array}{rcl} p(X=0)&=&p((x\;,\ y)=(1\;,\ 1))\\ \\&=&\dfrac{4}{12}\times\dfrac{4}{12}\\ \\&=&\dfrac{1}{9}\end{array}$
$\begin{array}{rcl} p(X=1)&=&p((x\;,\ y)=(1\;,\ \mathrm{e}))+p((x\;,\ y)=(\mathrm{e}\;,\ 1))\\ \\&&+\ p\left((x\;,\ y)=\left(1\;,\ \dfrac{1}{\mathrm{e}}\right)\right)+p\left((x\;,\ y)=\left(\dfrac{1}{\mathrm{e}}\;,\ 1\right)\right)\\ \\&=&\dfrac{2}{12}\times\dfrac{4}{12}+\dfrac{2}{12}\times\dfrac{4}{12}+\dfrac{4}{12}\times\dfrac{6}{12}+\dfrac{4}{12}\times\dfrac{6}{12}\\ \\&=&\dfrac{4}{9}\end{array}$
$\begin{array}{rcl} p(X=\sqrt{2})&=&p((x\;,\ y)=(\mathrm{e}\;,\ \mathrm{e}))+p\left((x\;,\ y)=\left(\mathrm{e}\;,\ \dfrac{1}{\mathrm{e}}\right)\right)\\ \\&&+\ p\left((x\;,\ y)=\left(\dfrac{1}{\mathrm{e}}\;,\ \mathrm{e}\right)\right)+p\left((x\;,\ y)=\left(\dfrac{1}{e}\;,\ \dfrac{1}{\mathrm{e}}\right)\right)\\ \\&=&\dfrac{2}{12}\times\dfrac{4}{12}+\dfrac{2}{12}\times\dfrac{6}{12}+\dfrac{2}{12}\times\dfrac{6}{12}+\dfrac{6}{12}\times\dfrac{6}{12}\\ \\&=&\dfrac{4}{9}\end{array}$
En résumé :
$$\boxed{p(X=0)=\dfrac{1}{9}\;,\ p(X=1)=\dfrac{4}{9}\;,\ p(X=\sqrt{2})=\dfrac{4}{9}}$$
b) La fonction de répartition de $X$ est définie par :
$$F(x)=p(X<x)$$
Donc,
$-\ $ Si $x\leq 0$ alors, $F(x)=p(X<x)=0$
$-\ $ Si $0<x\leq 1$ alors,
$\begin{array}{rcl} F(x)&=&p(X<x)\\ \\&=&p(X=0)\\ \\&=&\dfrac{1}{9}\end{array}$
$-\ $ Si $1<x\leq\sqrt{2}$ alors,
$\begin{array}{rcl} F(x)&=&p(X<x)\\ \\&=&p(X=0)+p(X=1)\\ \\&=&\dfrac{1}{9}+\dfrac{4}{9}\\ \\&=&\dfrac{5}{9}\end{array}$
$-\ $ Si $\sqrt{2}<x$ alors,
$\begin{array}{rcl} F(x)&=&p(X<x)\\ \\&=&p(X=0)+p(X=1)+p(X=\sqrt{2})\\ \\&=&\dfrac{1}{9}+\dfrac{4}{9}+\dfrac{4}{9}\\ \\&=&1\end{array}$
Exercice 3
L'équation caractéristique associée à $(E)$ est :
$$(E_{c})\ :\ r^{2}+2r+1=0$$
c'est à dire $(r+1)^{2}=0.$
1) Elle a une racine double égale à $-1.$ Par conséquent la solution générale de $(E)$ est :
$$f(x)=(ax+b)\mathrm{e}^{-x}\;;\ a\ \text{ et }\ b \text{ réels arbitraires}$$
2) Pour que la fonction $h\ :\ x\mapsto ax+b$ soit solution de $(E')$ il faut et il suffit que
$$h''(x)+2h'(x)+h(x)=x+3\quad (1)$$
Or $h'(x)=a\ $ et $\ h''(x)=0.$ Donc, l'équation devient :
$$2a+(ax+b)=x+3$$
c'est à dire
$$(a-1)x+2a+b=0\ \text{ ou }\ \left\lbrace\begin{array}{rcl} a-1&=&0\\2a+b&=&0\end{array}\right.$$
Donc, $a=1\ $ et $\ b=-2.$ Finalement
$$\boxed{h(x)=x-2}$$
3) Soit $g$ une solution de $(E')$ c'est à dire une fonction telle que :
$$g''(x)+2g'(x)+g(x)=x+3\quad (2)$$
En faisant la différence membre à membre de (2) et (1) on trouve :
$$g''(x)-h''(x)+2g'(x)-2h'(x)+g(x)-h(x)=0$$
c'est à dire
$$(g-h)''(x)+2(g-h)'(x)+(g-h)(x)=0\quad (3)$$
Ce qui montre que la fonction $g-h$ est solution de $(E).$
Réciproquement $g-h$ est solution de $(E)$ est équivalent à (3) soit à :
$$g''(x)+2g'(x)+g(x)=h''(x)+2h'(x)+h(x)\quad (4)$$
Or, d'après (1) le second membre de cette relation vaut $x+3.$ Donc, (4) est équivalent à
$$g''(x)+2g'(x)+g(x)=x+3$$
Autrement dit $g$ est solution de $(E').$
4) La fonction $k$ est continue sur son ensemble de définition $D_{k}$ qui est égal à $\mathbb{R}$ ; de plus
$$\lim_{x\rightarrow -\infty}k(x)=-\infty\;;\quad\lim_{x\rightarrow +\infty}k(x)=0$$
et
$$\forall\;x\in D_{k}\;,\quad k'(x)=-(x+1)\mathrm{e}^{-x}$$
$k'$ s'annule au point $-1$ et est $>0$ si, et seulement si, $x+1<0$ c'est à dire $x<-1.$
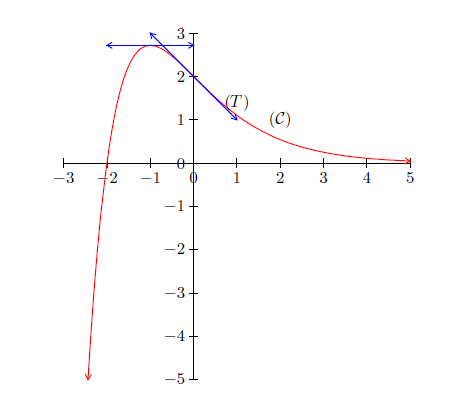
Pour que le point $I(0\;,\ 2)$ soit un point d'inflexion de la courbe $(\mathcal{C})$ il suffit que $k$ soit deux fois dérivable et qu'au point $O\;,\ k''$ "s'annule en changeant de signe".
Cela est bien le cas puisque $k''(x)=x\mathrm{e}^{-x}$ s'annule au point $O$, et est $>0$ "après $O"$ et négatif "avant $O".$
Voici le tableau de variations de $k.$
$\text{T.V de }\ x\longmapsto k(x)=(x+2)\mathrm{e}^{-x}$
$$\begin{array}{|c|lcccr|}\hline x&-\infty&&-1&&+\infty\\ \hline k'(x)&&+&0&-&\\ \hline&&&\mathrm{e}&&\\k&&\nearrow&\vdots&\searrow&\\&-\infty&&&&0\\ \hline\end{array}$$
et voici la courbe représentative de $k.$
Exercice 4
1) a) La fonction $f$ est continue et dérivable sur $D_{f}=]-1\;,\ +\infty[$ et
$$\lim_{x\rightarrow -1}f(x)=-\infty\;;\quad\lim_{x\rightarrow +\infty}f(x)=+\infty$$
et
$$\forall\;x\in D_{f}\;,\ f'(x)=2\dfrac{1}{1+x}$$
La dérivée est donc strictement positive dans $D_{f}.$
Voici le tableau de variation de $f.$
$\text{T.V de }\ x\longmapsto f(x)=2\ln(1+x)$
$$\begin{array}{|c|lcr|}\hline x&-1&&+\infty\\ \hline f'(x)&&+&\\ \hline&&&+\infty\\f&&\nearrow&\\&-\infty&&\\ \hline\end{array}$$
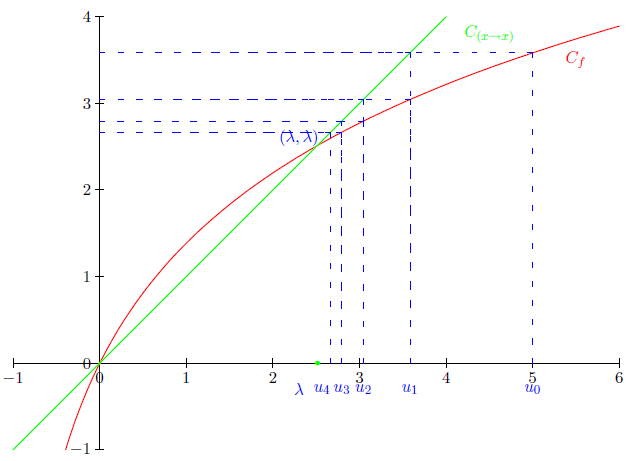
et voici la courbe $\mathcal{C}_{f}$ ainsi que les quatre premiers termes de la suite sur le graphique.
b) La fonction $\ell$ est continue et dérivable sur $D_{f}$ et
$$\lim_{x\rightarrow -1}f(x)=-\infty\;;\quad\forall\;x\in D_{f}\;,\ \ell'(x)=f'(x)-1=\dfrac{1-x}{1+x}$$
Lorsque $x$ tend vers $+\infty$, nous sommes en présence d'une indétermination de la forme $"+\infty-\infty"$, mais on peut écrire :
$$\ell(x)=2x\left(\dfrac{\ln(1+x)}{x}-\dfrac{1}{2}\right)$$
Lorsque $x$ tend vers $+\infty\;,\ \dfrac{\ln(1+x)}{x}$ a pour limite $0.$
Donc, le facteur $\dfrac{\ln(1+x)}{x}-\dfrac{1}{2}$ a pour limite $-\dfrac{1}{2}.$ Par conséquent
$$\lim_{x\rightarrow +\infty}\ell(x)=-\infty$$
Voici le tableau de variation de $\ell.$
$\text{T.V de }\ x\longmapsto \ell(x)=f(x)-x\;;\ \alpha=\ell(2)=2\ln 3-2\sim 2.2$
$$\begin{array}{|c|lcccr|}\hline x&2&&\lambda&&+\infty\\ \hline\ell'(x)&&-&&-&\\ \hline&\alpha&&\vdots&&\\&&\searrow&\vdots&&\\&&&0&&\\ \ell&&&\vdots&\searrow&\\&&&\vdots&&-\infty\\ \hline\end{array}$$
La fonction $\ell$ étant continue et strictement décroissante dans $I=[2\;,\ +\infty[$, réalise une bijection de $I$ dans $\ell(I)=J=]-\infty_;,\ \alpha[$; et puisque le réel $0$ appartient à $J$, il a dans l'intervalle $I$ un seul antécédent par $\ell.$
Autrement dit, l'équation $\ell(x)=0$ a dans $I$ une solution unique $\lambda.$
Ce $\lambda$ est alors l'unique élément de $I$ tel que $f(\lambda)=\lambda.$
2) a) Voir graphique.
b) La fonction $f$ étant continue et strictement croissante dans $I=[2\;,\ +\infty[$, réalise une bijection de $I$ dans $f(I)=[f(2)\;,\ +\infty[$ ; et puisque $f(2)=2\ln 3\sim 2.19$ est $>2\;,\ f(I)$ est contenu dans $I.$
Démontrons maintenant par récurrence la propriété :
$$\forall\;n\in\mathbb{N}\;,\ P_{n}\ \text{ est vraie, avec }\ P_{n}\ :\ "U_{n}\geq 2"$$
Initialisation : $U_{0}=5$, donnée de l'énoncé. Donc, $U_{0}\geq 2\ $ et $\ P_{0}$ est vraie.
Héritage : Supposons la propriété vérifiée jusqu'à un rang $n$, en particulier $P_{n}$ vraie (c'est à dire $U_{n}\geq 2\ $ ou $\ U_{n}\in I)$ et montrons que $P_{n+1}$ est vraie.
$$\begin{array}{rcl}\left.\begin{array}{rcl} U_{n}&\in&I\quad\text{(Hypothèse de récurrence)}\\f(I)&\subset&I\\U_{n+1}&=&f(U_{n})\end{array}\right\rbrace&\Rightarrow&U_{n+1}=f(U_{n})\in I\\&\Leftrightarrow&U_{n+1}\geq 2\end{array}$$
c) $\forall\;x\in]2\;,\ +\infty[\;,\ f'(x)=\dfrac{2}{1+x}$ ; donc,
$$\forall\;x\in]2\;,\ +\infty[\;,\ 0\leq f'(x)\leq\dfrac{2}{1+2}=\dfrac{2}{3}$$
Conclusion :
$$\forall\;x\in]2\;,\ +\infty[\;,\quad |f'(x)|\leq\dfrac{2}{3}$$
d) Soit $n\in\mathbb{N}.$ Les réels $U_{n}\ $ et $\ \lambda$ appartiennent à $[2\;,\ +\infty[$, intervalle dans lequel $|f'|\leq\dfrac{2}{3}$, on peut donc appliquer l'inégalité des accroissements finis au couple $(U_{n}\;,\ \lambda)\ :$
$$|f(U_{n})-f(\lambda)|\leq\dfrac{2}{3}|U_{n}-\lambda|$$
c'est à dire , puisque $f(\lambda)=\lambda$
$$|U_{n+1}-\lambda|\leq\dfrac{2}{3}|U_{n}-\lambda|$$
Posons $|U_{n}-\lambda|=\delta_{n}$ ; la relation précédente devient alors
$$0<\delta_{n+1}\leq\dfrac{2}{3}\delta_{n}\quad(1)$$
Si au lieu de $"\leq"$ on avait $"="$, la suite $\delta_{n}$ serait une suite géométrique et on pourrait immédiatement écrire
$$\delta_{n+1}=\left(\dfrac{2}{3}\right)^{n}\delta_{0}$$
C'est pourquoi d'aucuns disent d'une suite vérifiant (1) qu'elle est sous-géométrique.
Utilisons la même méthode : donnons à $n$ toutes les valeurs entières possibles entre $0\ $ et $\ p\;,\ p$ entier $\geq 0$ ; multiplions ensuite membre à membre (Nous sommes en droit de le faire par ce que nous manipulons des nombres positifs).
Il vient :
$$\delta_{0}\delta_{1}\ldots\delta_{p}\delta_{p+1}\leq\dfrac{2}{3}\delta_{0}\dfrac{2}{3}\delta_{1}\ldots\dfrac{2}{3}\delta_{p}$$
et en simplifiant par $\delta_{0}\delta_{1}\ldots\delta_{p}\ :\ 0<\delta_{p+1}\leq\left(\dfrac{2}{3}\right)^{p+1}\delta_{0}$ ; c'est à dire (tout en remplaçant $p$ par $n)$
$$\forall\;n\in\mathbb{N}\;,\quad 0<|U_{n+1}-\lambda|\leq\left(\dfrac{2}{3}\right)^{n+1}|U_{0}-\lambda|\quad(2)$$
$\ell(2)\sim 2.2$ est positif, $\ell(3)\sim -2.2$ est négatif, donc d'après le théorème des valeurs intermédiaires, $\lambda$ est compris entre $2\ $ et $\ 3.$
Puisque $U_{0}=5$, on en déduit que $|U_{0}-\lambda|\leq 3$ et la relation (2) entraîne :
$$\forall\;n\in\mathbb{N}\;,\quad 0<|U_{n+1}-\lambda|\leq 3\left(\dfrac{2}{3}\right)^{n+1}=2\left(\dfrac{2}{3}\right)^{n}$$
Cette dernière relation s'écrit aussi :
$$\forall\;n\in\mathbb{N}\;,\quad 0<\delta_{n+1}\leq 2\left(\dfrac{2}{3}\right)^{n}$$
En remarquant que $\lim_{n\rightarrow +\infty}2\left(\dfrac{2}{3}\right)^{n}=0$, on conclut par le théorème des gendarmes que
$$\lim_{n\rightarrow +\infty}\delta_{n+1}=0\;,\ \text{soit : }\lim_{n\rightarrow +\infty}\delta_{n}=0$$
C'est à dire
$$\lim_{n\rightarrow +\infty}|U_{n}-\lambda|=0$$
Enfin :
$$\lim_{n\rightarrow +\infty}U_{n}=\lambda$$
e) La relation $\forall\;n\in\mathbb{N}\;,\ |U_{n+1}-\lambda|\leq 2\left(\dfrac{2}{3}\right)^{n}$ s'écrit aussi :
$$\forall\;n\in\mathbb{N}^{*}\;,\quad|U_{n}-\lambda|\leq 2\left(\dfrac{2}{3}\right)^{n-1}$$
Donc, pour qu'un entier $n$ vérifie $|U_{n}-\lambda|\leq\dfrac{1}{10^{2}}$, il suffit que $2\left(\dfrac{2}{3}\right)^{n-1}\leq\dfrac{1}{10^{2}}$
Cette relation est équivalente à :
$$\ln\left(\dfrac{2}{3}\right)^{n-1}\leq\ln\dfrac{1}{200}$$
c'est à dire
$$(n-1)\ln\dfrac{2}{3}\leq -\ln 200\quad\text{ou}\quad n-1\geq\dfrac{\ln 200}{\ln 3-\ln 2}$$
Finalement
$$n\geq\dfrac{\ln 200}{\ln 3-\ln 2}+1$$
Le plus petit entier vérifiant cette relation est :
$$\boxed{p=E\left(\dfrac{\ln 200}{\ln 3-\ln 2}+1\right)+1=15}$$

Ajouter un commentaire