Corrections Série d'exercices : Statistique - 2nd L

Exercice 1:

Partie A:

Tableau initial:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline\text{Notes }&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16&17\\
\hline \text{Effectifs }&2&1&1&2&3&2&4&6&7&6&5&3&2&3&2&1\\\hline\end{array}$

1. Compléter le tableau avec ECC, ECD, Fréquence en %, et FCC en %:

•  Effectif Cumulé Croissant (ECC): Cumul des effectifs au fur et à mesure.
•  Effectif Cumulé Décroissant (ECD): Cumul des effectifs à partir de la fin.
• Fréquence en %: (Effectif / Total) * 100
• FCC en %: (ECC / Total) * 100

Calculs:

Total des effectifs (N) = 2+1+1+2+3+2+4+6+7+6+5+3+2+3+2+1 = 50

Tableau complété:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline\text{Notes }&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16&17\\
\hline \text{Effectifs }&2&1&1&2&3&2&4&6&7&6&5&3&2&3&2&1\\
\hline \text{ECC }&2&3&4&6&9&11&15&21&28&34&39&42&44&47&49&50\\
\hline \text{ECD }&50&49&47&46&44&41&39&35&29&22&16&11&8&6&3&1\\
\hline \text{Fréquence }&4&2&2&4&6&4&8&12&14&12&10&6&4&6&4&2\\
\hline \text{FCC en % }&4&6&8&12&18&22&30&42&56&68&78&84&88&94&98&100\\
\hline\end{array}$

2. Nombre d'élèves qui ont au moins $9$:

Cela correspond à l'effectif des notes ≥ 9. On peut le calculer à partir de l'ECD de 9 ou en additionnant les effectifs à partir de 9:

$7 (10) + 6 (11) + 5 (12) + 3 (13) + 2 (14) + 3 (15) + 2 (16) + 1 (17) = 29$

3. Que représente ECC de la modalité 8?

ECC de 8 est 15, cela signifie que 15 élèves ont une note inférieure ou égale à 8.

4. Pourcentage des élèves qui ont moins de 14:

C'est le FCC de 13 (car moins de 14 correspond à ≤13):

FCC de 13 = 84%

5. Calculs des indicateurs statistiques:

• Mode: Note avec le plus grand effectif → 10 (effectif 7)
• Médiane: N = 50 → médiane est la moyenne des 25ème et 26ème valeurs.  ECC: 21 (≤9), 28 (≤10) → 25ème et 26ème sont 10 → Médiane = 10
• Étendue: 17 - 2 = 15
• Moyenne (M):

 \[
  \begin{array}{rcl}
 M &=&\dfrac{\sum (note \times effectif)}{N}\\\\&=&\dfrac{2\times 2 + 3\times 1 + 4\times 1 + 5\times 2 + 6\times 3 + 7\times 2 + 8\times 4 + 9\times 6 + 10\times 7 + 11\times 6 + 12\times 5 + 13\times 3 + 14\times 2 + 15\times 3 + 16\times 2 + 17\times 1}{50}
                                     \\\\&=& \dfrac{4 + 3 + 4 + 10 + 18 + 14 + 32 + 54 + 70 + 66 + 60 + 39 + 28 + 45 + 32 + 17}{50}
                                      \\\\ &=&\dfrac{496}{50}
                                       \\ \\&=&9.92
\end{array}
 \]
 

• Variance (V):

  \[
  V = \dfrac{\sum (note^2 \times effectif)}{N} - M^2
  \]
  Calcul des carrés:

 
\[
\begin{array}{rcl}
\sum (note^2 \times effectif) &=&4\times 2 + 9\times 1 + 16\times 1 + 25\times 2 + 36\times 3 + 49\times 2 + 64\times 4 + 81\times 6 + 100\times 7 + 121\times 6 + 144\times 5 + 169\times 3 + 196\times 2 + 225\times 3 + 256\times 2 + 289\times 1
                                     \\\\&=& 8 + 9 + 16 + 50 + 108 + 98 + 256 + 486 + 700 + 726 + 720 + 507 + 392 + 675 + 512 + 289
                                      \\\\ &=&5252
\end{array}
 \]
 

\[
\begin{array}{rcl}
V &=& \dfrac{5252}{50} - 9.92^2
       \\\\&=& 105.04 - 98.4064
         \\\\ &=&6.6336
\end{array}
 \]

• Écart-type (σ):

\[
\begin{array}{rcl}
σ &=& \sqrt{V}
       \\\\&=& \sqrt{6.6336}
         \\\\ &≈&2.5756$
\end{array}
 \]

Partie B:

1. Regroupement en classes d'amplitude 4:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline\text{Notes }&[0;4[&[4;8[&[8;12[&[12;16[&[16;20[&\text{Totaux}\\
\hline \text{Effectifs }&2+1+1=4&2+3+2+4=11&6+7+6+5=24&3+2+3=8&2+1=3&50\\
\hline \text{ECC }&4&15&39& 47&50&-\\
\hline\end{array}$

2. Nombre d'élèves qui ont moins de 12:

Cela correspond à la somme des effectifs des classes [0;4[, [4;8[, [8;12[ mais seulement partie de [8;12[. Cependant, avec les classes regroupées, on prend toute la classe [8;12[ car 12 est exclu. Donc ECC avant [12;16[ est 39.

3. Pourcentage d'élèves qui ont au moins 8:

Cela correspond à l'effectif des classes [8;12[, [12;16[, [16;20[ = 24 + 8 + 3 = 35 → 35/50 * 100 = 70%

4. Classe médiane et moyenne:

- Classe médiane: N/2 = 25 → classe [8;12[ (ECC passe de 15 à 39)
- Moyenne: On utilise les centres de classes (2, 6, 10, 14, 18):
  \[
  M = \dfrac{4*2 + 11*6 + 24*10 + 8*14 + 3*18}{50} = \dfrac{8 + 66 + 240 + 112 + 54}{50} = \dfrac{480}{50} = 9.6
  \]

Exercice 2:

Notes: $12$, $4$, $16$, $16$, $16$, $7$, $9$, $12$, $9$, $12$

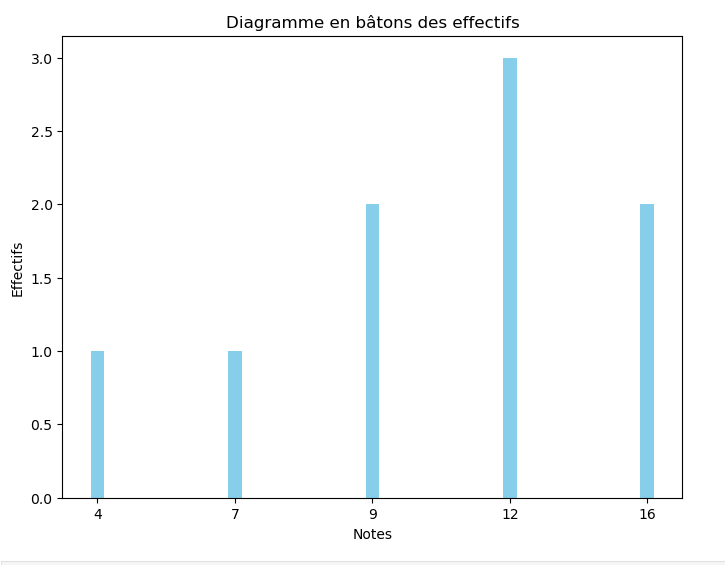
1. Tableau d'effectifs et diagramme en bâtons:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline\text{Notes }&4&7&9&12&16\\
\hline \text{Effectifs }&1&1&2&3&3\\
\hline\end{array}$

Diagramme en bâtons:

2. Calculs:

- Étendue: $16 - 4 = 12$
- Moyenne:
  \[
  M = \dfrac{4 + 7 + 9*2 + 12*3 + 16*3}{10} = \dfrac{4 + 7 + 18 + 36 + 48}{10} = \dfrac{113}{10} = 11.3
  \]
- Médiane: 10 notes → moyenne des 5ème et 6ème.
  Ordonnées: 4, 7, 9, 9, 12, 12, 12, 16, 16, 16 → 12 et 12 → Médiane = 12
- Quartiles:
  - Q1: 1/4 * 10 = 2.5 → 3ème valeur → 9
  - Q3: 3/4 * 10 = 7.5 → 8ème valeur → 16

3. Écart-type et variance:

- Variance:
  \[
  V = \dfrac{4^2 + 7^2 + 2*9^2 + 3*12^2 + 3*16^2}{10} - 11.3^2 = \dfrac{16 + 49 + 162 + 432 + 768}{10} - 127.69 = \dfrac{1427}{10} - 127.69 = 142.7 - 127.69 = 15.01
  \]
- Écart-type: √15.01 ≈ 3.874

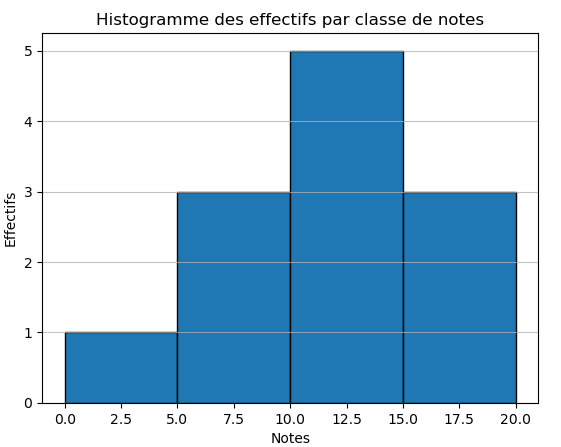
4. Regroupement en classes:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline\text{Notes }&[0;5[&[5;10[& [10;15[&[15;20\\
\hline \text{Effectifs }&1&3&5&3\\
\hline\end{array}$

Histogramme:

Exercice 3:

Tableau initial:

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline\text{Tailles (cm)  }&[145;155[&[155;165[&[165;175[&[175;185[&[185;200[ \\
\hline \text{Effectifs }&25&73&84&64&4\\
\hline\end{array}$

1. Centres de classes:

Centres = (borne inf + borne sup)/2 → 150, 160, 170, 180, 192.5

2. Moyenne, variance, écart-type:

 Moyenne:
  \[
  M = \dfrac{25*150 + 73*160 + 84*170 + 64*180 + 4*192.5}{25 + 73 + 84 + 64 + 4} = \dfrac{3750 + 11680 + 14280 + 11520 + 770}{250} = \dfrac{42000}{250} = 168
  \]
Variance:
  \[
  V = \dfrac{25*150^2 + 73*160^2 + 84*170^2 + 64*180^2 + 4*192.5^2}{250} - 168^2
  \]
  Calcul des carrés:
  \[
  25*22500 + 73*25600 + 84*28900 + 64*32400 + 4*37056.25 = 562500 + 1868800 + 2427600 + 2073600 + 148225 = 7074725
  \]
  \[
  V = \dfrac{7074725}{250} - 28224 = 28298.9 - 28224 = 74.9
  \]
Écart-type: √74.9 ≈ 8.655

3. Histogramme des fréquences cumulées en %:

     Fréquence cumulée pour chaque classe:
      $ [145;155[: 25/250 = 10%.$
      $ [155;165[: (25+73)/250 = 39.2%$.
      $ [165;175[: (25+73+84)/250 = 72.8%$.
      $ [175;185[: (25+73+84+64)/250 = 97.6%$.
      $ [185;200[: 100%$.

4. Calcul de N/2 et 3N/4:

$N = 250$.
$N/2 = 125$ → classe médiane $[165;175[$.
$3N/4 = 187.5$ → classe $[175;185[$.