Correction Serie d'exercices : Fonction exponentielle- TL
Exercice 1
\[ A = \frac{e^{5x} \times e^{-2x}}{e^{-x+2}} = \frac{e^{5x-2x}}{e^{-x+2}} = e^{5x-2x+x-2} = e^{4x-2} \]
Exercice 2
1. \( (E) \) équivaut à \( x(e^x-1) = 0 \), donc \( x = 0 \) ou \( e^x = 1 \).
Solution : \( S_{\mathbb{R}} = \{ 0 \} \).
2. Tableau de signes pour \( (I) \):
\[
\begin{array}{|c|c|c|c|c|c|c|}
\hline
x & -\infty & -2 & 0 & 1 & +\infty \\
\hline
x^2 + x - 2 & + & - & - & + & + \\
\hline
e^{2x} - 1 & - & - & 0 & + & + \\
\hline
f(x) & - & + & \big| & - & + \\
\hline
\end{array}
\]
Solution : \( S_{\mathbb{R}} = [-2; 0[ \cup [1; +\infty[ \).
Exercice 3 : Dérivation
a) $f(x) = e^{-2x+1}$
$$
f'(x) = e^{-2x+1} \cdot (-2)
$$
$f'(x) = -2e^{-2x+1}$
b) $f(x) = x + 2 - e^x$
$$
f'(x) = 1 - e^x
$$
$f'(x) = 1 - e^x$
c) $f(x) = (1 - x)e^x$
Produit : $u(x) = 1 - x, \quad v(x) = e^x$
$$
f'(x) = u'v + uv' = (-1)e^x + (1 - x)e^x = (1 - x - 1)e^x = -x e^x
$$
$f'(x) = -x e^x$
Exercice 4 : Limites
a) $f(x) = (2x+1)e^x + \frac{1}{x}$, $x \to +\infty$
$(2x+1)e^x \to +\infty$
$\frac{1}{x} \to 0$
Limite : $+\infty$
b) $f(x) = 2 \cdot \frac{e^x - 1}{x} + x^2$, $x \to 0$
Utiliser $\lim_{x \to 0} \frac{e^x - 1}{x} = 1$
$$
\lim_{x \to 0} f(x) = 2 \cdot 1 + 0 = 2
$$
Limite : $2$
Exercice 5 : Primitives
a) $f(x) = e^{4x} \Rightarrow \int e^{4x} dx = \frac{1}{4}e^{4x} + C$
Primitive: $ F(x) = \frac{1}{4} e^{4x} $
b) $\int e^{3x} dx = \frac{1}{3}e^{3x}, \quad \int e^{-\frac{1}{2}x} dx = -2e^{-\frac{1}{2}x}, \quad \int 5dx = 5x$
Primitive : $F(x) =\frac{1}{3}e^{3x} + 2e^{-\frac{1}{2}x} + 5x $
c) $\int (x - \frac{3}{4}) dx + \int 3e^{-2x+1} dx$
$\int x dx = \frac{x^2}{2}, \int -\frac{3}{4} dx = -\frac{3}{4}x$
$\int 3e^{-2x+1} dx = -\frac{3}{2}e^{-2x+1}$
Primitive : $F(x) =\frac{x^2}{2} - \frac{3}{4}x - \frac{3}{2}e^{-2x+1} $
Exercice 6 : QCM
1.
$
\dfrac{e^{2x} - e^x}{e^x + 1} = \dfrac{e^x(e^x - 1)}{e^x + 1} = \boxed{\text{Réponse B}}
$
2.
$
x^2 - x - 1 = 3x - 4 \Rightarrow x^2 - 4x + 3 = 0 \Rightarrow x = 1 \text{ ou } x = 3 \Rightarrow \boxed{\text{Réponse C}}
$
3.
$e^x - 2x \to +\infty$ car $e^x \gg 2x \Rightarrow \boxed{\text{Réponse A}}$
4.
$f(x) = xe^{-2x} \Rightarrow f'(x) = e^{-2x} + x(-2e^{-2x}) = (1 - 2x)e^{-2x} \Rightarrow \boxed{\text{Réponse C}}$
Exercice 7
a)
$(e^{2x})^{2} \times (e^{x})^{2} = e^{4x} \times e^{-2x} = e^{4x - 2x} = e^{2x}$
b)
$
(e^{x} + e^{-x})^{2} - (e^{x} - e^{-x})^{2} = (e^{x} + e^{-x} - e^{x} + e^{-x})(e^{x} + e^{-x} + e^{x} - e^{-x})= (2e^{-x})(2e^{x}) = 4e^{-x}e^{x} = 4
$
Exercice 8
- Signe de B
\[ B = e^{2x} + e^x - 2 \]
Posons \( e^x = X \), donc \( X > 0 \). On a \( X^2 + X - 2 \).
\[ \Delta = 1 + 8 = 9 \]
\[ X = -2 \quad \text{ou} \quad X = 1 \]
Étudions le signe de \( X^2 + X - 2 \).
\begin{array}{|c|ccccc|}
\hline
X & -\infty & -2 & 1 & +\infty \\
\hline
X^2 + X - 2 & + & 0 & - & 0 & + \\
\hline
\end{array}
\( X^2 + X - 2 \geq 0 \iff X \in ]-\infty; -2] \cup [1; +\infty[ \)
On a : \( e^x \in ]-\infty; -2] \) ou : \( e^x \in [1; +\infty[ \)
\( e^x \leq -2 \) est impossible ou \( e^x \geq 1 \) équivaut à \( x \geq \ln 1 \)
Pour \( x \in [0; +\infty[ \), \( e^{2x} + e^x - 2 > 0 \)
Pour \( x \in ]-\infty; 0] \), \( e^{2x} + e^x - 2 < 0 \)
- Signe de C}
\[ C = e^x - 2e^{-x} + 1 = \frac{e^{2x} + e^x - 2}{e^x} \]
Comme pour \( x \in \mathbb{R} \), \( e^x > 0 \) donc le signe de C est le même que celui de B.
Exercice 9 : Déterminer les limites en \( +\infty \) et \( -\infty \)
a) \( f(x) = \dfrac{e^{x+1}}{e^x + 2} \)
Limite en \( +\infty \) :
Quand \( x \to +\infty \), \( e^x \) domine, donc le dénominateur \( e^x + 2 \approx e^x \).
Ainsi :
\[ f(x) \approx \dfrac{e^{x+1}}{e^x} = e^{x+1 - x} = e^1 = e \]
Donc :
\[ \lim_{x \to +\infty} f(x) = e \]
Limite en \( -\infty \) :
Quand \( x \to -\infty \), \( e^x \to 0 \), donc :
\[ f(x) \approx \dfrac{e^{x+1}}{0 + 2} = \dfrac{e^{x+1}}{2} \to 0 \]
Donc :
\[ \lim_{x \to -\infty} f(x) = 0 \]
b) \( f(x) = \dfrac{x e^x}{x + 1} \)
Limite en \( +\infty \) :
Quand \( x \to +\infty \), \( e^x \) croît beaucoup plus vite que \( x \), donc le numérateur \( x e^x \) domine le dénominateur \( x + 1 \approx x \).
Ainsi :
\[ f(x) \approx \dfrac{x e^x}{x} = e^x \to +\infty \]
Donc :
\[ \lim_{x \to +\infty} f(x) = +\infty \]
Limite en \( -\infty \) :
Quand \( x \to -\infty \), \( e^x \to 0 \), et le dénominateur \( x + 1 \to -\infty \).
Le numérateur \( x e^x \) est le produit de \( x \to -\infty \) et \( e^x \to 0 \). On a une forme indéterminée \( -\infty \times 0 \).
Réécrivons \( f(x) \) :
\[ f(x) = \dfrac{x e^x}{x + 1} = \dfrac{x}{x + 1} \cdot e^x \]
Quand \( x \to -\infty \), \( \dfrac{x}{x + 1} \to 1 \) (car \( \dfrac{x}{x(1 + 1/x)} = \dfrac{1}{1 + 1/x} \to 1 \)).
Donc :
\[ f(x) \approx 1 \cdot e^x \to 0 \]
Donc :
\[ \lim_{x \to -\infty} f(x) = 0 \]
c)
Pour déterminer les limites de la fonction \( f(x) = \dfrac{e^{x} + 1}{e^x + 2} \) en \( +\infty \) et en \( -\infty \), nous allons analyser séparément chaque cas.
1. Limite en \( +\infty \) :
Quand \( x \to +\infty \), \( e^x \) tend vers \( +\infty \). On peut factoriser \( e^x \) au numérateur et au dénominateur :
\[
f(x) = \dfrac{e^{x} + 1}{e^x + 2} = \dfrac{e^x \left(1 + \dfrac{1}{e^x}\right)}{e^x \left(1 + \dfrac{2}{e^x}\right)} = \dfrac{1 + \dfrac{1}{e^x}}{1 + \dfrac{2}{e^x}}
\]
Quand \( x \to +\infty \), \( \dfrac{1}{e^x} \to 0 \) et \( \dfrac{2}{e^x} \to 0 \). Ainsi :
\[
\lim_{x \to +\infty} f(x) = \dfrac{1 + 0}{1 + 0} = 1
\]
Conclusion :
\[
\boxed{ \lim_{x \to +\infty} \dfrac{e^{x} + 1}{e^x + 2} = 1 }
\]
2. Limite en \( -\infty \) :
Quand \( x \to -\infty \), \( e^x \) tend vers \( 0 \). On a donc :
\[
f(x) = \dfrac{e^{x} + 1}{e^x + 2} \approx \dfrac{0 + 1}{0 + 2} = \dfrac{1}{2}
\]
Conclusion :
\[
\boxed{ \lim_{x \to -\infty} \dfrac{e^{x} + 1}{e^x + 2} = \dfrac{1}{2} }
\]
Exercice 10 : Trouver une primitive de \( f \) sur \( \mathbb{R} \)
a) \( f(x) = e^{3x} - e^{-\dfrac{1}{2}x} + 5 \)
On intègre terme à terme :
1. \( \int e^{3x} \, dx = \dfrac{1}{3} e^{3x} + C \)
2. \( \int -e^{-\dfrac{1}{2}x} \, dx = -\left( \dfrac{1}{-1/2} e^{-\dfrac{1}{2}x} \right) + C = 2 e^{-\dfrac{1}{2}x} + C \)
3. \( \int 5 \, dx = 5x + C \)
Une primitive \( F \) de \( f \) est donc :
\[ F(x) = \dfrac{1}{3} e^{3x} + 2 e^{-\dfrac{1}{2}x} + 5x + C \]
(où \( C \) est une constante réelle).
b) \( f(x) = \dfrac{e^{2x}}{1 + e^{2x}} \)
On reconnaît une forme \( \dfrac{u'}{u} \), où \( u = 1 + e^{2x} \) et \( u' = 2 e^{2x} \).
Ainsi :
\[ f(x) = \dfrac{e^{2x}}{1 + e^{2x}} = \dfrac{1}{2} \cdot \dfrac{2 e^{2x}}{1 + e^{2x}} = \dfrac{1}{2} \cdot \dfrac{u'}{u} \]
Donc une primitive est :
\[ F(x) = \dfrac{1}{2} \ln|u| + C = \dfrac{1}{2} \ln(1 + e^{2x}) + C \]
(On peut omettre la valeur absolue car \( 1 + e^{2x} > 0 \)).
c) \( f(x) = (2x - 3) e^{-x^2 + 3x + 1} \)
On reconnaît une forme \( u' e^u \), où \( u = -x^2 + 3x + 1 \) et \( u' = -2x + 3 \).
Ajustons le coefficient :
\[ 2x - 3 = -(-2x + 3) = -u' \]
Ainsi :
\[ f(x) = (2x - 3) e^{u} = -u' e^{u} \]
Une primitive de \( u' e^{u} \) est \( e^{u} \), donc une primitive de \( -u' e^{u} \) est \( -e^{u} \).
Donc :
\[ F(x) = -e^{-x^2 + 3x + 1} + C \]
Exercice 11
1. L'ensemble de définition de $f$ est $D_f = \mathbb{R}$.
2.
\[
\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} (1 - x + e^x) = +\infty,
\quad \text{car } \lim_{x \to -\infty} -x = +\infty, \quad \lim_{x \to -\infty} e^x = 0.
\]
3.
a) Pour tout nombre réel $x \neq 0$,
\[
f(x) = 1 - x + e^x = x \left( \frac{1}{x} - 1 + \frac{e^x}{x} \right).
\]
b)
\[
f(x) = 1 - x + e^x, \quad \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \left( x \left( \frac{1}{x} - 1 + \frac{e^x}{x} \right) \right).
\]
Comme $\lim_{x \to +\infty} \frac{1}{x} = 0$, $\lim_{x \to +\infty} \frac{e^x}{x} = +\infty$, on a
\[
\lim_{x \to +\infty} f(x) = +\infty.
\]
4. a)
\[
\lim_{x \to -\infty} \left( f(x) - (-x + 1) \right) = \lim_{x \to -\infty} e^x = 0.
\]
Donc la droite $(\Delta)$ d'équation $y = -x + 1$ est asymptote oblique à $(C)$ en $-\infty$.
b) On a :
\[
f(x) - (-x + 1) = e^x,
\]
donc le signe de $f(x) - (-x + 1)$ est celui de $e^x$; or pour tout réel $x$, $e^x > 0$, par suite $(C)$ est au-dessus de $(\Delta)$ sur $\mathbb{R}$.
5.
a) Pour tout élément $x$ de $\mathbb{R}$,
\[
f'(x) = -1 + e^x.
\]
b)
\[
f'(x) = 0 \iff -1 + e^x = 0 \iff e^x = 1 \iff x = 0.
\]
c)
\[
f'(x) > 0 \iff -1 + e^x > 0 \iff e^x > 1 \iff x > 0.
\]
d) Pour tout $x > 0$, $f'(x) > 0$, donc $f$ est strictement croissante sur $]0; +\infty[$.\\
Pour tout $x < 0$, $f'(x) < 0$, donc $f$ est strictement décroissante sur $]-\infty; 0[$.
\begin{array}{|c|c|c|c|}
\hline
x & -\infty & 0 & +\infty \\
\hline
f'(x) & - & 0 & + \\
\hline
f(x) & \searrow & 2 & \nearrow \\
\hline
\end{array}
6. Tableau de valeurs :
\[
\begin{array}{|c|c|c|c|c|c|c|}
\hline
x & -3 & -2 & -1 & 0 & 1 & 2 \\
\hline
f(x) & 4,05 & 3,39 & 2,39 & 2 & 2,78 & 6,59 \\
\hline
\end{array}
\]
7. Représentation graphique :
- Tracer \( C \) et \( \Delta \) sur \([-3; 2]\). 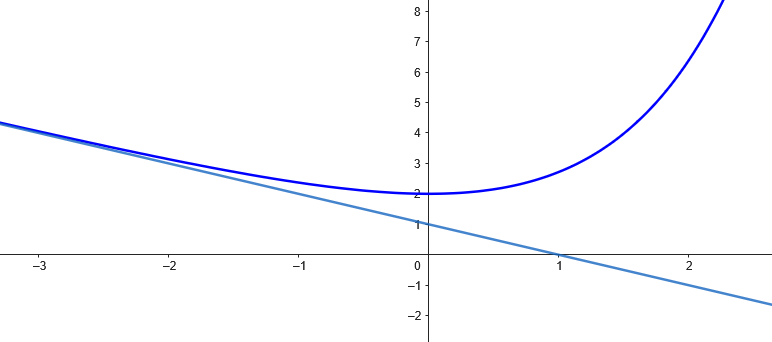
Exercice 12
Soit \( f(x) = (-2x + 3) e^x \) définie sur \( ]-\infty; 2] \).
1. Limite en \( -\infty \) :
\[
\lim_{x \to -\infty} f(x) = 0 \quad \text{car} \quad \lim_{x \to -\infty} (-2x + 3) e^x = 0.
\]
- Interprétation : La droite \( y = 0 \) est asymptote horizontale en \( -\infty \).
2. Dérivée et variations :
- \( f'(x) = (-2x + 1) e^x \).
- Signe de \( f'(x) \) :
- \( f'(x) > 0 \) pour \( x < \frac{1}{2} \).
- \( f'(x) < 0 \) pour \( x > \frac{1}{2} \).
- Tableau de variations :
\begin{array}{|c|c|c|c|}
\hline
x & -\infty & \frac{1}{2} & 2 \\
\hline
f'(x) & + & 0 & - \\
\hline
f(x) & \nearrow & 3,3 & \searrow\\
\hline
\end{array}
3. Points d'intersection :
- Avec l'axe des abscisses (\( A \)) :
\[
(-2x + 3) e^x = 0 \implies x = \frac{3}{2}, \quad A\left( \frac{3}{2}, 0 \right).
\]
- Avec l'axe des ordonnées (\( B \)) :
\[
f(0) = 3, \quad B(0, 3).
\]
4. Tableau de valeurs :
\[
\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
x & -4 & -3 & -2 & -1 & 0 & 0,5 & 1 & 1,5 & 2 \\
\hline
f(x) & 0,2 & 0,4 & 0,9 & 1,8 & 3 & 3,3 & 2,7 & 0 & -7,4 \\
\hline
\end{array}
\]
5. Représentation graphique :
- Tracer \( C \) sur \(]-\infty; 2]\). 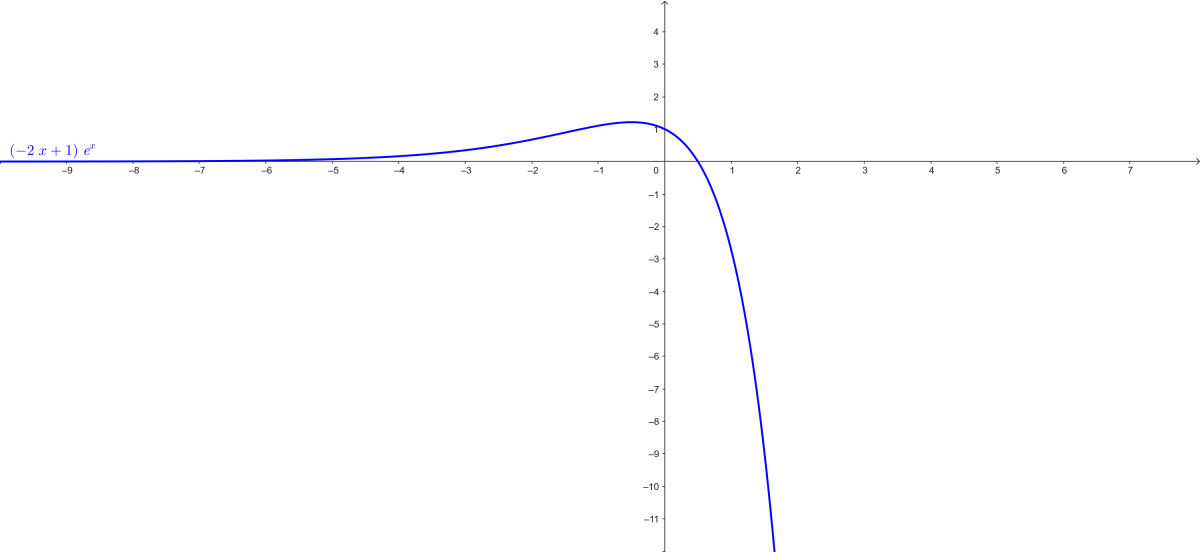
EXERCICE 13
1) Résoudre \( e^{2x+1} = e^{3x+7} \)
Les exponentielles sont égales si et seulement si leurs exposants sont égaux :
\[
2x + 1 = 3x + 7\Leftrightarrow -x = 6\Leftrightarrow x = -6
\]
\(\boxed{S=\{-6\}}\)
2) Résoudre \( e^{-x+17} = e^x \)
Égalité des exposants :
\[
-x + 17 = x\Leftrightarrow 17 = 2x\Leftrightarrow x = \frac{17}{2}
\]
\(\boxed{S=\{ \dfrac{17}{2}\}}\)
3) Résoudre \( e^{x+3} \times e^{x-2} = e^3 \)
On combine les exponentielles :
\[
e^{(x+3) + (x-2)} = e^3\Leftrightarrow e^{2x + 1} = e^3
\]
Égalité des exposants :
\[
2x + 1 = 3\Leftrightarrow 2x = 2\Leftrightarrow x = 1
\]
\(\boxed{ S=\{1\} }\)
4) Résoudre \( e^{2x} - 4e^x + 3 = 0 \)
Posons \( y = e^x \) :
\[
y^2 - 4y + 3 = 0\Leftrightarrow (y - 1)(y - 3) = 0\Leftrightarrow y = 1 \text{ ou } y = 3
\]
Donc :
\[
e^x = 1\Leftrightarrow x = 0 \quad \text{ou} \quad e^x = 3\Leftrightarrow x = \ln 3
\]
\(\boxed{S=\{ 0 ; \ln 3\} }\)
5) Résoudre \( e^{2(x+1)} - 8e^{x+2} - 9e^2 = 0 \)
Simplifions :
\[
e^{2x + 2} - 8e^{x + 2} - 9e^2 = 0\Leftrightarrow e^2(e^{2x} - 8e^x - 9) = 0
\]
Comme \( e^2 \neq 0 \), on a :
\[
e^{2x} - 8e^x - 9 = 0
\]
Posons \( y = e^x \) :
\[
y^2 - 8y - 9 = 0\Leftrightarrow (y - 9)(y + 1) = 0\Leftrightarrow y = 9 \text{ ou } y = -1
\]
Seule \( y = 9 \) est possible car \( e^x > 0 \) :
\[
e^x = 9\Leftrightarrow x = \ln 9 = 2 \ln 3
\]
\(\boxed{S=\{2 \ln 3\}}\)
6) Résoudre \( 2e^{2x-4} + 5e^{x-2} - 3 = 0 \)
Posons \( z = e^{x-2} \) :
\[
2z^2 + 5z - 3 = 0\Leftrightarrow z = \frac{-5 \pm \sqrt{25 + 24}}{4} = \frac{-5 \pm 7}{4}
\]
Donc \( z = \frac{1}{2} \) ou \( z = -3 \). Seule \( z = \frac{1}{2} \) est possible :
\[
e^{x-2} = \frac{1}{2}\Leftrightarrow x - 2 = -\ln 2\Leftrightarrow x = 2 - \ln 2
\]
\(\boxed{S=\{2 - \ln 2\}}\)
EXERCICE 14
1) Résoudre \( e^{3x+2} \leq e \)
L'exponentielle est croissante, donc :
\[
3x + 2 \leq 1\Leftrightarrow 3x \leq -1\Leftrightarrow x \leq -\frac{1}{3}
\]
\(\boxed{S=\left]-\infty, -\dfrac{1}{3}\right]}\)
2) Résoudre \( e^x - 7 < 0 \)
\[
e^x < 7\Leftrightarrow x < \ln 7
\]
\(\boxed{S=\left]-\infty, \ln 7\right[}\)
3) Résoudre \( e^{2x} - 9 > 0 \)
\[
e^{2x} > 9\Leftrightarrow 2x > \ln 9\Leftrightarrow x > \ln 3
\]
\(\boxed{S=\left]\ln 3, +\infty\right[}\)
4) Résoudre \( e^x + 1 > 0 \)
Toujours vrai car \( e^x > 0 \).
\(\boxed{S=\mathbb{R}}\)
5) Résoudre \( e^x(e^x - 4) < 0 \)
Posons \( y = e^x \) :
\[
y(y - 4) < 0\Leftrightarrow 0 < y < 4
\]
Donc :
\[
0 < e^x < 4\Leftrightarrow x < \ln 4
\]
\(\boxed{S=\left]-\infty, \ln 4\right[}\)
6) Résoudre \( e^{2x} + e^x - 6 \leq 0 \)
Posons \( y = e^x \) :
\[
y^2 + y - 6 \leq 0\Leftrightarrow (y + 3)(y - 2) \leq 0
\]
Le trinôme est négatif entre ses racines \( y = -3 \) et \( y = 2 \). Seul \( y \in [0, 2] \) est possible :
\[
0 \leq e^x \leq 2\Leftrightarrow x \leq \ln 2
\]
\(\boxed{S=\left]-\infty, \ln 2\right]}\)
7) Résoudre \( e^{2x} + e^x - 2 \geq 0 \)
Posons \( y = e^x \) :
\[
y^2 + y - 2 \geq 0\Leftrightarrow (y + 2)(y - 1) \geq 0
\]
Le trinôme est positif pour \( y \leq -2 \) ou \( y \geq 1 \). Seul \( y \geq 1 \) est possible :
\[
e^x \geq 1\Leftrightarrow x \geq 0
\]
\(\boxed{S=\left[0, +\infty\right[}\)
EXERCICE 15
1) Résoudre \( e^{2x} + e^x + 1 = 0 \)
Posons \( y = e^x \) :
\[
y^2 + y + 1 = 0\Leftrightarrow \Delta = -3 < 0\Leftrightarrow \text{Aucune solution réelle.}
\]
\(\boxed{S=\varnothing}\)
2) Résoudre \( e^x - 13e^x - 48 = 0 \)
Cette équation semble incorrecte (peut-être \( e^{2x} - 13e^x - 48 = 0 \)). Supposons :
\[
e^{2x} - 13e^x - 48 = 0
\]
Posons \( y = e^x \) :
\[
y^2 - 13y - 48 = 0\Leftrightarrow y = \frac{13 \pm \sqrt{169 + 192}}{2} = \frac{13 \pm 19}{2}
\]
Donc \( y = 16 \) ou \( y = -3 \). Seule \( y = 16 \) est possible :
\[
e^x = 16\Leftrightarrow x = \ln 16 = 4 \ln 2
\]
\(\boxed{S=\{4 \ln 2\}}\)
3) Résoudre \( 2e^{2x} + 5e^x + 8 = 0 \)
Posons \( y = e^x \) :
\[
2y^2 + 5y + 8 = 0\Leftrightarrow \Delta = -39 < 0\Leftrightarrow \text{Aucune solution réelle.}
\]
\(\boxed{S=\varnothing}\)
4) Résoudre \( 2e^{2x} + 4e^x + 2 = 0 \)
Posons \( y = e^x \) :
\[
2y^2 + 4y + 2 = 0\Leftrightarrow y^2 + 2y + 1 = 0\Leftrightarrow (y + 1)^2 = 0\Leftrightarrow y = -1
\]
Aucune solution car \( e^x > 0 \).
\(\boxed{S=\varnothing}\)
5) Résoudre \( e^x - e^x - 6 = 0 \)
Cette équation semble incorrecte (peut-être \( e^{2x} - e^x - 6 = 0 \)). Supposons :
\[
e^{2x} - e^x - 6 = 0
\]
Posons \( y = e^x \) :
\[
y^2 - y - 6 = 0\Leftrightarrow y = 3 \text{ ou } y = -2
\]
Seule \( y = 3 \) est possible :
\[
e^x = 3\Leftrightarrow x = \ln 3
\]
\(\boxed{S=\{\ln 3\}}\)
EXERCICE 16
1) Calculer \( P(1) \) et factoriser \( P(x) \)
\[
P(1) = 1 - 1 - 4 + 4 = 0\Leftrightarrow (x - 1) \text{ est un facteur.}
\]
Division polynomiale ou identification :
\[
P(x) = (x - 1)(x^2 - 4) = (x - 1)(x - 2)(x + 2)
\]
2) Résoudre \( P(x) = 0 \)
\[
(x - 1)(x - 2)(x + 2) = 0\Leftrightarrow x = 1, 2, -2
\]
3) Résolution des équations liées
a) \( (\ln x)^3 - (\ln x)^2 - 4 \ln x + 4 = 0 \)
Posons \( y = \ln x \) :
\[
y^3 - y^2 - 4y + 4 = 0\Leftrightarrow (y - 1)(y - 2)(y + 2) = 0\Leftrightarrow y = 1, 2, -2
\]
Donc :
\[
\ln x = 1\Leftrightarrow x = e \\
\ln x = 2\Leftrightarrow x = e^2 \\
\ln x = -2\Leftrightarrow x = e^{-2}
\]
\(\boxed{S=\{e^{-2}; e; e^2\}}\)
b) \( e^{3x} - e^{2x} - 4e^x + 4 = 0 \)
Posons \( y = e^x \) :
\[
y^3 - y^2 - 4y + 4 = 0\Leftrightarrow (y - 1)(y - 2)(y + 2) = 0\Leftrightarrow y = 1, 2, -2
\]
Seules \( y = 1 \) et \( y = 2 \) sont possibles :
\[
e^x = 1\Leftrightarrow x = 0 \\
e^x = 2\Leftrightarrow x = \ln 2
\]
\(\boxed{S=\{0 ;\ln 2\}}\)
c) \( e^{3x} - e^{2x} - 4e^x + 4 \geq 0 \)
Posons \( y = e^x \) :
\[
(y - 1)(y - 2)(y + 2) \geq 0
\]
Étude du signe :
- Pour \( y \in ]-2, 1[ \) : négatif
- Pour \( y \in ]1, 2[ \) : positif
- Pour \( y > 2 \) : positif
Seuls \( y \in [1, 2] \) et \( y \geq 2 \) sont possibles :
\[
1 \leq e^x \leq 2\Leftrightarrow 0 \leq x \leq \ln 2 \\
e^x \geq 2\Leftrightarrow x \geq \ln 2
\]
\(\boxed{S=[0, +\infty[}\)
EXERCICE 17
1) Calculer \( h(-2) \) et résoudre \( h(x) = 0 \)
\[
h(-2) = 2(-8) - 4 - 8(-2) + 4 = -16 - 4 + 16 + 4 = 0\Leftrightarrow (x + 2) \text{ est un facteur.}
\]
Factorisation :
\[
h(x) = (x + 2)(2x^2 - 5x + 2)
\]
Résolution de \( 2x^2 - 5x + 2 = 0 \) :
\[
x = \frac{5 \pm \sqrt{25 - 16}}{4} = \frac{5 \pm 3}{4}\Leftrightarrow x = 2 \text{ ou } x = \frac{1}{2}
\]
Donc :
\[
h(x) = (x + 2)(x - 2)(2x - 1)
\]
Solutions $S$ de \( h(x) = 0 \) : \( \boxed{\{-2;\dfrac{1}{2};2\}}\)
Résolution de \( h(x) > 0 \) :
Étude du signe :
- Pour \( x < -2 \) : négatif
- Pour \( -2 < x < \frac{1}{2} \) : positif
- Pour \( \frac{1}{2} < x < 2 \) : négatif
- Pour \( x > 2 \) : positif
\(\boxed{S=\left]-2, \dfrac{1}{2}\right[ \cup \left]2, +\infty\right[}\)
2) Résolution des équations et inéquations liées
a) Équations :
\[
2e^{3x} - e^{2x} - 8e^x + 4 = 0
\]
Posons \( y = e^x \) :
\[
2y^3 - y^2 - 8y + 4 = 0\Leftrightarrow (y + 2)(y - 2)(2y - 1) = 0\Leftrightarrow y = -2, 2, \frac{1}{2}
\]
Seules \( y = 2 \) et \( y = \frac{1}{2} \) sont possibles :
\[
e^x = 2\Leftrightarrow x = \ln 2 \\
e^x = \frac{1}{2}\Leftrightarrow x = -\ln 2
\]
\(\boxed{ S=\{-\ln 2 ; \ln 2\}}\)
b) Inéquations :
\[
2e^{3x} - e^{2x} - 8e^x + 4 > 0
\]
Posons \( y = e^x \) :
\[
(y + 2)(y - 2)(2y - 1) > 0
\]
Étude du signe :
- Pour \( y \in ]0, \frac{1}{2}[ \) : positif
- Pour \( y \in ]\frac{1}{2}, 2[ \) : négatif
- Pour \( y > 2 \) : positif
Donc :
\[
0 < e^x < \frac{1}{2}\Leftrightarrow x < -\ln 2 \\
e^x > 2\Leftrightarrow x > \ln 2
\]
\(\boxed{S=\left]-\infty, -\ln 2\right[ \cup \left]\ln 2, +\infty\right[}\)
EXERCICE 18
1) Système :
\[
\begin{cases}
3e^x - 4e^y = -6 \\
2e^x + e^y = 7
\end{cases}
\]
Posons \( a = e^x \) et \( b = e^y \) :
\[
\begin{cases}
3a - 4b = -6 \\
2a + b = 7
\end{cases}
\]
De la deuxième équation : \( b = 7 - 2a \). Substituons dans la première :
\[
3a - 4(7 - 2a) = -6\Leftrightarrow 3a - 28 + 8a = -6\Leftrightarrow 11a = 22\Leftrightarrow a = 2
\]
Donc :
\[
b = 7 - 4 = 3
\]
Ainsi :
\[
e^x = 2\Leftrightarrow x = \ln 2 \\
e^y = 3\Leftrightarrow y = \ln 3
\]
\(\boxed{S=\{(\ln 2, \ln 3)\}}\)
2) Système :
\[
\begin{cases}
xy = -15 \\
e^x e^y = e^{-2}
\end{cases}
\]
La deuxième équation donne :
\[
e^{x + y} = e^{-2}\Leftrightarrow x + y = -2
\]
On résout :
\[
x + y = -2 \\
xy = -15
\]
C'est un système somme-produit :
\[
t^2 + 2t - 15 = 0\Leftrightarrow t = -5 \text{ ou } t = 3
\]
\(\boxed{S=\{ (-5, 3) ; (3, -5) \}}\)
3) Système :
\[
\begin{cases}
\ln x + \ln 4 = \ln 3 + \ln y \\
e^x = e^{x - 2}
\end{cases}
\]
La deuxième équation donne :
\[
e^x = e^{x - 2}\Leftrightarrow x = x - 2\Leftrightarrow 0 = -2\Leftrightarrow \text{Impossible.}
\]
\(\boxed{S=\varnothing}\)
EXERCICE 19
1) Développer \( A = e^{x-2} - (x + 1)(x - 2) \)
\[
A = e^{x-2} - (x^2 - 2x + x - 2) = e^{x-2} - (x^2 - x - 2) = e^{x-2} - x^2 + x + 2
\]
2) Résolution des équations
A) \( e^{3x} - 2e^{x+1} - e^x + 2 = 0 \)
Posons \( y = e^x \) :
\[
y^3 - 2e y - y + 2 = 0
\]
Cette équation semble complexe. Une autre approche est possible en factorisant :
\[
e^{3x} - e^x - 2e^{x+1} + 2 = 0\Leftrightarrow e^x(e^{2x} - 1) - 2(e^{x+1} - 1) = 0
\]
Une solution évidente est \( x = 0 \) :
\[
1 - 2e - 1 + 2 = 2 - 2e \neq 0
\]
Peut-être une erreur dans l'énoncé.
B) \( e^{x+2} = e^{x^2 + 4x} \)
Égalité des exposants :
\[
x + 2 = x^2 + 4x\Leftrightarrow x^2 + 3x - 2 = 0\Leftrightarrow x = \frac{-3 \pm \sqrt{9 + 8}}{2} = \frac{-3 \pm \sqrt{17}}{2}
\]
\(\boxed{S=\{\dfrac{-3 + \sqrt{17}}{2} ; \dfrac{-3 - \sqrt{17}}{2}\}}\)
EXERCICE 20
1) Racines de \( P(x) = x^2 + 4x - 5 \)
\[
x = \frac{-4 \pm \sqrt{16 + 20}}{2} = \frac{-4 \pm 6}{2}\Leftrightarrow x = 1 \text{ ou } x = -5
\]
2) Solutions de \( e^{2x} + 4e^x = 5 \)
Posons \( y = e^x \) :
\[
y^2 + 4y - 5 = 0\Leftrightarrow y = 1 \text{ ou } y = -5
\]
Seule \( y = 1 \) est possible :
\[
e^x = 1\Leftrightarrow x = 0
\]
\(\boxed{S=\{0\}}\)
3) Résolution des équations
A) \( e^{2x} + e^x - 2 = 0 \)
Posons \( y = e^x \) :
\[
y^2 + y - 2 = 0\Leftrightarrow y = 1 \text{ ou } y = -2
\]
Seule \( y = 1 \) est possible :
\[
x = 0
\]
\(\boxed{S=\{0\}}\)
B) \( e^{2x+1} + e^{x+1} - 2e = 0 \)
Factorisons \( e \) :
\[
e(e^{2x} + e^x - 2) = 0\Leftrightarrow e^{2x} + e^x - 2 = 0
\]
Comme ci-dessus, \( x = 0 \).
\(\boxed{S=\{0\}}\)
C) \( e^x - 2e^{-x} + 1 = 0 \)
Multiplions par \( e^x \) :
\[
e^{2x} + e^x - 2 = 0\Leftrightarrow x = 0
\]
\(\boxed{S=\{0\}}\)
EXERCICE 21
Simplification des expressions :
\[
A = \frac{e^x}{e^x} = \boxed{1}
\]
\[
B = e^x (1 + 2e^{-x}) = e^x + 2 = \boxed{e^x + 2}
\]
\[
C = \frac{e^{x+2}}{e^{x+1}} = e^{(x+2)-(x+1)} = e^1 = \boxed{e}
\]
\[
D = (e^x + e^{-x})^2 = e^{2x} + 2 + e^{-2x} = \boxed{e^{2x} + e^{-2x} + 2}
\]
\[
E = e^{2x} \cdot e^{-2x} = e^0 = \boxed{1}
\]
\[
F = e^{2x+1} \cdot e^{-2x} = e^{1} = \boxed{e}
\]
\[
G = \frac{e^{x+2}}{e^{x+1}} = e^1 = \boxed{e}
\]
\[
H = \frac{e^{x+1}}{(e^x)^2} = e^{x+1 - 2x} = e^{-x + 1} = \boxed{e^{1 - x}}
\]
EXERCICE 22
Nous allons démontrer les égalités suivantes pour tout réel \( x \).
1) Démontrer que \( \dfrac{e^x - 1}{e^x + 1} = \dfrac{1 - e^{-x}}{1 + e^{-x}} \)
Méthode :
Nous allons transformer le membre de droite pour montrer qu'il est égal au membre de gauche.
Calcul :
\[
\dfrac{1 - e^{-x}}{1 + e^{-x}} = \dfrac{1 - \dfrac{1}{e^x}}{1 + \dfrac{1}{e^x}} = \dfrac{\dfrac{e^x - 1}{e^x}}{\dfrac{e^x + 1}{e^x}} = \dfrac{e^x - 1}{e^x + 1}
\]
Conclusion :
Les deux membres sont égaux.
\[
\boxed{\dfrac{e^x - 1}{e^x + 1} = \dfrac{1 - e^{-x}}{1 + e^{-x}}}
\]
2) Démontrer que \( \dfrac{e^x - 1}{e^{2x}} = e^{-x} - e^{-2x} \)
Méthode :
Nous allons décomposer la fraction du membre de gauche.
Calcul :
\[
\dfrac{e^x - 1}{e^{2x}} = \dfrac{e^x}{e^{2x}} - \dfrac{1}{e^{2x}} = e^{-x} - e^{-2x}
\]
Conclusion :
Les deux membres sont égaux.
\[
\boxed{\dfrac{e^x - 1}{e^{2x}} = e^{-x} - e^{-2x}}
\]
3) Démontrer que \( \dfrac{e^{-x} + 1}{1 + e^x} = e^{-x} \)
Méthode :
Nous allons factoriser le numérateur et le dénominateur pour simplifier.
Calcul :
\[
\dfrac{e^{-x} + 1}{1 + e^x} = \dfrac{e^{-x}(1 + e^x)}{1 + e^x} = e^{-x}
\]
Remarque :
On a utilisé \( e^{-x} + 1 = e^{-x}(1 + e^x) \).
Conclusion :
Les deux membres sont égaux.
\[
\boxed{\dfrac{e^{-x} + 1}{1 + e^x} = e^{-x}}
\]
EXERCICE 23
Calcul des dérivées :
1) \( f(x) = e^{x^2 - x} \)
\[
f'(x) = (2x - 1)e^{x^2 - x}
\]
2) \( f(x) = e^{x^3 - 2x} \)
\[
f'(x) = (3x^2 - 2)e^{x^3 - 2x}
\]
3) \( f(x) = \frac{1 - e^{-x}}{1 - 2e^x} \)
Utilisons la formule \( \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2} \) :
\[
u = 1 - e^{-x}\Leftrightarrow u' = e^{-x} \\
v = 1 - 2e^x\Leftrightarrow v' = -2e^x \\
f'(x) = \frac{e^{-x}(1 - 2e^x) - (1 - e^{-x})(-2e^x)}{(1 - 2e^x)^2} = \frac{e^{-x} - 2 + 2e^x + 2e^x - 2}{(1 - 2e^x)^2} = \frac{e^{-x} + 4e^x - 4}{(1 - 2e^x)^2}
\]
4) \( f(x) = \frac{2e^x}{e^{x-1}} \)
Simplifions d'abord :
\[
f(x) = 2e^{x - (x - 1)} = 2e^1 = 2e\Leftrightarrow f'(x) = 0
\]
EXERCICE 24
1) $\lim\limits_{x \to +\infty} e^{-x} + 1$
- $e^{-x} = \frac{1}{e^x} \to 0$ quand $x \to +\infty$.
- Donc, $e^{-x} + 1 \to 0 + 1 = 1$.
$\boxed{\lim\limits_{x \to +\infty} e^{-x} + 1=1}$
2) $\lim\limits_{x \to 0} e^{-x} + 1$
- $e^{-x}$ est continue en $x = 0$, donc $e^{-0} = 1$.
- Donc, $e^{-x} + 1 \to 1 + 1 = 2$.
$\boxed{\lim\limits_{x \to 0} e^{-x} + 1=2}$
3) $\lim\limits_{x \to -\infty} e^{-x} + 1$
- Quand $x \to -\infty$, $-x \to +\infty$, donc $e^{-x} \to +\infty$.
- Donc, $e^{-x} + 1 \to +\infty$.
$\boxed{\lim\limits_{x \to -\infty} e^{-x} + 1=+\infty}$
4) $\lim\limits_{x \to +\infty} xe^{x}$
- $e^{x} \to +\infty$ et $x \to +\infty$, donc $xe^{x} \to +\infty$.
$\boxed{\lim\limits_{x \to +\infty} xe^{x}=+\infty}$
5) $\lim\limits_{x \to -\infty} xe^{-x}$
- Quand $x \to -\infty$, $-x \to +\infty$, donc $e^{-x} \to +\infty$.
- Mais $x \to -\infty$, donc on a une forme $-\infty \times +\infty = -\infty$.
$\boxed{\lim\limits_{x \to -\infty} xe^{-x}d=-\infty}$
6) $\lim\limits_{x \to -\infty} xe^{x}$
- $e^{x} \to 0$ quand $x \to -\infty$, et $x \to -\infty$.
- On a une forme $-\infty \times 0$, qui est indéterminée. On peut utiliser la règle de l'Hôpital ou un changement de variable :
- Posons $y = -x$, donc $x = -y$ et $y \to +\infty$ :
\[
xe^{x} = -ye^{-y} = -\frac{y}{e^{y}} \to 0 \quad \text{car } e^{y} \text{ domine } y.
\]
$\boxed{\lim\limits_{x \to -\infty} xe^{x}=0}$
7) $\lim\limits_{x \to -\infty} \dfrac{e^{2x}-1}{e^{x}+1}$
- Quand $x \to -\infty$, $e^{2x} = (e^{x})^2 \to 0$ et $e^{x} \to 0$.
- Donc, $\dfrac{e^{2x}-1}{e^{x}+1} \to \dfrac{0 - 1}{0 + 1} = -1$.
$\boxed{\lim\limits_{x \to -\infty} \dfrac{e^{2x}-1}{e^{x}+1}=-1}$
8) $\lim\limits_{x \to -\infty} \dfrac{1}{1+e^x}$
- $e^{x} \to 0$ quand $x \to -\infty$, donc $\dfrac{1}{1+0} = 1$.
$\boxed{\lim\limits_{x \to -\infty} \dfrac{1}{1+e^x}=1}$
9) $\lim\limits_{x \to +\infty} e^x + \dfrac{1}{x}$
- $e^{x} \to +\infty$ et $\dfrac{1}{x} \to 0$, donc $e^{x} + \dfrac{1}{x} \to +\infty$.
$\boxed{\lim\limits_{x \to +\infty} e^x + \dfrac{1}{x}=+\infty}$
10) $\lim\limits_{x \to +\infty} \dfrac{1}{1+e^{-2x}}$
- $e^{-2x} = \dfrac{1}{e^{2x}} \to 0$ quand $x \to +\infty$.
- Donc, $\dfrac{1}{1+0} = 1$.
$\boxed{\lim\limits_{x \to +\infty} \dfrac{1}{1+e^{-2x}}=1}$
11) $\lim\limits_{x \to +\infty} e^{2x} + e^{x} + 1$
- $e^{2x} = (e^{x})^2 \to +\infty$ et $e^{x} \to +\infty$, donc $e^{2x} + e^{x} + 1 \to +\infty$.
$\boxed{\lim\limits_{x \to +\infty} e^{2x} + e^{x} + 1=+\infty}$
12) $\lim\limits_{x \to +\infty} \dfrac{e^{x}+1}{2x}$
- $e^{x} \to +\infty$ et $x \to +\infty$, donc on a une forme $\dfrac{+\infty}{+\infty}$. Appliquons la règle de l'Hôpital :
\[
\lim_{x \to +\infty} \dfrac{e^{x}}{2} = +\infty.
\]
$\boxed{\lim\limits_{x \to +\infty} \dfrac{e^{x}+1}{2x}=+\infty}$
13) $\lim\limits_{x \to -\infty} (x^2 - 4x + 1)e^{x}$
- $x^2 - 4x + 1 \to +\infty$ et $e^{x} \to 0$ quand $x \to -\infty$. On a une forme $+\infty \times 0$, indéterminée.
- Posons $y = -x$, donc $x = -y$ et $y \to +\infty$ :
\[
(x^2 - 4x + 1)e^{x} = (y^2 + 4y + 1)e^{-y} = \dfrac{y^2 + 4y + 1}{e^{y}} \to 0 \quad \text{car } e^{y} \text{ domine tout polynôme}.
\]
$\boxed{\lim\limits_{x \to -\infty} (x^2 - 4x + 1)e^{x}=0}$
14) $\lim\limits_{x \to +\infty} e^{x} - x^2 - x$
- $e^{x} \to +\infty$ et $-x^2 - x \to -\infty$, donc on a une forme $+\infty - \infty$, indéterminée.
- On sait que $e^{x}$ croît plus vite que tout polynôme, donc $e^{x} - x^2 - x \to +\infty$.
$\boxed{\lim\limits_{x \to +\infty} e^{x} - x^2 - x=+\infty}$
EXERCICE 25
1) Domaine de définition et limites
- Domaine : \(\mathbb{R}\)
- Limite en \( +\infty \) :
\[
(1 - x)e^x + 1 \approx -x e^x \to -\infty
\]
- Limite en \( -\infty \) :
\[
e^x \to 0\Leftrightarrow (1 - x)e^x + 1 \to 1
\]
- Conclusion : La courbe a une asymptote horizontale \( y = 1 \) en \( -\infty \).
2) Dérivée et variations
\[
f'(x) = -e^x + (1 - x)e^x = -x e^x
\]
- Signe de \( f'(x) \) :
- Pour \( x < 0 \), \( f'(x) > 0 \) (croissante)
- Pour \( x > 0 \), \( f'(x) < 0 \) (décroissante)
- Tableau de variations :
- Maximum en \( x = 0 \), \( f(0) = 2 \)
3) Tangente à l'origine
La courbe coupe l'axe des ordonnées en \( x = 0 \), \( y = 2 \).
\[
f'(0) = 0\Leftrightarrow \text{Tangente horizontale } y = 2
\]
4) Branche infinie en \( -\infty \)
Asymptote horizontale \( y = 1 \).
5) Tracé de la courbe
- Passe par \( (0, 2) \)
- Croissante pour \( x < 0 \), décroissante pour \( x > 0 \)
- Asymptote \( y = 1 \) en \( -\infty \)
- Tend vers \( -\infty \) en \( +\infty \)
1)Domaine de définition et limites
On a :
$$
f(x) = (1 - x)e^x + 1
$$
Domaine de définition
Les termes sont définis ∀ $x \in \mathbb{R}$ (pas de division, pas de racine, exponentielle définie partout).
Donc :
$$
\boxed{\text{Dom}(f) = \mathbb{R}}
$$
Limites aux bornes
Quand $x \to -\infty$ :
$$
e^x \to 0^+, \quad 1 - x \to +\infty
$$
Donc :
$$
(1 - x)e^x \approx (+\infty) \cdot 0^+ \to 0
$$
car $e^x$ décroît bien plus vite que $x$.
Donc :
$$
\lim_{x \to -\infty} f(x) = 0 + 1 = 1
$$
Quand $x \to +\infty$ :
$$
e^x \to +\infty, \quad 1 - x \to -\infty
$$
Donc :
$$
(1 - x)e^x \approx (-\infty) \cdot (+\infty) = -\infty
$$
Donc :
$$
\lim_{x \to +\infty} f(x) = -\infty
$$
Conséquence pour la courbe $C_f$
À gauche : une asymptote horizontale $y = 1$ en $-\infty$.
À droite : $f(x) \to -\infty$, donc la courbe plonge.
2)Étude de la dérivée et variations
Dérivée :
$$
f'(x) = - e^x + (1 - x) e^x = - e^x +- e^x- xe^x = -x e^x
$$
Donc :
$$
\boxed{f'(x) = -x e^x}
$$
Signe de $f'(x)$
$e^x > 0$ ∀ $x$.
$-x$ change de signe en $x = 0$.
| x | −x | f′(x) |
|---|---|---|
| <0< | >0 | >0 (croissante) |
| =0 | 0 | 0 (extremum) |
| >0 | <0 | <0 (décroissante) |
Donc $f$ croît sur $]-\infty, 0]$, atteint un maximum en $x = 0$, puis décroît.
Valeur au maximum :
$$
f(0) = (1 - 0)e^0 + 1 = 1 \cdot 1 + 1 = 2
$$
Tableau de variations :
$$
\begin{array}{c|ccc|c}
x & -\infty & 0 & +\infty \\
\hline
f'(x) & + & 0 & - \\
\hline
f(x) & \nearrow & 2 & \searrow -\infty \\
\end{array}
$$
Donc :
$$
\boxed{\max f = 2 \text{ atteint en } x = 0}
$$
3)Tangente à l’axe des ordonnées
Le point d’intersection avec l’axe des ordonnées est :
$$
x = 0, \quad f(0) = 2
$$
Pente de la tangente :
$$
f'(0) = -0 \cdot e^0 = 0
$$
Équation de la tangente :
$$
y = f(0) + f'(0)(x - 0) = 2 + 0 \cdot (x) = 2
$$
Donc :
$$
\boxed{\text{Tangente horizontale } y = 2}
$$
4)Branche infinie en $-\infty$
Quand $x \to -\infty$ :
On a vu $f(x) \to 1$.
Regardons plus précisément :
$$
(1 - x)e^x = (-x + 1)e^x
$$
Or $e^x$ décroît beaucoup plus vite, donc :
$$
f(x) = 1 + o(1)
$$
Donc :
$$
\boxed{\text{Branche asymptotique horizontale } y = 1 \text{ en } -\infty}
$$
5)Tracé de la courbe
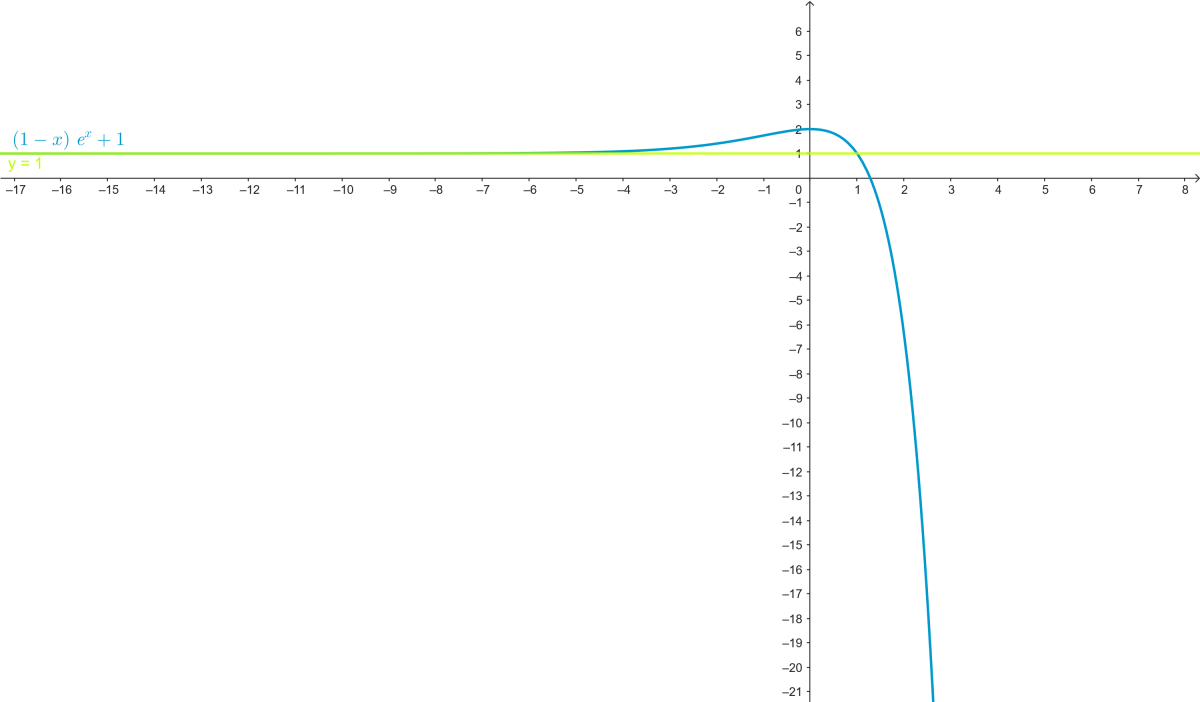

Ajouter un commentaire