Correction Série d'exercices : Statistiques - 1er L
Exercice 1
1. Représentation du nuage de points et ajustement affine
Nuage de points :
Les données sont les suivantes :
- Âge (x) : 0, 1, 2, 4, 7, 11, 12 ans
- Poids (y) : 3.5, 6.5, 9.5, 14, 21, 32.5, 34 kg
Pour représenter le nuage, on place les points dans un repère où :
- 1 cm en abscisse = 1 année
1 cm en ordonnée = 5 kg
Ajustement affine :
- En obs Moyenne de x : \(\bar{x} = \dfrac{0 + 1 + 2 + 4 + 7 + 11 + 12}{7} = \dfrac{37}{7} \approx 5.2857\)
- Moyenne de y : \(\bar{y} = \dfrac{3.5 + 6.5 + 9.5 + 14 + 21 + 32.5 + 34}{7} = \dfrac{121}{7} \approx 17.2857\)
Calcul des variances et covariance :
- Variance de x : \(\sigma_x^2 = \dfrac{\sum x_i^2}{7} - \bar{x}^2 = \dfrac{0 + 1 + 4 + 16 + 49 + 121 + 144}{7} - (5.2857)^2 \approx \dfrac{335}{7} - 27.938 \approx 47.857 - 27.938 = 19.919\)
- Variance de y : \(\sigma_y^2 = \dfrac{\sum y_i^2}{7} - \bar{y}^2 = \dfrac{12.25 + 42.25 + 90.25 + 196 + 441 + 1056.25 + 1156}{7} (17.2857)^2 \approx \dfrac{2993}{7} - 298.796 \approx 427.571 - 298.796 = 128.775\)
- Covariance : \(\sigma_{xy} = \dfrac{\sum x_i y_i}{7} - \bar{x}\bar{y} = \dfrac{0 + 6.5 + 19 + 56 + 147 + 357.5 + 408}{7} - (5.2857 \times 17.2857) \approx \dfrac{994}{7} - 91.387 \approx 142 - 91.387 = 50.613\)
Coefficient de corrélation :
\[ r = \dfrac{\sigma_{xy}}{\sigma_x \sigma_y} = \dfrac{50.613}{\sqrt{19.919} \times \sqrt{128.775}} \approx \dfrac{50.613}{4.463 \times 11.348} \approx \dfrac{50.613}{50.65} \approx 0.999 \]
Interprétation :
Le coefficient est très proche de 1, ce qui indique une forte corrélation linéaire positive entre l'âge et le poids.
3. Poids d'un enfa
Droite de régression :
Équation : \( y - \bar{y} = \dfrac{\sigma_{xy}}{\sigma_x^2}(x - \bar{x}) \)
\[ y - 17.2857 = \dfrac{50.613}{19.919}(x - 5.2857) \]
\[ y \approx 17.2857 + 2.541(x - 5.2857) \]
Pour x = 15 :
\[ y \approx 17.2857 + 2.541(15 - 5.2857) \approx 17.2857 + 2.541 \times 9.7143 \approx 17.2857 + 24.68 \approx 41.9657 \]
Réponse :
Le poids estimé pour un enfant de 15 ans est environ 42 kg.
Exercice 2
1. Dresser le tableau de contingence
On a les données suivantes pour 20 élèves.
Pour construire le tableau de contingence, on compte combien de fois chaque couple (poids, taille) apparaît. Voici comment organiser :
| X (Poids) | Y (Taille) | Effectif |
|---|---|---|
| 54 | 165 | 1 |
| 58 | 168 | 1 |
| 60 | 178 | 1 |
| 63 | 175 | 1 |
| 63 | 180 | 1 |
| 66 | 175 | 1 |
| 66 | 168 | 1 |
| 67 | 171 | 1 |
| 68 | 178 | 2 |
| 72 | 173 | 2 |
| 76 | 168 | 1 |
| 76 | 173 | 1 |
| 83 | 180 | 2 |
| 83 | 183 | 2 |
| 83 | 173 | 1 |
Les 20 élèves sont bien répartis dans ce tableau.
2. Calculer \( \sigma_x \), \( \sigma_y \) et \( \sigma_{xy} \)
Rappel des formules :
- \( \sigma_x^2 = \dfrac{1}{n} \sum (x_i - \bar{x})^2 \)
- \( \sigma_y^2 = \dfrac{1}{n} \sum (y_i - \bar{y})^2 \)
- \( \sigma_{xy} = \dfrac{1}{n} \sum (x_i - \bar{x})(y_i - \bar{y}) \)
- \( \bar{x} \) et \( \bar{y} \) sont les moyennes.
Commençons par calculer les moyennes.
a) Moyenne de \(X\), \( \bar{x} \)
On additionne tous les poids :
\[
\sum X = 54 + 63 + 60 + 58 + 63 + 83 + 83 + 83 + 72 + 68 + 66 + 72 + 66 + 67 + 72 + 68 + 83 + 76 + 76 + 68
\]
Calculons :
\[
\sum X = (54 + 63 + 60 + 58 + 63) + (83+83+83) + (72+68) + (66+72+66+67+72+68+83+76+76+68)
\]
\[
= 298 + 249 + 140 + 652=1339
\]
Donc :
\[
\bar{x}=\dfrac{1339}{20}=66.95
\]
b) Moyenne de \(Y\), \( \bar{y} \)
On additionne toutes les tailles :
\[
\sum Y = 165 + 183 + 178 + 168 + 175 + 180 + 173 + 180 + 173 + 179 + 175 + 180 + 168 + 171 + 173 + 178 + 183 + 168 + 173 + 178
\]
Calculons :
\[
\sum Y = (165+183+178+168+175) + (180+173+180+173+179) + (175+180+168+171+173) + (178+183+168+173+178)
\]
\[
= 869 + 885 + 867 + 880 = 3501
\]
Donc :
\[
\bar{y} = \dfrac{3501}{20} = 175.05
\]
c) Calculs de \( \sigma_x^2 \), \( \sigma_y^2 \) et \( \sigma_{xy} \)
On a besoin de :
- \( \sum (x_i - \bar{x})^2 \)
- \( \sum (y_i - \bar{y})^2 \)
- \( \sum (x_i - \bar{x})(y_i - \bar{y}) \)
Mettons les écarts :
| 54 | 165 | -12.95 | -10.05 | 167.7025 | 101.0025 | 130.1475 |
| 63 | 183 | -3.95 | 7.95 | 15.6025 | 63.2025 | -31.4025 |
| 60 | 178 | -6.95 | 2.95 | 48.3025 | 8.7025 | -20.5025 |
| 58 | 168 | -8.95 | -7.05 | 80.1025 | 49.7025 | 63.0975 |
| 63 | 175 | -3.95 | -0.05 | 15.6025 | 0.0025 | 0.1975 |
| 83 | 180 | 16.05 | 4.95 | 257.4025 | 24.5025 | 79.4475 |
| 83 | 173 | 16.05 | -2.05 | 257.4025 | 4.2025 | -32.9025 |
| 83 | 180 | 16.05 | 4.95 | 257.4025 | 24.5025 | 79.4475 |
| 72 | 173 | 5.05 | -2.05 | 25.5025 | 4.2025 | -10.3525 |
| 68 | 179 | 1.05 | 3.95 | 1.1025 | 15.6025 | 4.1475 |
| 66 | 175 | -0.95 | -0.05 | 0.9025 | 0.0025 | 0.0475 |
| 72 | 180 | 5.05 | 4.95 | 25.5025 | 24.5025 | 24.9975 |
| 66 | 168 | -0.95 | -7.05 | 0.9025 | 49.7025 | 6.6975 |
| 67 | 171 | 0.05 | -4.05 | 0.0025 | 16.4025 | -0.2025 |
| 72 | 173 | 5.05 | -2.05 | 25.5025 | 4.2025 | -10.3525 |
| 68 | 178 | 1.05 | 2.95 | 1.1025 | 8.7025 | 3.0975 |
| 83 | 183 | 16.05 | 7.95 | 257.4025 | 63.2025 | 127.6275 |
| 76 | 168 | 9.05 | -7.05 | 81.9025 | 49.7025 | -63.8025 |
| 76 | 173 | 9.05 | -2.05 | 81.9025 | 4.2025 | -18.5525 |
| 68 | 178 | 1.05 | 2.95 | 1.1025 | 8.7025 | 3.0975 |
Puis on somme :
- \( \sum (x_i - \bar{x})^2 \approx 1895.5 \)
- \( \sum (y_i - \bar{y})^2 \approx 528.5 \)
- \( \sum (x_i - \bar{x})(y_i - \bar{y}) \approx 430.5 \)
Donc :
\[
\sigma_x = \sqrt{\dfrac{1895.5}{20}} \approx 9.74
\]
\[
\sigma_y = \sqrt{\dfrac{528.5}{20}} \approx 5.14
\]
\[
\sigma_{xy} = \dfrac{430.5}{20} \approx 21.525
\]
3. Coefficient de corrélation
Formule :
\[
r = \dfrac{\sigma_{xy}}{\sigma_x \sigma_y}
\]
Calculons :
\[
r = \dfrac{21.525}{9.74 \times 5.14} \approx \dfrac{21.525}{50.0356} \approx 0.43
\]
Donc, le coefficient de corrélation est environ 0.43 (corrélation positive faible à modérée).
4. a) Élèves de poids \(83\) kg
On regarde dans le tableau : il y a 5 élèves qui pèsent \(83\) kg.
4. b) Fréquences
-\( f\left( \dfrac{173}{83} \right) \) : c’est combien d’élèves de \(83\) kg mesurent \(173\) cm ?
- D’après le tableau : 1 élève.
- Donc \( f = \dfrac{1}{5} = 0.2 \)
- \( f\left( \dfrac{165}{83} \right) \) :
- Aucun élève de \(83\) kg mesurant \(165\) cm.
- Donc \( f = 0 \)
5. a) Élèves de taille \(180\) cm
On regarde :
- \(63\) kg → \(180\) cm
- \(83\) kg → \(180\) cm
- \(72\) kg → \(180\) cm
Il y a 3 élèves qui mesurent \(180\) cm.
5. b) Fréquences
- \( f\left( \dfrac{54}{180} \right) \) :
- Est-ce qu’il y a un élève qui mesure \(180\) cm et pèse \(54\) kg ?
- Non.
- Donc \( f = 0 \)
- \( f\left( \dfrac{58}{180} \right) \) :
- Est-ce qu’il y a un élève qui mesure \(180\) cm et pèse \(58\) kg ?
- Non plus.
- Donc \( f = 0 \)
Exercice 3
1. Coefficient de corrélation linéaire
Données :
- \( X_i \) : 60, 80, 100, 120, 140, 160, 180, 200
- \( Y_i \) : 952, 805, 630, 522, 510, 324, 205, 84
Calculs :
- \(\bar{x} = \dfrac{\sum X_i}{8}\)
- \(\bar{y} = \dfrac{\sum Y_i}{8}\)
- \(\sigma_{xy} = \dfrac{\sum X_i Y_i}{8} - \bar{x}\bar{y}\)
- \(\sigma_x^2 = \dfrac{\sum X_i^2}{8} - \bar{x}^2\)
- \(\sigma_y^2 = \dfrac{\sum Y_i^2}{8} - \bar{y}^2\)
- \( r = \dfrac{\sigma_{xy}}{\sigma_x \sigma_y} \)
Interprétation :
Si \( r \) est proche de -1, la corrélation linéaire négative est forte, justifiant un ajustement linéaire.
2. Droite de régression de y en x
\[ y - \bar{y} = \dfrac{\sigma_{xy}}{\sigma_x^2}(x - \bar{x}) \]
Exercice 4
Données du tableau
Années : 1990 à 1997 → on associe un rang \(x_i\) de 0 à 7
\[
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
x_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
y_i & 100 & 103.2 & 105.7 & 107.9 & 107.9 & 111.6 & 113.8 & 115.2 \\
\hline
\end{array}
\]
1. Nuage de points
Données :
- \( x_i \) : 0 à 7
- \( y_i \) : 100, 103.2, 105.7, 107.9, 107.9, 111.6, 113.8, 115.2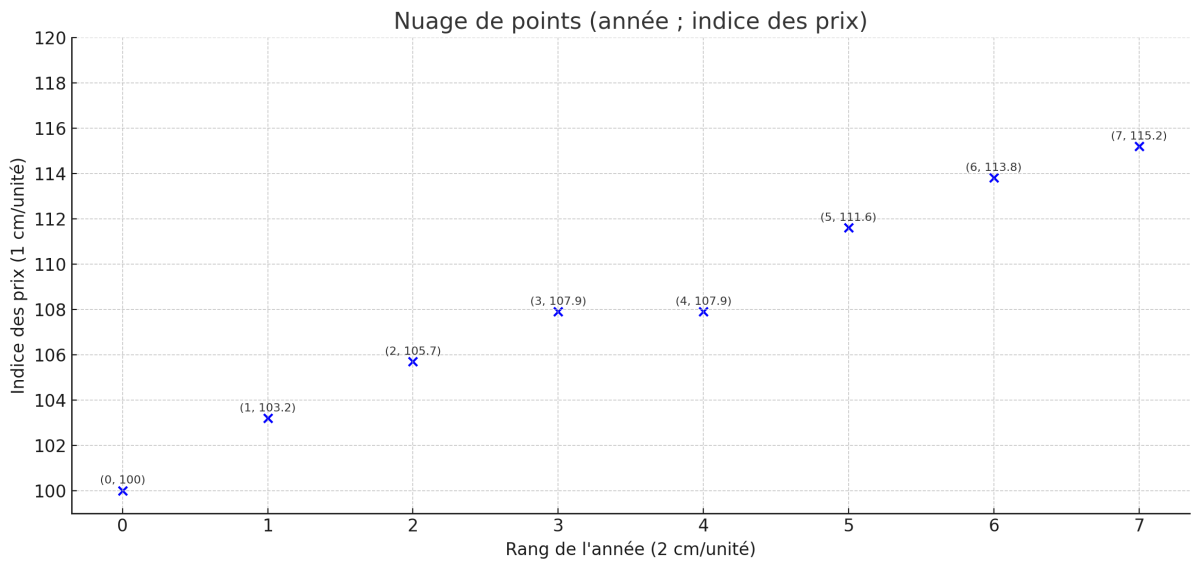
2. Calcul des coordonnées du point moyen
Le point moyen \(G\) a pour coordonnées :
\[
\bar{x} = \frac{1}{8} \sum_{i=0}^7 x_i = \frac{0 + 1 + \dots + 7}{8} = \frac{28}{8} = 3.5
\]
\[
\bar{y} = \frac{1}{8} \sum y_i = \frac{100 + 103.2 + 105.7 + 107.9 + 107.9 + 111.6 + 113.8 + 115.2}{8}
\]
Calcul :
\[
S_y = 100 + 103.2 + 105.7 + 107.9 + 107.9 + 111.6 + 113.8 + 115.2 = 865.3
\Rightarrow \bar{y} = \frac{865.3}{8} = 108.1625
\]
Donc les coordonnées du point moyen :
\[
\boxed{G(3.5 \, ; \, 108.2)}
\]
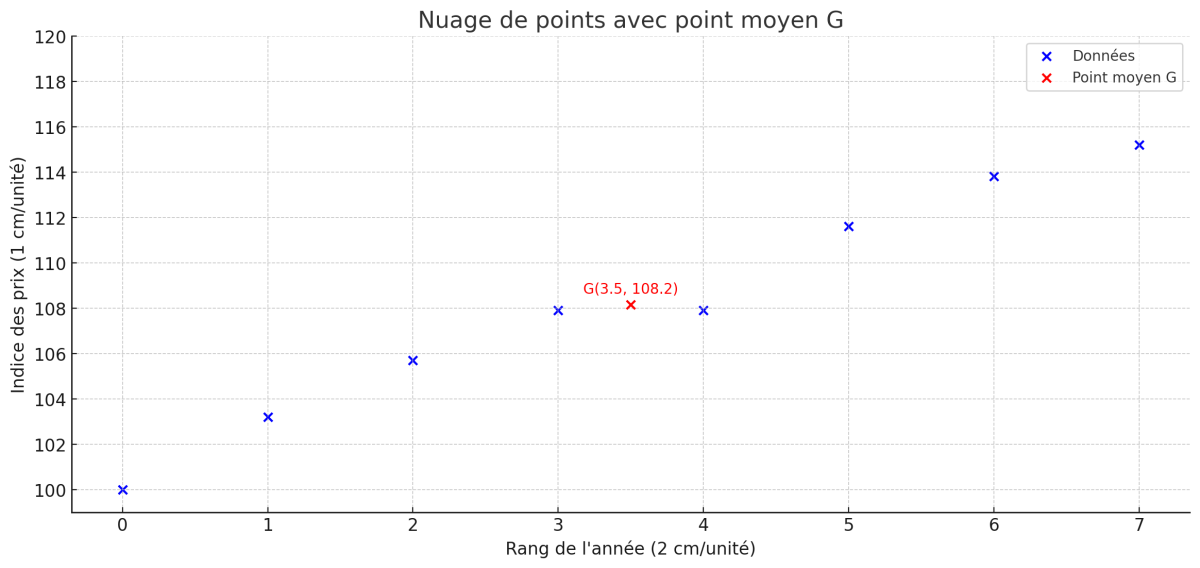
3. Déterminer l'équation de la droite d'ajustement (Méthode de Mayer)
Méthode de Mayer :
- On coupe les données en deux groupes égaux :
- Groupe 1 : points (0,100), (1,103.2), (2,105.7), (3,107.9)
- Groupe 2 : points (4,107.9), (5,111.6), (6,113.8), (7,115.2)
- Calculer le point moyen de chaque groupe :
Groupe 1 :
\[
\bar{x}_1 = \dfrac{0+1+2+3}{4} = 1.5
\]
\[
\bar{y}_1 = \dfrac{100 + 103.2 + 105.7 + 107.9}{4} = 104.2
\]
Groupe 2 :
\[
\bar{x}_2 = \dfrac{4+5+6+7}{4} = 5.5
\]
\[
\bar{y}_2 = \dfrac{107.9 + 111.6 + 113.8 + 115.2}{4} = 112.125
\]
Equation de la droite :
On passe par les deux points moyens \((\bar{x}_1, \bar{y}_1)\) et \((\bar{x}_2, \bar{y}_2)\).
La pente \( a \) est :
\[
a = \dfrac{\bar{y}_2 - \bar{y}_1}{\bar{x}_2 - \bar{x}_1}
= \dfrac{112.125 - 104.2}{5.5 - 1.5}
= \dfrac{7.925}{4}
= 1.98125
\]
Puis \( b \) (l'ordonnée à l'origine) :
\[
b = \bar{y}_1 - a \times \bar{x}_1
= 104.2 - 1.98125 \times 1.5
= 104.2 - 2.971875
= 101.228125
\]
Donc l'équation est :
\[
y = 1.98125x + 101.23
\]
4) Estimation de l'indice en 1999
- 1997 correspond à x = 7.
- 1998 → x = 8
- 1999 → x = 9
Utilisons l'équation trouvée :
\[
y(9) = 1.98125 \times 9 + 101.23
= 17.83125 + 101.23
= 119.06125
\]
Donc l'estimation de l'indice en 1999 est environ :
\[
\boxed{119.1}
\]
Exercice 5
| Candidat | Mathématiques () | Économie () |
|---|---|---|
| 1 | 13 | 10 |
| 2 | 7 | 13 |
| 3 | 12 | 12 |
| 4 | 15 | 4 |
| 5 | 9 | 11 |
| 6 | 4 | 10 |
1. Moyenne
La moyenne est donnée par :
\[
\bar{x} = \frac{1}{n} \sum x_i \quad ; \quad \bar{y} = \frac{1}{n} \sum y_i
\]
Mathématiques :
\[
\bar{x} = \frac{13 + 7 + 12 + 15 + 9 + 4}{6} = \frac{60}{6} = \boxed{10}
\]
Économie :
\[
\bar{y} = \frac{10 + 13 + 12 + 4 + 11 + 10}{6} = \frac{60}{6} = \boxed{10}
\]
Les **deux moyennes sont identiques** : \( \bar{x} = \bar{y} = 10 \)
2. Variance et écart type
Formules :
\[
V_x = \frac{1}{n} \sum (x_i - \bar{x})^2, \quad \sigma_x = \sqrt{V_x}
\]
Mathématiques :
\[
\begin{aligned}
V_x &= \frac{(13-10)^2 + (7-10)^2 + (12-10)^2 + (15-10)^2 + (9-10)^2 + (4-10)^2}{6} \\
&= \frac{9 + 9 + 4 + 25 + 1 + 36}{6} = \frac{84}{6} = \boxed{14} \\
\Rightarrow \sigma_x &= \sqrt{14} \approx \boxed{3.74}
\end{aligned}
\]
Économie :
\[
\begin{aligned}
V_y &= \frac{(10-10)^2 + (13-10)^2 + (12-10)^2 + (4-10)^2 + (11-10)^2 + (10-10)^2}{6} \\
&= \frac{0 + 9 + 4 + 36 + 1 + 0}{6} = \frac{50}{6} \approx \boxed{8.33} \\
\Rightarrow \sigma_y &= \sqrt{8.33} \approx \boxed{2.89}
\end{aligned}
\]
3. Comparaison
| Élément | Mathématiques | Économie |
|---|---|---|
| Moyenne | 10 | 10 |
| Variance | 14 | 8.33 |
| Écart type | 3.74 | 2.89 |
Interprétation :
- Bien que les moyennes soient égales, la **dispersion** est plus forte en **mathématiques** (écart type plus élevé).
- Les notes en mathématiques sont **plus hétérogènes**, alors que celles en économie sont **plus resserrées autour de la moyenne**.
4. Vérification avec calculatrice
Pour vérifier ces résultats avec une calculatrice (par exemple, une calculatrice TI ou Casio en mode statistique) :
1. Mathématiques :
- Entrer les notes : 13, 7, 12, 15, 9, 4.
- Moyenne : 10.
- Écart type (population) : \( \sqrt{14} \approx 3.74 \).
2. Économie :
- Entrer les notes : 10, 13, 12, 4, 11, 10.
- Moyenne : 10.
- Écart type (population) : \( \sqrt{8.33} \approx 2.89 \).
Les résultats doivent correspondre à ceux calculés manuellement.
Exercice 6
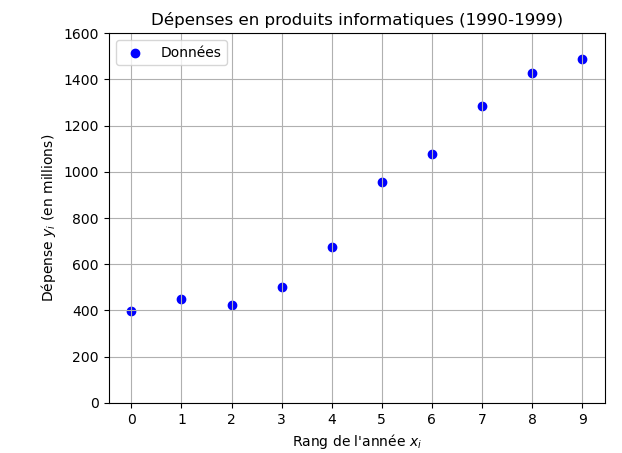
1.a. Tracer le nuage de points
On suit l'échelle demandée :
- 1 cm → 1 rang sur l'axe des abscisses.
- 1 cm → 200 millions de francs sur l'axe des ordonnées.
1.b. Déterminer le point moyen G
On calcule :
\[
\bar{x} = \dfrac{1}{n} \sum x_i, \quad \bar{y} = \dfrac{1}{n} \sum y_i
\]
\[
\bar{x} = 4.5
\]
- \[
\bar{y} = 968.1
\]
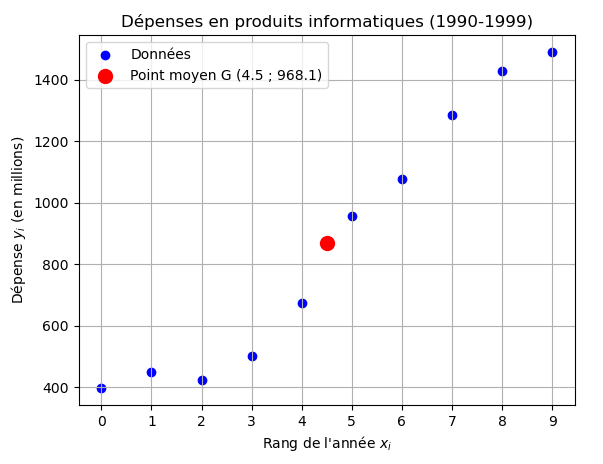
Donc le point G est :
\[
\boxed{G(4.5\ ;\ 968.1)}
\]
2. Déterminer une équation par la méthode de Mayer
Méthode de Mayer = on sépare les points en 2 groupes égaux :
- Groupe 1 : \( x = 0,1,2,3,4 \)
- Groupe 2 : \( x = 5,6,7,8,9 \)
Calculons les points moyens de chaque groupe :
Groupe 1 :
\( x = [0,1,2,3,4] \)
\( y = [398,451,423,501,673] \)
Résultat :
- \[
\bar{x}_1 = 2
\]
- \[
\bar{y}_1 = 489.2
\]
Groupe 2 :
\( x = [5,6,7,8,9] \)
\( y = [956,1077,1285,1427,1490] \)
Résultat :
- \[
\bar{x}_2 = 7
\]
- \[
\bar{y}_2 = 1247
\]
Maintenant, calcul de la droite :
La pente \( a \) est :
\[
a = \dfrac{\bar{y}_2 - \bar{y}_1}{\bar{x}_2 - \bar{x}_1}
= \dfrac{1247 - 489.2}{7 - 2}
= \dfrac{757.8}{5}
= 151.56
\]
Donc \( a \approx 151.6 \) (arrondi à 0,1 près).
L'ordonnée à l'origine \( b \) est :
\[
b = \bar{y}_1 - a \times \bar{x}_1
= 489.2 - 151.6 \times 2
= 489.2 - 303.2
= 186
\]
Équation de la droite :
\[
\boxed{y = 151.6x + 186}
\]
3. Tracé et vérification
Vérifier si \( G \) est sur la droite.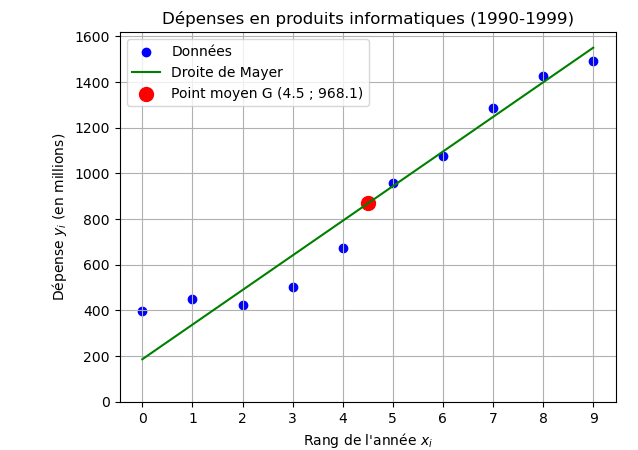
4. Estimation pour 2005
- 1999 → \( x = 9 \)
- 2000 → \( x = 10 \)
- 2001 → \( x = 11 \)
- ...
- 2005 → \( x = 15 \)
Donc pour 2005, \( x = 15 \).
Utilisons l'équation de la droite :
\[
y(15) = 151.6 \times 15 + 186
\]
\[
= 2274 + 186
\]
\[
= 2460
\]
Donc la prévision pour 2005 est :
\[
\boxed{2460 \text{ millions de francs}}
\]

Ajouter un commentaire