Correction Exercices d'entrainement types Bac : Statistiques - TL

Exercice 1

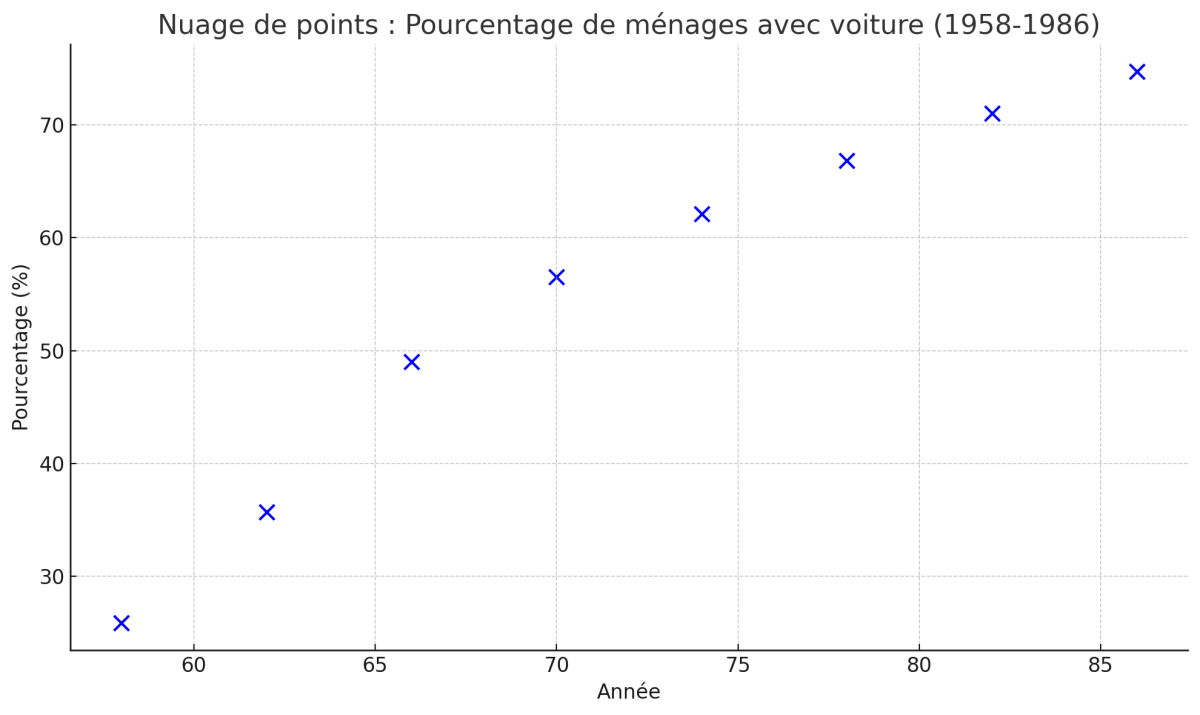
Le tableau donne l'évolution du pourcentage de ménages possédant au moins une voiture dans un pays A entre 1958 et 1986.

Année $x$	58	62	66	70	74	78	82	86
% voiture $y$	25.9	35.7	49	56.5	62.1	66.8	71	74.7

  1. Représenter le nuage de points

 Axe horizontal : $x$, l’année (utiliser 1 cm pour 2 ans ou centrer autour de 1970 pour limiter la largeur).
 Axe vertical : $y$, le pourcentage de ménages (échelle : 1 cm pour 5 % par exemple).
 Tracer les points $(58,\ 25.9),\ (62,\ 35.7),\dots,\ (86,\ 74.7)$

  2. Calculs statistiques

 a) Moyennes $\bar{X}$ et $\bar{Y}$

On calcule les sommes des $x$ et des $y$ :

$$
\sum x = 58 + 62 + 66 + 70 + 74 + 78 + 82 + 86 = 576 \Rightarrow \bar{X} = \frac{576}{8} = 72
$$

$$
\sum y = 25.9 + 35.7 + 49 + 56.5 + 62.1 + 66.8 + 71 + 74.7 = 441.7 \Rightarrow \bar{Y} = \frac{441.7}{8} = 55.21
$$

 b) Variances $V(X)$, $V(Y)$, Covariance $\text{cov}(X, Y)$

On construit un tableau :

$x$	$y$	$x - \bar{X}$	$y - \bar{Y}$	$(x - \bar{X})^2$	$(y - \bar{Y})^2$	$(x - \bar{X})(y - \bar{Y})$
58	25.9	-14	-29.31	196	858.36	4103.4
62	35.7	-10	-19.51	100	380.6	195.1
66	49	-6	-6.21	36	38.57	37.26
70	56.5	-2	1.29	4	1.66	-2.58
74	62.1	2	6.89	4	47.47	13.78
78	66.8	6	11.59	36	134.34	69.54
82	71	10	15.79	100	249.34	157.9
86	74.7	14	19.49	196	379.96	272.86
Totaux				672	2090.3	4847.3

Variance de X :

$$
V(X) = \frac{672}{8} = 84
$$

Variance de Y :

$$
V(Y) = \frac{2090.3}{8} \approx 261.29
$$

Covariance :

$$
\text{cov}(X, Y) = \frac{4847.3}{8} = 605.91
$$

  3. Droite de régression de $Y$ en $X$

Forme : $y = a x + b$, où :

 $a = \frac{\text{cov}(X, Y)}{V(X)} = \frac{605.91}{84} \approx 7.21$
 $b = \bar{Y} - a \bar{X} = 55.21 - 7.21 \times 72 = 55.21 - 519.12 = -463.91$

 Équation de la droite de régression :

$$
y = 7.21x - 463.91
$$

  4. Estimation pour l’année 2000

$x = 2000$ ? Attention ! Nos années sont notées sans les deux premiers chiffres (1958 → 58), donc 2000 correspond à x = 100

$$
y = 7.21 \times 100 - 463.91 = 721 - 463.91 = 257.09
$$

 Cela dépasse 100 %, donc il faut conclure que le modèle linéaire devient irréaliste à long terme. Il est probablement valide uniquement entre 1958 et 1986.

  Conclusion

 La proportion de ménages possédant au moins une voiture a fortement augmenté entre 1958 et 1986.
 La relation entre année et pourcentage est bien linéaire sur cette période.
 Le modèle de régression obtenu permet une estimation correcte sur une courte période, mais n’est pas fiable pour des projections trop lointaines comme l’an 2000.

Exercice 2 (Bac 2000, 1er groupe, série L1 et L'1)

On étudie ici l’évolution de la tension artérielle moyenne $Y$ en fonction de l’âge $X$ d’une population.

Âge $X$	36	42	48	54	60	66
Tension $Y$	11.8	14	12.6	15	15.5	15.1

  1. Représenter le nuage de points

Échelles :

 1/2 cm pour 1 an → 1 cm pour 2 ans
 3 cm pour 1 unité de tension

Coordonnées des points à tracer :

 (36, 11.8), (42, 14), (48, 12.6), (54, 15), (60, 15.5), (66, 15.1)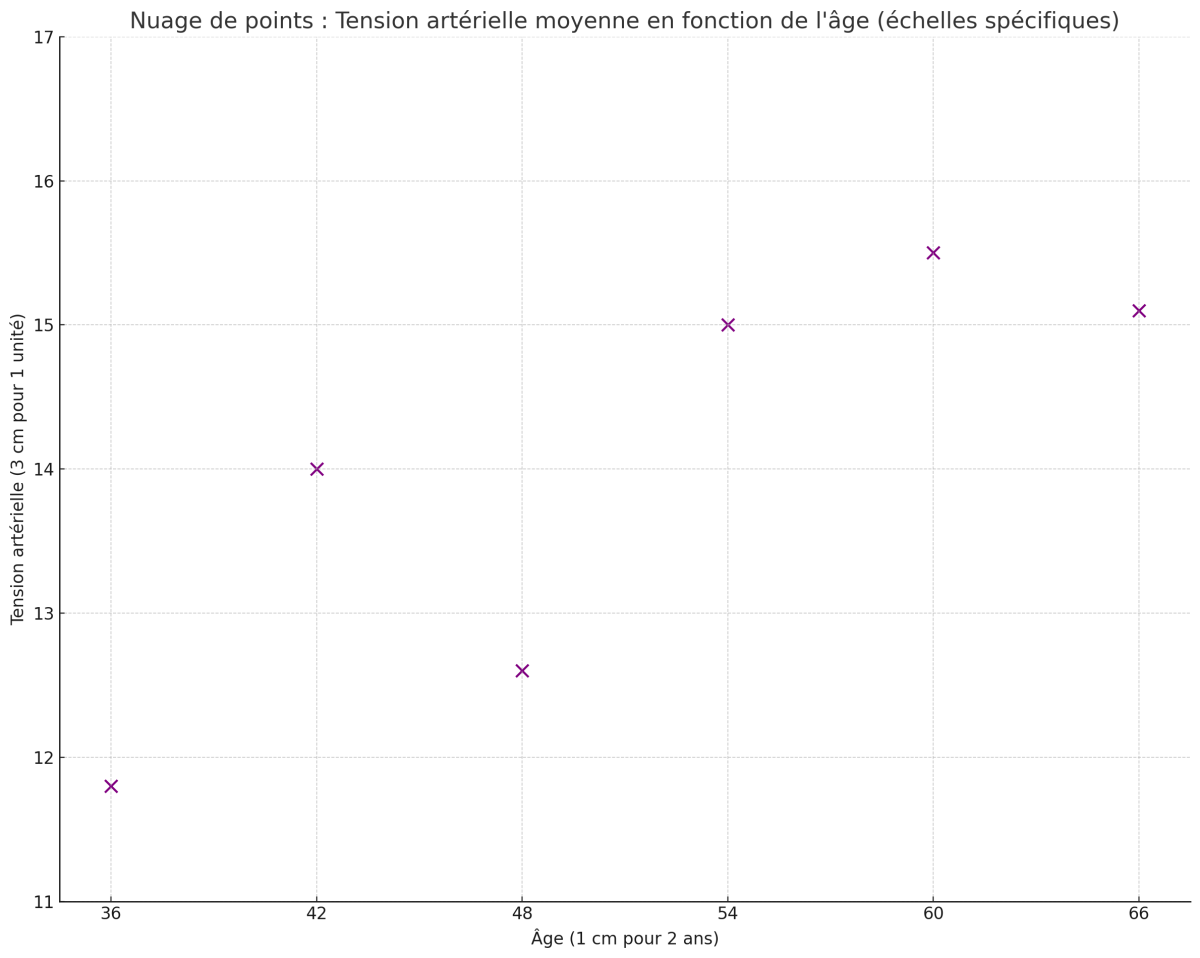

  2.a. Moyennes et variances

Données :

 $X = [36, 42, 48, 54, 60, 66]$
 $Y = [11.8, 14, 12.6, 15, 15.5, 15.1]$

 Calcul de la moyenne de $X$ :

$$
\bar{X} = \frac{36 + 42 + 48 + 54 + 60 + 66}{6} = \frac{306}{6} = 51
$$

 Moyenne de $Y$ :

$$
\bar{Y} = \frac{11.8 + 14 + 12.6 + 15 + 15.5 + 15.1}{6} = \frac{84}{6} = 14
$$

 Variance de $X$ :

$$
V(X) = \frac{1}{6} \sum (x_i - \bar{X})^2 = \frac{1}{6}[(36 - 51)^2 + \cdots + (66 - 51)^2]
$$

$$
V(X) = \frac{1}{6}[225 + 81 + 9 + 9 + 81 + 225] = \frac{630}{6} = 105
$$

 Variance de $Y$ :

$$
V(Y) = \frac{1}{6}[(11.8 - 14)^2 + \cdots + (15.1 - 14)^2]
= \frac{1}{6}[4.84 + 0 + 1.96 + 1 + 2.25 + 1.21] = \frac{11.26}{6} \approx 1.88
$$

  2.b. Coefficient de corrélation $r$

La covariance est :

$$
\text{cov}(X, Y) = \frac{1}{6} \sum (x_i - \bar{X})(y_i - \bar{Y})
$$

On fait le calcul détaillé :

$x_i$	$y_i$	$x_i - \bar{x}$	$y_i - \bar{y}$	Produit
60000	11	-6000	-7.25	43500
64000	17	-2000	-1.25	2500
68000	20	2000	1.75	3500
72000	25	6000	6.75	40500

$x$	$y$	$x - \bar{X}$	$y - \bar{Y}$	$(x - \bar{X})(y - \bar{Y})$
36	11.8	-15	-2.2	33.0
42	14	-9	0	0
48	12.6	-3	-1.4	4.2
54	15	3	1	3.0
60	15.5	9	1.5	13.5
66	15.1	15	1.1	16.5

$$
\text{cov}(X, Y) = \frac{33 + 0 + 4.2 + 3 + 13.5 + 16.5}{6} = \frac{70.2}{6} \approx 11.7
$$

Le coefficient de corrélation :

$$
r = \frac{\text{cov}(X, Y)}{\sqrt{V(X)} \cdot \sqrt{V(Y)}} = \frac{11.7}{\sqrt{105} \cdot \sqrt{1.88}} \approx \frac{11.7}{10.25 \cdot 1.37} \approx \frac{11.7}{14.05} \approx 0.83
$$

 Corrélation positive forte (car $r \approx 0.83$).

  3. Droite de régression de $Y$ en $X$

Forme : $y = a x + b$

 $a = \frac{\text{cov}(X, Y)}{V(X)} = \frac{11.7}{105} \approx 0.1114$
 $b = \bar{Y} - a \bar{X} = 14 - 0.1114 \cdot 51 \approx 14 - 5.68 = 8.32$

 Équation :

$$
y = 0.1114x + 8.32
$$

  4. Estimation pour une femme de $70$ ans

$$
x = 70 \Rightarrow y = 0.1114 \times 70 + 8.32 = 7.8 + 8.32 = 16.1
$$

 Estimation : La tension artérielle moyenne attendue est environ $16.1$.

Exercice 3 (Bac 2000, 1er groupe, L2)

On donne la série statistique suivante :

$X_i$	1.2	1.4	1.6	1.8	2
$Y_i$	13	12	14	16	$\alpha$

Et la droite de régression de $y$ en $x$ est donnée par :

$$
y = 9x + 0.6
$$

  1. Calcul de $\overline{X}$

$$
\overline{X} = \frac{1.2 + 1.4 + 1.6 + 1.8 + 2}{5} = \frac{8}{5} = 1.6
$$

  2. Exprimer $\overline{Y}$ en fonction de $\alpha$

$$
\overline{Y} = \frac{13 + 12 + 14 + 16 + \alpha}{5} = \frac{55 + \alpha}{5}
$$

  3. Déduire que $\alpha = 20$

L’idée ici est d’utiliser le fait que la droite de régression passe par le point moyen $G(\overline{X}, \overline{Y})$.

Or la droite est :

$$
y = 9x + 0.6
$$

Donc :

$$
\overline{Y} = 9\overline{X} + 0.6 = 9 \cdot 1.6 + 0.6 = 14.4 + 0.6 = 15
$$

Mais on a aussi :

$$
\overline{Y} = \frac{55 + \alpha}{5}
\Rightarrow \frac{55 + \alpha}{5} = 15 \Rightarrow 55 + \alpha = 75 \Rightarrow \alpha = 20
$$

 Donc, $\alpha = 20$

  4. Calcul du coefficient de corrélation linéaire

On utilise la formule :

$$
r = \frac{\text{cov}(X, Y)}{\sqrt{V(X)} \cdot \sqrt{V(Y)}}
$$

Ou bien on utilise le fait que la droite de régression est connue $y = 9x + 0.6$, donc :

 $a = 9$
 $r = a \cdot \frac{\sigma_X}{\sigma_Y} \Rightarrow r = \frac{\text{cov}(X,Y)}{\sigma_X \sigma_Y} = 9 \cdot \frac{\sigma_X^2}{\sigma_X \sigma_Y} = \frac{9 \sigma_X}{\sigma_Y}$

Nous devons donc calculer les variances ou les écarts-types.

On peut aussi utiliser une méthode directe avec tableau.

Données mises à jour :

$X$	$Y$
1.2	13
1.4	12
1.6	14
1.8	16
2.0	20

  5. Estimer $Y$ pour $X = 3.2$

À l’aide de la droite de régression :

$$
y = 9x + 0.6 \Rightarrow y = 9 \cdot 3.2 + 0.6 = 28.8 + 0.6 = 29.4
$$

Exercice 4

On note :

 $X$ : quantité de matières premières (en tonnes),
 $Y$ : chiffre d’affaires (en millions de francs),
 Les valeurs sont :
  $X = [0.9, 1.2, 0.6, 0.5, 1.4, 1.0]$,
  $Y = [37, 40 \text{ ou } 49, 33, 33, 41, 35]$

Le deuxième mois donne une ambiguïté : deux valeurs pour $Y$, soit 40 ou 49. On va faire le calcul deux fois si nécessaire.

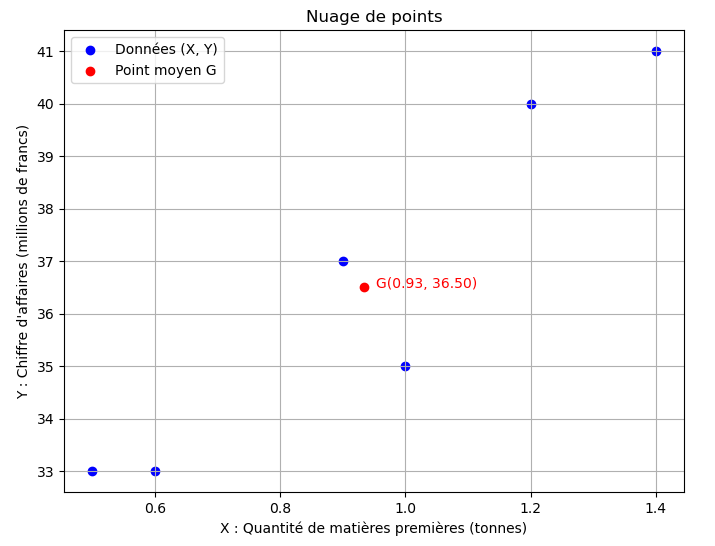
 1. Nuage de points et point moyen

Valeurs (cas avec $Y = 40$) :

$$
\begin{array}{|c|c|}
\hline
X & Y \\
\hline
0.9 & 37 \\
1.2 & 40 \\
0.6 & 33 \\
0.5 & 33 \\
1.4 & 41 \\
1.0 & 35 \\
\hline
\end{array}
$$

Point moyen $G(\bar{x}, \bar{y})$ :

$$
\bar{x} = \frac{0.9 + 1.2 + 0.6 + 0.5 + 1.4 + 1.0}{6} = \frac{5.6}{6} \approx 0.933
$$

$$
\bar{y} = \frac{37 + 40 + 33 + 33 + 41 + 35}{6} = \frac{219}{6} = 36.5
$$

 2.a. Covariance

Formule :

$$
\text{Cov}(X,Y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})
$$

On calcule :

$x_i$	$y_i$	$x_i - \bar{x}$	$y_i - \bar{y}$	Produit
0.9	37	-0.033	0.5	-0.0165
1.2	40	0.267	3.5	0.9345
0.6	33	-0.333	-3.5	1.1655
0.5	33	-0.433	-3.5	1.5155
1.4	41	0.467	4.5	2.1015
1.0	35	0.067	-1.5	-0.1005

Total : $\sum = 5.6$

$$
\text{Cov}(X,Y) = \frac{5.6}{6} \approx 0.933
$$

 2.b. Coefficient de corrélation

Formule :

$$
r = \frac{\text{Cov}(X,Y)}{\sigma_X \cdot \sigma_Y}
$$

On calcule :

 $\sigma_X^2 = \frac{1}{6} \sum (x_i - \bar{x})^2$
 $\sigma_Y^2 = \frac{1}{6} \sum (y_i - \bar{y})^2$

$$
\sum (x_i - \bar{x})^2 \approx 0.0011 + 0.0713 + 0.1109 + 0.1874 + 0.2180 + 0.0045 = 0.5932 \Rightarrow \sigma_X \approx \sqrt{0.0989} \approx 0.3146
$$

$$
\sum (y_i - \bar{y})^2 = 0.25 + 12.25 + 12.25 + 12.25 + 20.25 + 2.25 = 59.5 \Rightarrow \sigma_Y \approx \sqrt{9.9167} \approx 3.149 \Rightarrow r = \frac{0.933}{0.3146 \times 3.149} \approx \frac{0.933}{0.991} \approx 0.941
$$

 3. a. Équation de la droite de régression

Forme : $y = a x + b$

$$
a = \frac{\text{Cov}(X,Y)}{\sigma_X^2} = \frac{0.933}{0.0989} \approx 9.44
$$

$$
b = \bar{y} - a \bar{x} = 36.5 - 9.44 \cdot 0.933 \approx 36.5 - 8.81 \approx 27.69
$$

Donc :

$$
y = 9.44x + 27.69
$$

 4. Estimation de $X$ pour $Y = 40$

$$
40 = 9.44x + 27.69 \Rightarrow x = \frac{40 - 27.69}{9.44} \approx \frac{12.31}{9.44} \approx 1.30
$$

Donc, il faut environ 1.30 tonne de matières premières pour un chiffre d'affaires de 40 millions.

 Exercice 5

Données :

 $X =$ salaire proposé : $[60000, 64000, 68000, 72000]$
 $Y =$ candidatures : $[11, 17, 20, 25]$

 1. Nuage de points

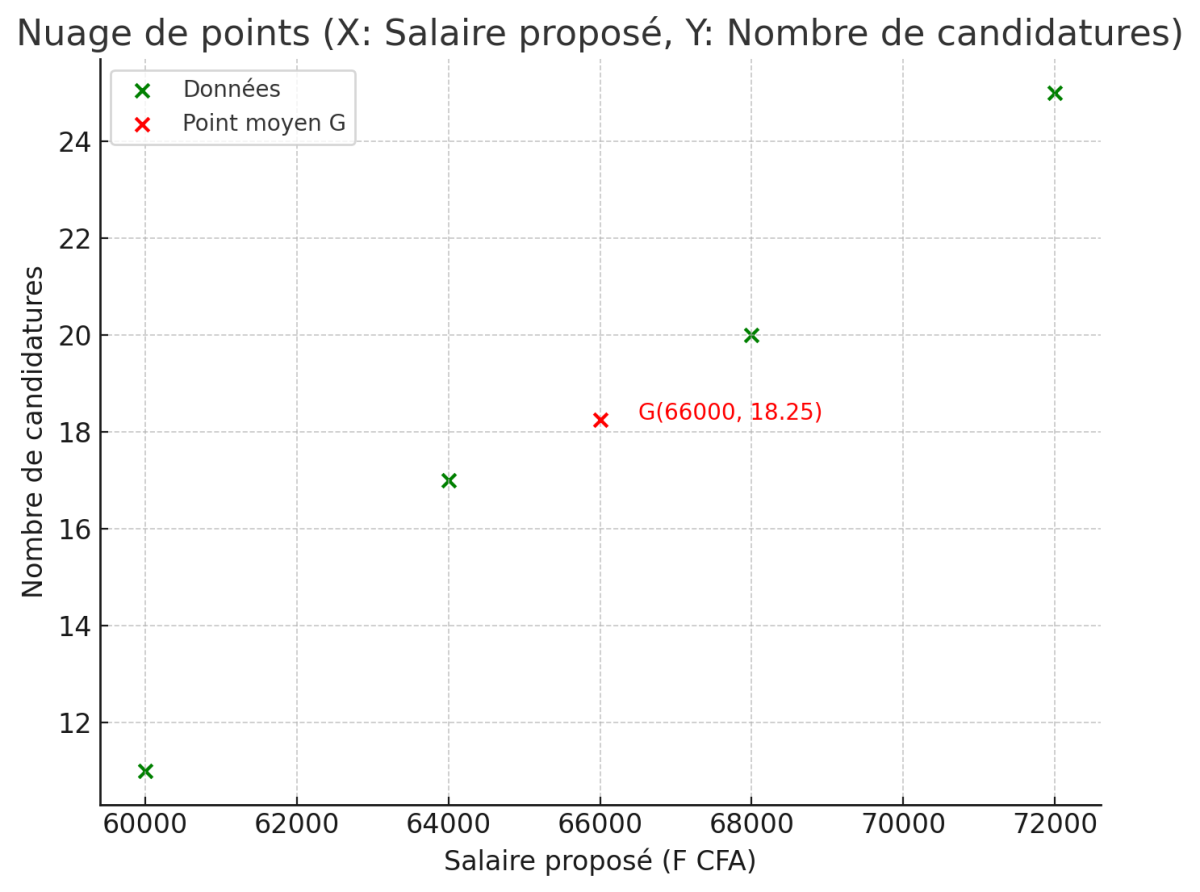
 2. Droite de régression de $Y$ en $X$

On centre les $X$ autour de leur moyenne pour simplifier :

 $\bar{X} = \frac{60000 + 64000 + 68000 + 72000}{4} = 66000$
 $\bar{Y} = \frac{11 + 17 + 20 + 25}{4} = 18.25$

$x_i$	$y_i$	$x_i - \bar{x}$	$y_i - \bar{y}$	Produit
60000	11	-6000	-7.25	43500
64000	17	-2000	-1.25	2500
68000	20	2000	1.75	3500
72000	25	6000	6.75	40500

$$
\text{Cov}(X,Y) = \frac{90000}{4} = 22500
$$

$$
\sigma_X^2 = \frac{1}{4}[(6000)^2 + (2000)^2 + (2000)^2 + (6000)^2] = \frac{88000000}{4} = 22000000
$$

$$
a = \frac{\text{Cov}(X,Y)}{\sigma_X^2} = \frac{22500}{22000000} = 0.001023
$$

$$
b = \bar{y} - a \cdot \bar{x} = 18.25 - 0.001023 \cdot 66000 \approx 18.25 - 67.52 = -49.27
$$

Donc, équation :

$$
y = 0.001023 x - 49.27
$$

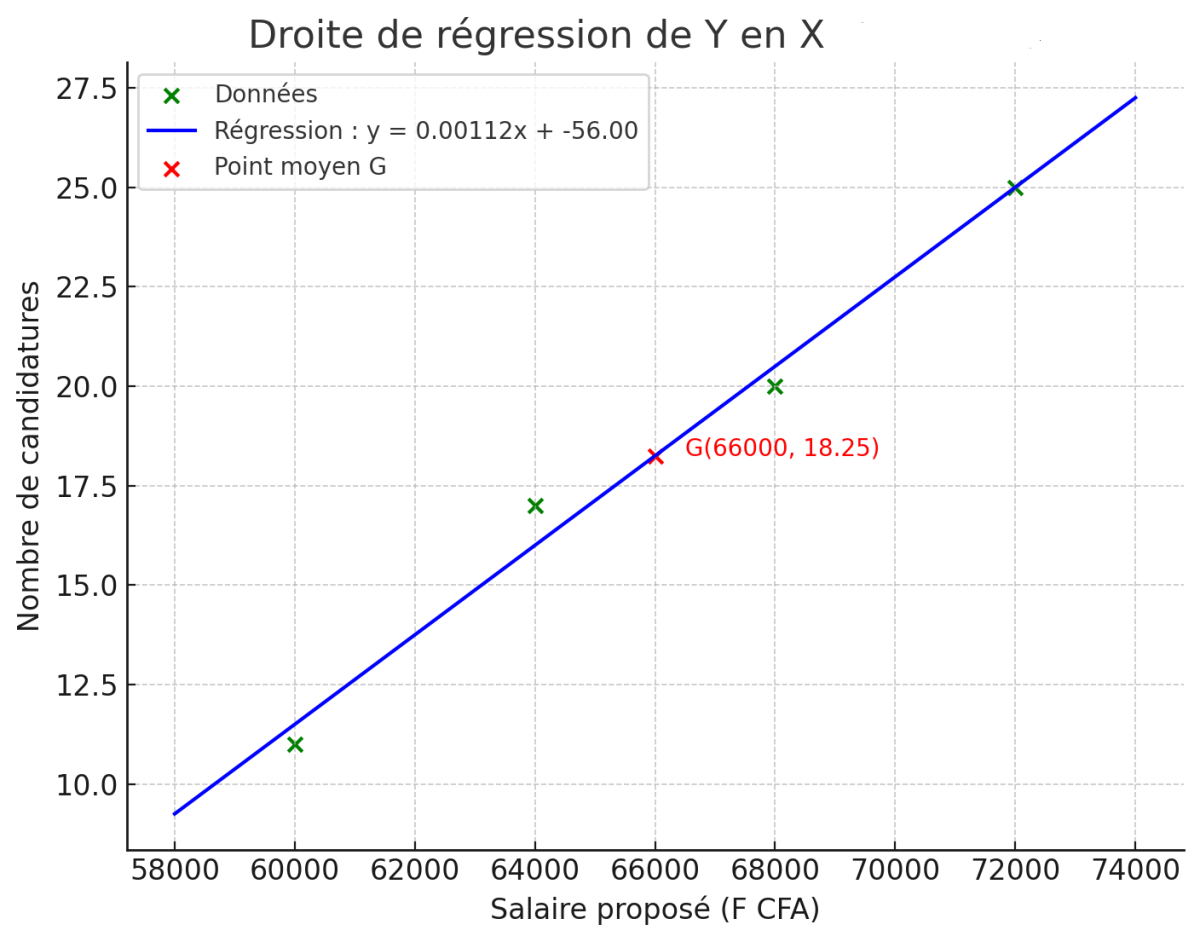
 3. Estimation du salaire pour 30 candidatures

$$
30 = 0.001023 x - 49.27 \Rightarrow x = \frac{30 + 49.27}{0.001023} \approx \frac{79.27}{0.001023} \approx 77533
$$

Il doit proposer environ 77 533 F CFA pour espérer 30 candidatures.