Concours Miss science - Épreuve de Mathématiques - 2nd S 2018

Première partie(1 point par réponse juste)

 

Chaque candidate répondra sur la feuille de réponses. 

 

Aucun point ne sera enlevé pour une réponse fausse ou une absence de réponse.

 

$\begin{array}{|l|l|} \hline \text{Questions}&\text{Réponses proposées}\\ \hline&a)\quad 0\leq a^{2}<9.\\ 1)\text{ Soit }a\text{ un réel tel que :}&b)\quad 9<a^{2}\leq 4.\\-3<a\leq 2.\text{ On a :}&c)\quad 0\leq a^{2}\leq 4\\ &d)\quad 4\leq a^{2}<9\\ \hline &a)\quad M\text{ barycentre de }{(A\;,2)\ ;\ (B\;,-1)}\\ 2)\text{ Soient }A\;,B\text{ et }M\text{ trois points }&b)\quad A\text{ barycentre de }{(M\;,1)\ ;\ (B\;,-2)}\\ \text{tels que : }\overrightarrow{AM}=2\overrightarrow{BA}\text{ On a : }&c)\quad B\text{ barycentre de }{(A\;,-3)\ ;\ (M\;,1)}\\ &d )\quad M\text{ barycentre de }{(A\;,1)\ ;\ (B\;,2)}\\ \hline 3)\text{ On considère dans }\mathbb{R}&a)\quad {5}\\\ \text{l'inéquation suivantes : }|x-5|<0&b)\quad\varnothing\\ \text{L'ensemble des solutions,}&c)\quad]-\infty\;\ 5[\\ \text{dans }\mathbb{R}\;,\text{ de cette inéquation}&d)\quad]5\ ;\ +\infty[\\ \hline &a)\quad\mathbb{R}\setminus{-1\ ;\ 1}\\ 4)\text{ La fonction }f\text{ définie par }f(x)=\sqrt{\dfrac{-x}{x^{2}+1}}&b)\quad]-\infty\ ;\ 0]\\ \text{a pour ensemble de définition :}&c)\quad]-\infty\;\ -1[\cup]-1\ ;\ 0]\\ &d)\quad\mathbb{R}\\\hline 5)\text{ Soit le tableau de variations ci-dessous}&a)\quad\text{comporte une seule erreur.}\\\text{d'une fonction }f\text{ définie sur }[-15\ ;\ 6]&b)\quad\text{ne comporte aucune erreur.}\\ \begin{array}{|c|lcccccr|} \hline x&-15&&-7&&-9&&6\\ \hline &&&-2&&&&0\\ f(x)&&\nearrow&&\searrow&&\nearrow&\\ &-1&&&&-3&& \\\hline\end{array}&c)\quad\text{ comporte deux erreurs }\\ \text{Ce tableau de variations :}&d)\quad\text{comporte trois erreurs.}\\\hline 6)\text{On donne la droite}\left(\mathbb{D_{1}}\right)&a)\quad\text{sont sécantes}\\ \text{d'équation }x+3y-1=0&b)\quad\text{Sont strictement parallèle }\\\text{et la droite }\left(\mathbb{D_{2}}\right)\text{d'équation :}&c\quad\text{Sont confondues :}\\ 3x+y+1=0\text{Ces deux droites :}&d)\quad\text{sont perpendiculaires.}\\ \hline &a)\quad\cos\left(\alpha\right)<0\ ;\ \sin\left(\alpha\right)<0.\\ 7)\text{On donne un angle }\alpha\text{ dont } &b)\quad\cos\left(\alpha\right)>0\ ;\ \sin\left(\alpha\right)<0\\ \text{la mesure principale est }\dfrac{3\pi}{5}\text{On a :}&c)\quad\cos\left(\alpha\right)<0\ ;\ \sin\left(\alpha\right)>0\\&d)\quad\cos\left(\alpha\right)>0\ ;\ \sin\left(\alpha\right)>0\\ \hline\end{array}$

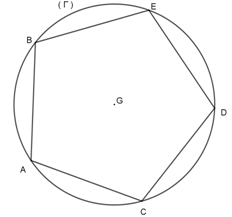
$8) \text{ Sur la figure ci-dessous},\ BACDE\text{ est un pentagone est un pentagone régulier inscrit}\\\text{dans le cercle}(\Gamma)\text{de centre}G\text{ et de rayon}10\,cm.\text{ La longueur de l'arc  est :}$

a) $\dfrac{2\pi}{5}\,cm\text{ régulier inscrit dans le cercle }$

b) $4\pi\,cm(I)\text{ de centre }G\text{ et de rayon }10\,cm$

c)  $12.56\,cm\text{ La longueur de l'arc }AB\text{est :}$

d) $1.256\,cm$

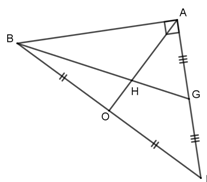
 $9)\text{ Sur la figure ci-contre,}BAK\text{ est un triangle rectangle isocèle en }A\\\text{ Les points}G\text{ et }O\text{ sont les milieux respectifs de}[AK]\text{ et } [BK].\text{Les droites}(OA)\text{ et } (BG)\\\text{ se coupent en } H.\text{ Le rapport de l’homothétie de centre } H\text{ qui transforme }O \text{ en }A \text{ est :}$

a) $-2$

$\begin{array}{|l|l|}\hline&a)\quad1\text{ est un zéro du polynôme }\\10)\text{ Soit le polynôme }P\text{ défini par }&b)\quad 0\text{ est un zéro du polynôme.}\\ P(x)=-3x^{3}+2x^{2}-x-6\text{ On a :}&c)\quad -1\text{ est un zéro du polynôme.}\\ &d)\quad -1\ ;\ 0\text{ et }1\text{ sont des zéros du polynôme}\\ \hline \end{array}$