Chapitre 5 : Suites numériques - TL

$\bullet\ $Reconnaitre une suite définie  par l'expression de son terme général ;
 
$\bullet\ $Reconnaitre une suite définie par un terme d'indice donné et une formule de récurrence ;
 
$\bullet\ $Calculer un terme d'une suite de rang donné ;

$\bullet\ $Étudier le sens de variation d'une suite ;

$\bullet\ $Étudier la convergence d'une suite ;
 
$\bullet\ $Définir et reconnaitre une suite arithmétique ou géométrique ;

$\bullet\ $Calculer le terme général d'une suite arithmétique ou géométrique en fonction du premier terme et de la raison ;

$\bullet\ $Calculer la somme des $n$ premiers termes d'une suite arithmétique ou géométrique ;  
 
$\bullet\ $Montrer qu'une suite géométrique est convergente ;

Prérequis :  

$\bullet\ $Suites numériques $\left(1^{er}L\right)$

Supports didactiques :  

$\bullet\ $Cours Faye-Ka-Mbengue ;

$\bullet\ $Hachette classique $1er$  $A1$ et $B$ ;

$\bullet\ $Programme sénégalais de mathématiques.
 

 
1. Activité

2. Définition et vocabulaire  

3. Des exemples de suite

a. Suites définies par une formule explicite

b. Suites définies par une formule de récurrence

4. Sens de variation d'une suite
 
5. Limites d'une suite
 

1. Définition

2. Expression du terme général  

3. Somme des n premiers termes

1. Définition

2. Expression du terme général

3. Somme des $n$ premiers termes

4. Convergence d'une suite géométrique

Déroulement du chapitre

La fiche ci-dessous donne dans l'ordre alphabétique des prénoms, les moyennes de $4$ élèves de la $TL'$ à l'issue la composition du $1er$  semestre.

$\begin{array}{|c|c|} \hline \text{Prénoms }&\text{Moyennes }\\ \hline \text{Awa }&12.\\ \hline \text{Baba }&8\\ \hline \text{Codou }&10\\ \hline \text{Dior }&11\\ \hline \end{array}$

a. En suivant l'ordre de cette fiche, écrire successivement sur une ligne la liste de ces
$4$ moyennes.
 
b. En considérant que la $1^{er}$  moyenne de cette liste occupe le rang $0$, préciser dans
l'ordre, les rangs des autres moyennes.

Solution

a. Dans l'ordre de la fiche ci-dessus, la liste de ces $4$ moyennes écrite successivement sur une ligne est : $12.5$ ;  $8$ ;  $10$ ;  $11$

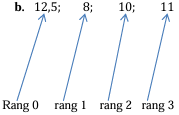
Exploitation
 
La liste ordonnée $12.5$ ;  $8$ ;  $10$ ; $11$ est une succession de nombres réels dite suite de nombres réels que l'on peut noter $u.$

Ainsi on peut écrire : $u$ ∶ $12.5$ ;  $8$ ;  $10$ ; $11$

Chaque élément de cette liste est appelé terme de la suite $u$ et peut être repéré dans la liste par son rang.

Pour noter un terme d'une suite, on écrit le nom de la suite et on met en indice le rang de
ce terme, ainsi le terme $12.5$ de rang $0$ de la suite u est noté $u_{0}=12.5$ ; le terme $8$ de rang $1$ est noté  $u_{1}=8$ ; le terme $10$ de rang $2$ est noté $u_{2}=10$ et le terme $11$ de rang est noté  $u_{3}=11$

2. Définition et vocabulaire et notation
Une suite numérique est une liste ordonnée de nombres réels.

Les éléments de cette suite sont
appelés termes de la suite et peuvent être  repérés dans la liste par leurs rangs.

En général, pour noter une suite, on utilise les lettres $u$ ou $v$ ou $w\ldots$

Pour une suite numérique $u$, le terme de rang $n$ $(n \text{est un entier naturel quelconque)}$ noté $u_{n}$ est aussi dit terme d'indice n et est appelé terme général de la suite.
 
Pour une suite numérique $u$, l'ensemble des indices (rangs) des termes de la suite est $\left\lbrace 0\ ;\ 1\ ;\ 2\ ;\ \ldots\right\rbrace$ ou un sous-ensemble de $\mathbb{R}$

Pour noter une suite numérique $u$ dont on connait l'ensemble des indices de ses termes alors on met le terme général $u_{n}$ entre parenthèses puis on précise l'ensemble des indices des termes de la suite.

Par exemple on peut avoir $\left(u_{n}\right)_{n\in\mathbb{N}}$ ou $\left(u_{n}\right)_{n\in\mathbb{N}^{\ast}}^{\ldots}\ldots$

$\bullet\ $Remarques

$\bullet\ $Lorsqu'on écrit ou $\left(u_{n}\right)_{n\in\mathbb{N}^{\ast}}$ alors le premier terme de cette suite est $u_{0}$, le second est $u_{1}\ldots$

$\bullet\ $Lorsqu'on écrit $\left(u_{n}\right)_{n\in\mathbb{N}^{\ast}}$ alors le premier terme de la suite est $u_{1}$, le second est $u_{2}$  

3.  Exemples de suites

a. Suites définies par une formule explicite :

Soit $I$ un sous-ensemble de $\mathbb{N}$

Une suite numérique $\left(u_{n}\right)n\in I$ peut être définie par une formule donnant directement le terme général $u_{n}$ en fonction de $n.$

Dans ce cas, on dit que la suite est définie par une formule explicite.

$\bullet\ $Exemple : Soit $\left(u_{n}\right)_{n\in\mathbb{N}}$

la suite numérique définie par $n_{n}=n^{2}$
 
Pour cette suite $u$, le terme d'indice $0$ est $u_{0}=1$ ; le terme d'indice $1$ est $u_{1}=1$ et le terme de d'indice $10$ est $u_{10}=101$ et le terme d'indice $n-1$ est $u_{n-1}=(n-1)^{2}+1=n^{2}-2n+2$
 
$\bullet\ $Exercice d'application

Soit $\left(u_{n}\right)_{n\in\mathbb{N}}$ la suite numérique définie par $u_{n}=n^{2}-n-2$

1. Calculer $u_{0}$ ; $u_{1}$ ; $u_{2}$ ; $u_{5}$ et $u_{8}$
 
2. Calculer $u_{n-1}$ et $u_{n+1}$ en fonction de $n$

b. Suites définies par une formule de récurrence

Une suite numérique $\left(u_{n}\right)_{n\in I}$ peut être définie en donnant la valeur de son premier terme puis en donnant un de ses termes généraux $u_{n+1}$ ou  $u_{n}$ ou $u_{n-1}\ldots$  

Dans ce cas, on dit que la suite est définie par une formule de récurrence.

Pour une telle suite, un terme d'indice donné ne peut être déterminé que si les termes qui le précèdent sont connus.  

$\bullet\ $Exemple : Soit $\left(u_{n}\right)_{\in\mathbb{N}}$

la suite numérique définie par : $\left\lbrace\begin{array}{rcl} u_{0}&=&2\\ u_{n+1}&=&3u_{n}+7 \end{array}\right.$

Le $1er$ terme de cette suite est $u_{0}=4$ ; $u_{1}=3u_{0}+7=13$ ; $u_{2}=3u_{1}+7=46$ et

$u_{3}=3u_{2}+7=145$

$\bullet\ $Exercice d'application

Soit $\left(u_{n}\right)_{n\in\mathbb{N}}$

la suite numérique définie par $\left\lbrace\begin{array}{rcl} u_{0}&=&-4\\ u_{n+1}&=&2u_{n}+5 \end{array}\right.$

Calculer $u_{1}$ ; $u_{2}$ ; $u_{3}$ ; $u_{4}$ et $u_{5}$  
 
4. Monotonie ou sens de variation d'une suite

$\bullet\ $Suite croissante
 
Une suite $\left(u_{n}\right)_{n\in\mathbb{N}}$

 est dite croissante si pour tout $n\in I$, on a : $u_{n+1}-u_{n}\geq 0$
 
$\bullet\ $Exemple : Soit la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ telle que : $u_{n}=\dfrac{n^{2}-n+2}{2}$

Montrons que la suite $\left(_{n}\right)_{n\in\mathbb{N}}$ est croissante.

$\bullet\ $Remarque : Si $u_{n+1}-u_{n}<0$ alors la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ est strictement croissante.

$\bullet\ $Suite décroissante
 
Une suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ est dite décroissante si pour tout $n\in I$, on a : $u_{n+1}-u_{n}\leq 0$
 
$\bullet\ $Remarque : Si $u_{n+1}-u_{n}<0$ alors la suite $\left(u_{n}\right)_{n\in I}$ est strictement décroissante.

$\bullet\ $Exemple : Soit la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ telle que : $u_{n}=-2n+5$
 
Montrons que la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ est strictement décroissante.

Étudier le sens de variation ou la monotonie d'une suite, c'est étudier si elle est croissante ou décroissante.

5. Limites d'une suite
 
On peut calculer la limite d'une suite $\left(u_{n}\right)_{n\in I}$  mais uniquement lorsque n tend vers +∞.
Ainsi, on a :  

$\bullet\ \lim\limits_{n\longleftarrow +\infty}n=+\infty$ ;

$\lim\limits_{n\longrightarrow\,+\infty}n^{2}=+\infty$ ;

$\lim\limits_{n\longrightarrow\,+\infty}n^{3}=+\infty$

$\bullet\ \lim\limits_{n\longrightarrow\,+\infty}\dfrac{1}{n}=0$ ;

$\lim\limits_{n\longrightarrow\,+\infty}\dfrac{1}{n^{2}}=0$ ;

$\lim\limits_{n\longrightarrow\,+\infty}\dfrac{1}{n^{3}}=0$
 
Les résultats sur les limites en $+\infty$ des fonctions restent valables avec les suites numériques.

Par exemple, on a :

$\bullet\ $ $\begin{array}{rcl} \lim\limits_{n\longrightarrow\,+\infty}\dfrac{-2n^{3}+n-1}{3n^{2}-1}&=&\lim\limits_{n\longrightarrow\,+\infty}\dfrac{-2n^{3}}{3n^{2}}\\&=&\lim\limits_{n\longrightarrow\,+\infty}\dfrac{-2n}{3}\\&=&-\infty \end{array}$

$\bullet\ $ $\begin{array}{rcl} \lim\limits_{n\longrightarrow\,+\infty}\dfrac{n^{3}+n-1}{3n^{3}-n+4}&=&\lim\limits_{n\longrightarrow\,+\infty}\dfrac{n^{3}}{3n^{3}}\\&=&\lim\limits_{n\longrightarrow\,+\infty}\dfrac{1}{3}\\&=&\dfrac{1}{3}\end{array}$

Remarque :

$\bullet\ $Si la limite d'une suite $\left(u_{n}\right)_{n\in I}$ quand $n$ tend vers $+\infty$ est un nombre réel l alors on dit que la suite $\left(u_{n}\right)_{n\in I}$ est convergente et on écrit $\lim\limits_{n\longrightarrow\,+\infty}u_{n}=I$

$\bullet\ $Si la limite d'une suite $\left(u_{n}\right)_{n\in I}$ quand tend vers $+\infty$ est $+\infty$ ou $-\infty$ alors on dit que la  suite $\left(u_{n}\right)_{n\in I}$ est divergente.

Une suite $\left(u_{n}\right)_{n\in I}$ est dite arithmétique s'il existe un réel constant $r$ tel que pour tout $n\in I$, $u_{n+1}-u_{n}=r$

Dans ce cas $r$ est dit raison de la suite $\left(u_{n}\right)_{n\in I}$

$\bullet\ $Exemple

Montrons que la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ précisera la raison.
 
telle que $u_{n}=2n+3$ est une suite arithmétique dont précisera la raison.

$\bullet\ $Exercice d'application

Montrons que la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ précisera la raison.
 
telle que $u_{n}=-n+5$ est une suite arithmétique dont précisera la raison.

2. Expression du terme général

Si $\left(u_{n}\right)_{n\in I}$ est une suite arithmétique de raison $r$ et de premier terme $u_{0}$ alors le terme général est égal à $u_{n}=u_{0}+r\times n$

$\bullet\ $Exemple
 
Donnons l'expression du terme général $u_{n}$ d'une suite arithmétique $\left(u_{n}\right)_{n\in\mathbb{N}}$ de premier terme $u_{0}=-5$ et de raison $3$
 
$\bullet\ $Propriété de premier terme  Si $u_{n}$ et $u_{p}$ sont deux termes quelconques d'une suite arithmétique de raison $r$ alors $u_{n}=u_{p}+r\times (n-p)$

$\bullet\ $Exercice d'application  

Donner l'expression du terme général $u_{n}$ d'une suite arithmétique $\left(u_{n}\right)_{n\in\mathbb{N}}$ et de raison $5.$

3. Somme des $n$ premiers termes
 
$\bullet\ $Nombre de termes d'une somme de termes consécutifs  de premier terme

Nombre de termes d'une somme de termes consécutifs= indice du $1er$ terme de la somme indice du dernier terme $+1.$

Par exemple, le nombre de termes de la somme des termes consécutifs $S=u_{0}+u_{1}+u_{2}+\ldots u_{p}$ est $+1$

$\bullet\ $Somme des $n$ premiers termes d'une suite arithmétique

La somme des $n$ premiers termes d'une suite arithmétique est donnée par :

nombre de termes de la $\times\dfrac{1er\text{terme +dernier terme}}{2}$

$\bullet\ $ Exemple
 
La suite $\left(u_{n}\right)_{n\in \mathbb{N}}$ telle que $u_{n}=2n+3$ est une suite arithmétique, calculons :

$S=u_{0}+u_{1}+u_{2}+\ldots u_{10}$   

4. Monotonie d'une suite arithmétique
 
Soit $\left(u_{n}\right)_{n\in\mathbb{N}}$ une suite arithmétique de raison $r$
 
$\bullet\ $Si $t>0$ alors la suite est strictement croissante.
 
$\bullet\ $Si $r<0$ alors la suite est strictement décroissante.
 

Une suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ est dite géométrique s'il existe un réel constant $q$ tel que pour tout $n\in I\;,\dfrac{u_{n+1}}{u_{n}}$

Dans ce cas $q$ est dit raison de la suite $\left(u_{n}\right)_{n\in I}$

$\bullet\ $Exemple

Montrons que la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ telle que $u_{n}=2^{n}$ est une suite géométrique dont précisera la raison.

$\bullet\ $Exercice d'application
 
Montrons que la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ telle que $u_{n}=3^{n}$ est une suite géométrique dont précisera la

2. Expression du terme général

$\bullet\ $Propriété :
 
Si $u_{n}$ et $u_{p}$ sont deux termes quelconques d'une suite géométrique de raison $q$ alors $u_{n}=q^{n-p}\times u_{p}$

$\bullet\ $Exemple
 
Donnons l'expression du terme général $u_{n}$ d'une suite géométrique $\left(u_{n}\right)_{n\in\mathbb{N}}$ de premier terme $u_{0}=2$ et de raison $3$
 
$\bullet\ $Exercice d'application
 
Donner l'expression du terme général $u_{n}$ d'une suite géométrique $\left(u_{n}\right)_{n\in\mathbb{N}}$ de premier terme $u_{1}=1$ et de raison $5.$
 
3. Somme des $n$ premiers termes d'une suite géométrique de premier terme

La somme des $n$ premiers termes d'une suite géométrique de raison $q$ est donnée par :

$1er$ terme de la somme $\times\dfrac{q^{\text{nombre de termes de la somme }-1}}{q-1}$

$\bullet\ $Exemple  

La suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ telle que $u_{n}=2^{n}$ est une suite géométrique de raison $2$, calculons :

$=u_{0}+u_{1}+u_{2}+\ldots u_{10}$
   
4. Convergence d'une suite géométrique

Si $\left(u_{n}\right)_{n\in I}$ est une suite géométrique de raison q telle que $-1< q<1$ alors la suite $\left(u_{n}\right)_{n\in I}$ est convergente et $\lim\limits_{n\longrightarrow\,+\infty}=u_{n}=0$

$\bullet\ $Exemple
 
Montrons que la suite $\left(u_{n}\right)_{n\in\mathbb{N}}$ telle que $u_{n}=\left(\dfrac{1}{2}\right)^{n}$ est géométrique puis étudions sa  convergence.