Calcul intégral - Tle

1) Définition et notation

Définition

Soit $f$ une fonction continue sur un intervalle $K$, $a$ et $b$ deux éléments de $K$ et $F$ une primitive de $f$ sur $K$.
Le nombre réel $F(b) - F(a)$ ne dépend pas de $F$. Il est appelé intégrale de} $a$ à $b$ de $f$.

Notation :

On note :
$$\int_a^b f(x)dx$$ et on lit « intégrale de $a$ à $b$ de $f(x)dx$  »

ou
$$[F(x)]_a^b$$ et on lit : « $F(x)$ pris entre $a$ et $b$ ».

Donc, on a :
$$\int_a^b f(x)dx = [F(x)]_a^b = F(b) - F(a)$$

Exercice :

Calcule les intégrales suivantes :
$$I = \int_0^1 x^2 dx ; \quad P = \int_0^1 z^2 dz ; \quad J = \int_3^1 \left(1 - \frac{1}{t}\right) dt$$

Solution :

• Considérons la fonction $f$ continue sur $[0; 1]$ et définie par :

    $$f(x) = x^2.$$
    Une primitive de $f$ sur $[0; 1]$ est la fonction $F$ définie par :
    $$F(x) = \frac{1}{3}x^3.$$
    Donc
    $$I = \int_0^1 x^2 dx = \left[ \frac{1}{3}x^3 \right]_0^1 = \frac{1}{3} \times 1^3 - 0 = \frac{1}{3}$$

•     $$P = I = \frac{1}{3} \text{ car la variable } z \text{ est muette.}$$

•   Considérons la fonction $f$ continue sur $[1; 3]$ et définie par

    $$f(t) = \left(1 - \frac{1}{t}\right).$$
    Une primitive de $f$ est la fonction $F$ définie par
    $$F(t) = t - \ln t.$$
    Donc :
    $$J = \int_3^1 \left(1 - \frac{1}{t}\right) dt = [t - \ln t]_3^1 = (1 - \ln 1) - (3 - \ln 3) = 1 - 3 + \ln 3 = -2 + \ln 3.$$

2) Interprétation graphique de l'intégrale d'une fonction continue et positive

  Propriété

Soit $f$ une fonction continue et positive sur un intervalle $[a; b]$ et $(C_f)$ sa courbe représentative dans le plan muni d'un repère orthogonal $(O, I, J)$.
$$\int_a^b f(x)dx$$ est l'aire $A$ en unités d'aire de la partie du plan limitée par la courbe $(C_f)$, l'axe (OI), les droites d'équations $x = a$ et $x = b$.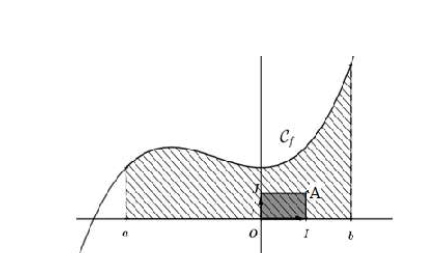

L’unité d’aire est l’aire du rectangle $OIAJ :1u. a = OI×O$
$$A=\int_a^b f(x)dx\text{ }u. a$$

Exercice de fixation :

Le plan est muni d’un repère orthogonal $(O; I; J)$.
Unités : 2 cm sur l’axe des abscisses et 3 cm sur l’axe des ordonnées.
On considère la fonction $f$ définie par : $f(x) = 2x + 1$. $f$ est continue et positive sur $[0; +\infty[$.
1) Calcule en cm², l’aire de la partie du plan limitée par la courbe de $f$, l’axe des abscisses et les droites d’équation $x = 0$ et $x = 5$.

Solution

1) L’unité d’aire en cm² est $2 \times 3$ cm².
$$\mathcal{A} = \left(\int_0^5 (2x + 1) dx\right) \times 6 \text{ cm}^2 = 6 \times [x^2 + x]_0^5 \text{ cm}^2 = 6 \times (25 + 5) \text{ cm}^2 = 180 \text{ cm}^2.$$

3) Calcul d’aire

a) Aire du plan limité par la courbe représentative d’une fonction, l’axe des abscisses et les droites d’équations $x = a$ et $x = b$

Propriétés

Le plan est muni d’un repère orthogonal $(O, I, J)$.
Soit $f$ une fonction continue positive sur $[a; b]$, $(C_f)$ sa courbe représentative.
$\mathcal{A}$ est l’aire de la partie du plan limitée par $(C_f)$, l’axe des abscisses $(OI)$, les droites d’équations $x = a$ et $x = b$.
On a $\mathcal{A} = \int_a^b f(x) dx$ u.a.

Exercice de fixation

Le plan est muni d’un repère orthogonal $(O, I, J)$. Unités : 2 cm sur l’axe des abscisses et 4 cm sur l’axe des ordonnées.
On considère la fonction $f$ définie par : $f(x) = x^2$. $f$ est continue et positive sur $\mathbb{R}$.
Calcule en cm², l’aire de la partie du plan limitée par la courbe de $f$, l’axe des abscisses et les droites d’équations : $x = 1$ et $x = 3$.

Solution

$$\mathcal{A} = \int_{1}^{3} x^{2} dx \, \text{en } (u.a).$$
L’unité d’aire en cm² est $2 \times 4$ cm², donc :
$$\mathcal{A} = \left(\int_{1}^{3} x^{2} dx\right) \times 8 \text{ cm}^2 = 8 \times \left[\frac{1}{3}x^{3}\right]_{1}^{3} \text{ cm}^2 = 8 \times \left(9 - \frac{1}{3}\right) \text{ cm}^2 = \frac{208}{3} \text{ cm}^2.$$

b) Aire du plan limitée par les courbes représentatives de deux fonctions et les droites d’équations $x = a$ et $x = b$

Propriétés

Le plan est muni d’un repère orthogonal $(O, I, J)$.
Soit $f$ et $g$ deux fonctions continues sur $[a; b]$ tel que : $f \geq g$ sur $[a; b]$ ; $(C_f)$ et $(C_g)$ leurs courbes représentatives respectives.
$\mathcal{A}$ est l’aire de la partie du plan limitée par $(C_f)$, $(C_g)$, les droites d’équations $x = a$ et $x = b$.
On a :
$$\mathcal{A} = \left(\int_{a}^{b} [f(x) - g(x)] dx\right) \text{ u.a.}$$

Exercice de fixation

Soit les fonctions $f$ et $g$ définies par : $f(x) = x + 2$ et $g(x) = x^{2}$. \\
On désigne par $(C_f)$ et $(C_g)$ les courbes représentatives de $f$ et $g$ dans le plan muni d’un repère orthonormé $(O, I, J)$. Unité graphique : 2 cm.
Calcule en cm², l’aire $\mathcal{A}$ de la partie du plan délimitée par $(C_f)$, $(C_g)$ et les droites d’équations : $x = -1$ et $x = 2$.

Solution
Étudions le signe de $g(x) - f(x)$.
$$g(x) - f(x) = x^{2} - x - 2 = (x + 1)(x - 2).$$

$$\begin{array}{|c|c|c|c|c|} \hline  x  & -\infty & -1 & &2 & +\infty \\ \hline  g(x) - f(x)  & + & 0 & - & 0 & + \\ \hline \end{array}$$

Donc pour tout $x \in [-1; 2]$, $g(x) - f(x) < 0$.
L’aire de la partie du plan délimitée par $(C_f)$, $(C_g)$ et les droites d’équations $x = -1$ et $x = 2$ est :
$$\int_{-1}^{2} (2 + x - x^{2}) dx \times 4 \text{ cm}^{2}.$$
Or :
$$\int_{-1}^{2} (2 + x - x^{2}) dx = \left[ 2x + \frac{1}{2}x^{2} - \frac{1}{3}x^{3} \right]_{-1}^{2} = \left(4 + 2 - \frac{8}{3}\right) - \left(-2 + \frac{1}{2} + \frac{1}{3}\right) = \frac{9}{2}.$$
L’aire cherchée est :
$$\mathcal{A} = \frac{9}{2} \times 4 \text{ cm}^{2} = 18 \text{ cm}^{2}.$$

c - Situation Complexe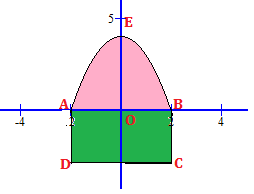
Un de vos camarades de classe rend visite à l’ancien professeur de mathématiques de son père à la retraite. Il remarque les formes géométriques particulières de la terrasse de celui-ci (voir figure ci-contre) : la partie en vert est délimitée par un rectangle de largeur 2 m et de longueur 4 m et la partie en rose est délimitée par une parabole et par un segment $[AB]$. Amusé par le regard de votre camarade, l’ancien professeur de mathématique le met au défi et lui demande de calculer l’aire totale de la terrasse en vue de lui donner une idée du coût des travaux de revêtement de cette terrasse.

Il lui présente le plan de la terrasse en précisant que pendant la construction, il a veillé à ce que la parabole qui apparaît dans le plan ait pour équation $y = -x^{2} + 4$ dans le repère orthonormé d’origine $O$ et d’unité 1 m, avec $A(-2,0)$ et $B(2,0)$.
Aide ce camarade à relever ce défi.

Solution
Pour calculer l’aire totale de la terrasse, on va :
    

•   calculer l’aire de la partie $ABCD$,
•   calculer l’aire $ABE$ délimitée par la parabole,
•    additionner les deux aires calculées précédemment.

1) Calculons l’aire $ABCD$ :
$$\text{Aire } ABCD = AB \times AD = 4 \times 2 = 8 \text{ m}^2.$$

2) Calculons l’aire $ABE$ :
$$\text{Aire } ABE = \int_{-2}^{2} (4 - x^{2}) dx = \left[4x - \frac{1}{3}x^{3}\right]_{-2}^{2} = \left(8 - \frac{8}{3}\right) - \left(-8 + \frac{8}{3}\right) = \frac{32}{3} \text{ m}^2.$$

3) L’aire de la terrasse est :
$$\frac{32}{3} + 8 = \frac{56}{3} \text{ m}^2 \approx 18,66 \text{ m}^2.$$