Baccalauréat S - Nouvelle Calédonie 2 décembre 2020
Exercice 1
Commun à tous les candidats
1. On considère l'équation (E):4z3−8z+8 ayant pour inconnue le nombre complexe z.
a. Démontrer que, pour tout nombre complexe z z3−4z2+8z=(z−2)(z2−2z+4)
b. Résoudre l'équation (E)
c. Écrire les solutions de l'équation (E) sous forme exponentielle.
On munit le plan complexe d'un repère orthonormé direct (O ; →u,→v)
Soit A, B, C et D les quatre points d'affixes respectives
zA=1+i√3
zB=2
zC=1−i√3
zD=1
Ces quatre points sont représentés dans la figure ci-dessous.
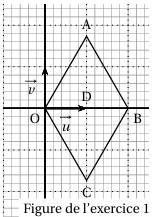
2. Quelle est la nature du quadrilatère OABC ?
Justifier.
3. Soit M le point d'affixe zM=74+i√34
a. Démontrer que les points A,M et B sont alignés.
b. Démontrer que le triangle DMB est rectangle
Exercice 2
Commun à tous les candidats
Le phaéton à bec rouge est un oiseau des régions intertropicales.
1. Lorsque le phaéton à bec rouge vit dans un environnement pollué, sa durée de vie, en an
née, est modélisée par une variable aléatoire X suivant une loi normale d'espérance μ inconnue et d'écart-type δ=0.95
a. On considère la variable aléatoire y définie par Y=X−μ0.95
Donner sans justification la loi suivie par la variable Y.
b. On sait que P(X≥4)=0.146
Démontrer que la valeur de μ arrondie à l'unité est 3
2. Lorsque le phaéton à bec rouge vit dans un environnement sain, sa durée de vie,en année,
est modélisée par une variable aléatoire Z.
Les courbes des fonctions de densité associées aux lois de X et de Z sont représentées sur l'ANNEXE à rendre avec la copie.
a. Quelle est la courbe de la fonction de densité associée à X ?
Justifier.
b. Sur l'ANNEXE à rendre avec la copie,hachurer la zone du plan correspondant à P(Z≥4)
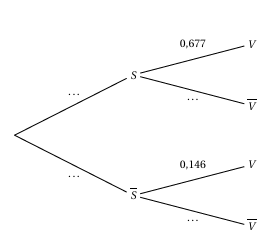
On admettra parla suite que P(Z≥4)=0.677
3. Une étude statistique portant sur une région donnée,a permis d'établir que 30% des phaétons à bec rouge vivent dans un environnement pollué; les autres vivent dans un environnement sain.
On choisit au hasard un phaéton à bec rouge vivant dans la région donnée.
On considère les évènements suivants :
∙ S :« le phaéton à bec rouge choisi vit dans un environnement sain » ;
∙ V :« le phaéton à bec rouge choisi a une durée de vie d'au moins 4 ans ».
a. Compléter l'arbre pondéré illustrant la situation sur l'ANNEXE à rendre avec la copie.
b. Déterminer P(V)
Arrondir le résultat au millième.
c. Sachant que le phaéton à bec rouge a une durée de vie d'au moins 4 ans, quelle est la probabilité qu'il vive dans un environnement sain ? Arrondir le résultat au millième.
Exercice 3
Commun à tous les candidats
Partie A
Soit g la fonction définie sur l'ensemble des nombres réels R, par g(x)=x2+x2+x+14+4(1+ex)2
On admet que la fonction g est dérivable sur R et on note g′ sa fonction dérivée.
1. Déterminer les limites de g en +∞ et en −∞
2. On admet que la fonction g′ est strictement croissante sur R et que g′(0)=0
Déterminer le signe de la fonction g′ sur R
3. Dresser le tableau de variations de la fonction g et calculer le minimum de la fonction g sur R
Partie B
Soit f la fonction définie sur R par : f(x)=3−21+ex
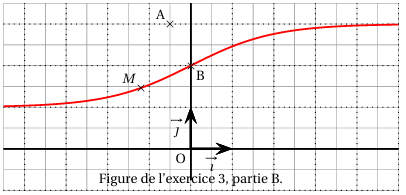
On désigne par Cf la courbe représentative de f dans un repère orthonormé (O ; →i,→j) , représentée dans la figure ci-dessous.
Soit A le point de coordonnées (−12 ; 3)
1. Démontrer que le point B(0 ; 2) appartient à Cf
2. Soit x un réel quelconque.
On note M le point de la courbe Cf de coordonnées (x ; f(x))
Démontrer que AM2=g(x)
3. On admet que la distance AM est minimale si et seulement si AM2 est minimal.
Déterminer les coordonnées du point de la courbe Cf tel que la distance AM est minimale.
4. On admet que la fonction f est dérivable sur R et on note f′ sa fonction dérivée.
a. Calculer f′(x) pour tout réel x
b. Soit T la tangente à la courbe Cf au point B
Démontrer que l'équation réduite de T est y=x2+2
5. Démontrer que la droite T est perpendiculaire à la droite (AB)
Exercice 4
Candidats n'ayant pas suivi l'enseignement de spécialité
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse, en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte.
Une absence de réponse n'est pas pénalisée.
1. Affirmation 1: L'équation (3lnx−5)(ex+4)=0 admet exactement deux solutions réelles.
2. On considère la suite (un) définie par u0=2 et,pour tout entier naturel n, un+1=2un−5n+6
Affirmation 2: Pour tout entier naturel n, un=n2+12
3. On considère la suite (un) définie, pour tout entier naturel n, par un=n2+12
Affirmation 3: La suite (un) est géométrique.
4. Dans un repère de l'espace,soit d la droite passant par le point A(−3 ; 7 ; −12) et de vecteur directeur →u(1 ; −2 ; 5)
Soit d′ la droite ayant pour représentation paramétrique
{x=2t−1y=−4t+3,t∈Rz=10t−2
Affirmation 4: Les droites d et d′ sont confondues.
5. On considère un cube ABCDEFGH, L'espace est muni du repère orthonormé (A ; →AB,→AD,→AE)
Une représentation paramétrique de la droite (AG) est
{x=ty=tt∈Rz=t
On considère un point M de la droite (AG)
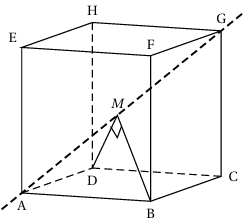
Affirmation 5: Il ya exactement deux positions du point M sur la droite (AG) telles que les droites (MB) et (MD) soient orthogonales.
Exercice 4
Candidats ayant suivi l'enseignement de spécialité
Pour chacune des affirmations suivantes,indiquer si elle est vraie ou fausse,en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas
prise en compte.
Une absence de réponse n'est pas pénalisée.
1. Affirmation 1: Les solutions de l'équation 7x−12y=5, où x et y sont des entiers relatifs, sont les couples (−1+12k ; −1+7k) où k décrit l'ensemble des entiers relatifs.
2. Affirmation 2 : Pour tout entier naturel n,le reste de la division euclidienne de 4+3×15n par 3 est égal à 1
3. Affirmation 3 : L'équation n(2n2−3n+5)=3, où n est un entier naturel,admet au moins une solution.
4. Soit t un nombre réel.
On pose A=(t32t−t)
Affirmation 4 : Il n'existe aucune valeur du réel t pour laquelle A2=(1001)
5. On considère les matrices
A=(01−1−12−11−12) et I3=(100010001)
Affirmation 5:Pour tout entier n≥2, An=(22−1)A+(2−2n)I3
Exercice 2 question 2
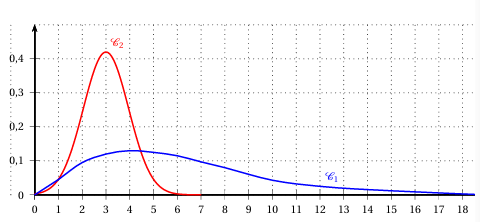
Exercice 2 question 3

Ajouter un commentaire