Baccalauréat S métropole-la réunion 11 septembre 2020

On considère la fonction $f$ définie sur $\mathbb{R}$ par : $$f(x)=\dfrac{2\mathrm{e}^{x}}{\mathrm{e}^{x}+1}$$

On donne ci-dessous la courbe représentative $\mathbb{C}$ de la fonction $f$ dans un repère orthonormé.

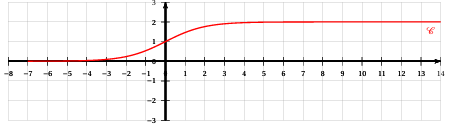
 1. Calculer la limite de la fonction $f$ en moins l'infini et interpréter graphiquement le résultat.
 
2. Montrer que la droite d'équation $y=2$ est asymptote horizontale à la courbe $\mathbb{C}$

3. Calculer $f'(x)$, $f'$ étant la fonction dérivée de $f$, et vérifier que pour tout nombre réel $x$ on a $$f'(x)=\dfrac{f(x)}{\mathrm{e}^{x}+1}$$

4. Montrer que la fonction $f$ est croissante sur $\mathbb{R}$

5. Montrer que la courbe $\mathbb{C}$ passe par le point $I(0\ ;\ 1)$ et que sa tangente en ce point a pour coefficient directeur $0.5$

Une entreprise souhaite fabriquer de façon automatisé des flûtes (verres à pied) de forme allongée de contenance $12.5\,cl$

Chaque flûte est composée de deux parties comme sur l'illustration ci-dessous :

un pied, en verre plein, et un contenant de $12.5\,cl$

À l'aide de la fonction $f$ définie dans la partie $A$, le fabricant modélise le profil du contenant de la flûte de la manière décrite ci-dessous.

Soit $A$ un point de $\mathbb{C}$ d'abscisse a strictement positive.

La rotation autour de l'axe des abscisses appliquée à la partie de C limitée parles points $I$ et $A$ engendre une surface modélisant le contenant de la flûte en prenant pour unité $1\,cm$

Ainsi $x$ et $f(x)$ représente des longueurs en centimètres et l'objectif de cette partie est de déterminer la valeur de a pour que le volume du contenant soit égal à $12.5\,cl$

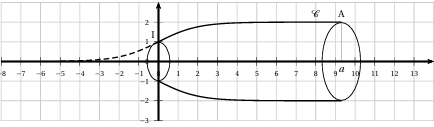
Une unité représente $1\,cm$

La valeur de $\alpha$ utilisée sur le graphique ci-dessus ne correspond pas à la valeur cherchée

Le réel a étant strictement positif, on admet que le volume $V(\alpha)$ de ce solide en $cm^{3}$ est donné par la formule: $$V(\alpha)=\pi\int_{0}^{\alpha}(f(x))^{2}dx$$

1. Vérifier, pour tout nombre réel $x\geq 0$, l'égalité :
$$(f(x))^{2}=4\left(\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}\right)+\dfrac{-\mathrm{e}^{x}}{\left(\mathrm{e}^{x}+1\right)}^{2}$$

 2. Déterminer une primitive sur $\mathbb{R}$ de chacune des fonctions : $$g\ :\ x\longmapsto\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}\text{ et }h\ :\ x\longmapsto\dfrac{-\mathrm{e}^{x}}{\left(\mathrm{e}+1\right)^{2}}$$

3. En déduire que pour tout réel $\alpha>0$ :
$$V(\alpha)=4\pi\left[\ln\left(\dfrac{\mathrm{e}^{\alpha}+1}{2}\right)+\dfrac{1}{\mathrm{e}^{\alpha}+1}-\dfrac{1}{2}\right]$$

4. Déterminer, à l'aide de la calculatrice, une valeur approchée de a à $0.1$ près, sachant qu'une flûte doit contenir $12.5\,cl$, c'est-à-dire $125\,cm^{3}.$

Aucune justification n'est attendue.

Un client commande un lot de $400$ flûtes de $12.5\,cl$ et constate que $13$ d'entre elles ne sont pas conformes aux caractéristiques annoncées par le fabricant.

Le responsable des ventes lui avait pourtant affirmé que $98\%$ des flûtes vendues par l'entreprise étaient conformes.

Le lot de ce client permet-t-il, aux risques de $5\%$, de mettre en doute l'affirmation du responsable?

Une machine fabrique des boules destinées à un jeu de hasard.

La masse en grammes, de chacune de ces boules peut-être modélisée par une variable aléatoire $M$ suivant une loi normale d'espérance $52$ et d'écart type $\delta$

Les boules dont la masse est comprise entre $51$ et $53$ grammes sont dites conformes.

1. Avec les réglages initiaux de la machine on a $\delta=0.437$

Dans ces conditions, calculer la probabilité qu'une boule fabriquée par cette machine soit conforme.
 
On donnera une valeur approchée à $10^{-1}$ près du résultat.

2. On considère que la machine est correctement réglée si au moins $99\%$ des boules qu'elle fabrique sont conformes.

Déterminer une valeur approchée de la plus grande valeur de $\delta$ qui permet d'affirmer que la machine est correctement réglée.

 
La pesée des boules se fait sur des balances électroniques de précision.

Chaque jour, on vérifie que la balance n'est pas déréglée.

La durée, en jour, d'utilisation de ces balances avant dérèglement est modélisée par une variable aléatoire $T$ qui suit une loi exponentielle de paramètre $\lambda$

La courbe représentative de la fonction densité de cette variable aléatoire $T$ est donnée ci-dessous.

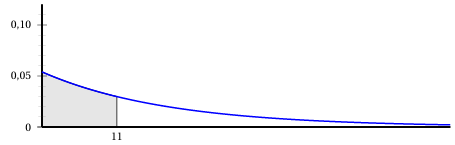
1.a. Par lecture graphique, donner un encadrement de $\lambda$ d'amplitude $0.01$

b. L'aire du domaine grisé, en unité d'aire,est égale à $0.45.$

Déterminer la valeur exacte de $\lambda$

Dans la suite, on prendra $\lambda=0.054$

2. Déterminer, à un jour près, la durée moyenne d'utilisation d'une balance sans qu'elle ne se dérègle.

3. Une balance est mise en service le $1er$ janvier $2020.$

Elle fonctionne sans se dérégler du $1er$ au $20$ janvier inclus.

Déterminer la probabilité qu'elle fonctionne sans se dérégler jusqu'au $31$ janvier inclus.
 

On dis pose de deux urnes $U$ et $V$ contenant des boules fabriquées comme précédemment. Sur chacune des boules est inscrit l'un des nombres $-1$, $1$, ou $2.$

L'urne $U$ contient une boule portant le nombre $1$ et trois boules portant le nombre $-1$

L'urne $V$ contient une boule portant le nombre $1$ et trois boules portant le nombre $2.$

On considère un jeu lequel chaque partie se déroule de la manière suivante: dans un premier temps

on tire au hasard une boule dans l'urne $U$,on note $x$ le nombre inscrit sur cette boule puis on la met dans l'urne $V.$
 
Dans un deuxième temps, on tire au hasard une boule dans l'urne $V$ et on note $y$ le nombre inscrit sur cette boule.

On considère les évènements suivants:

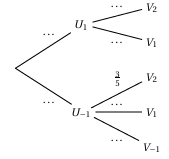
$\bullet\ U_{1}$ :« on tire une boule portant le nombre $1$ dans l'urne $U$,c'est-à-dire $x=1$ » ;

$\bullet\ U_{-1}$ : « on tire une boule portant le nombre $-1$ dans l'urne $U$ c'est-à-dire $x=-1$ » ;

$\bullet\ V_{2}$ :« on tire une boule portant le nombre $2$ dans l'urne $V$ c'est-à-dire $y=2$ » ;

$\bullet\ V_{1}$ : « on tire une boule portant le nombre $1$ dans l'urne $V$ c'est-à-dire $y=1$ » ;

$\bullet\ V_{-1}$ : « on tire une boule portant le nombre $-1$ dans l'urne $V$ »,c'est-à-dire $y=-1$ ».

1.Recopier et compléter l'arbre pondéré représenté ci-dessous

2. Dans ce jeu, à chaque partie on associe le nombre complexe $z=1+iy$

Calculer les probabilités des évènements suivants.

Les réponses seront justifiées.

a. $A\ :\ <<z=-1-i>>$ ;

b. $B$ : « $z$ est solution de l'équation $t^{2}+2t+5=0$ » ;

c. $C$ :« Dans le plan complexe rapporté à un repère orthonormal $\left(O\ ;\ \vec{u}\;,\vec{v}\right)$ le point $M$ d'affixe $z$ appartient au disque de centre $0$ et de rayon 2 ».

3. Lors d'une partie,on obtient le nombre $1$sur chacune des boules tirées.

Montrer que le nombre complexe $z$ associé à cette partie vérifie $z^{2020}=-2^{1010}$

Commun à tous les candidats

L'objectif de cet exercice est de déterminer les position relative de différents objets de l'espace

L'espace est rapporté à un repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\;,\vec{k}\right)$

On considère les points $A51\ ;\ 1\ ;\ 4)\ ;\ B(4\ ;\ 2\ ;\ 5)\ ;\ (3\ ;\ 0\ ;\ -2)$ et $J(1\ ;\ 4\ ;\ 2)$

On note: $\mathbb{P}$  le plan passant par les points $A$,$B$ et $C$ ;
 
$\bullet\ \mathbb{D}$ la droite passant par le point $J$ et de vecteur directeur $\vec{u}\begin{pmatrix} 1\\ 1\\ 3 \end{pmatrix}$

1. Position relative de $\mathbb{P}$ et de $\mathbb{D}$

a. Montrer que le vecteur $\vec{n}\begin{pmatrix} 1\\ -4\\ 1 \end{pmatrix}$ est normal à $\mathbb{P}$

b. Déterminer une équation cartésienne du plan $\mathbb{P}$

c. Montrer que $\mathbb{D}$ est parallèle à $\mathbb{P}$

On rappelle que, un point $I$ et un nombre réel strictement positif $r$ étant donnés, la sphère de centre $I$ et de rayon $r$ est l'ensemble des points $M$ de l'espace vérifiant $IM=r$

On considère le point $I(1\ ;\ 9\ ;\ 0)$ et on appelle $\mathbb{S}$ la sphère de centre $I$ et de rayon $6.$

2. Position relative de $\mathbb{P}$ et de $\mathbb{S}$

a. Montrer que la droite $\delta$ passant par $I$ et orthogonale au plan $P$ coupe ce plan $P$ au point $H(3\ ;\ 1\ ;\ 2)$

b. Calculer la distance $IH$

On admet que pour tout point $M$ du plan $\mathbb{P}$ on a $IM\geq IH$

c. Le plan $\mathbb{P}$ coupe-t-il la sphère $\mathbb{S}$ ?

Justifier la réponse

3. Position relative de $\mathbb{D}$ et de $\mathbb{S}$

a. Déterminer une représentation paramétrique de la droite $\mathbb{D}$

b. Montrer qu'un point $M$ de coordonnées $(x\ ;\ y\ ;\ z)$ appartient à la sphère $\mathbb{S}$ si et seulement si : $$(x-1)_{2}+(y-9)^{2}+z^{2}=36$$

c. Montrer que la droite $\mathbb{D}$ coupe la sphère en deux points distincts.

On ne cherchera pas à déterminer les coordonnées de ses points.

Pour les candidats n'ayant pas suivi l'enseignement de spécialité
 
On considère la suite $\left(U_{n}\right)$ définie, pour tout entier naturel non nul $n$, par : $$u_{n}=\dfrac{n(n+2)}{(n+1)^{2}}$$

La suite $\left(v_{n}\right)$ est définie par :

$v_{1}=u_{1}$, $v_{2}=u_{1}\times u2$ et pour tout entier naturel $n\geq 3$, $v_{n}=u_{1}\times u_{2}\times \ldots\times u_{n}=v_{n-1}\times u_{n}$

1. Vérifier que l'on a $v_{2}=\dfrac{2}{3}$ puis calculer $v_{3}$

2. On considère l'algorithme incomplet ci-dessous.

$\begin{array}{|c|} \hline \text{Algorithme }\\ \hline 1. V\longleftarrow 1\\ 2.\text{ pour }i\text{ varient de }1\text{ à }n\\ 3. U\longlefttarrow \dfrac{\ldots(\ldots+2)}{(\ldots+1)^{2}}\\ 4. V\longleftarrow\ldots\\ 5.\text{Fin pour}\\ \hline \end{arry}$

Recopier et compléter sur la copie cet algorithme afin que, après son exécution, la variable $V$ contiennent la valeur $v_{n}$ où $n$ est un nombre entier naturel non nul définie par l'utilisateur.

Aucune justification n'est attendue.

3. a. Montrer que,pour tout entier naturel non nul $n$, $u_{n}=1-\dfrac{1}{((n+1)^{2}}$

b. Montrer que,pour tout entier naturel non nul $n$, $0<u_{n}<1$

a. Montrer que la suite $\left(v_{n}\right)$ est décroissante

b. Justifier que la suite $\left(v_{n}\right)$ est convergente (on ne demande pas de calculer sa limite).

5.a. Vérifier que, pour tout entier naturel non nul $n$, $v_{n+1}=v_{n}\times\dfrac{(n+1)(n+3)}{(n+2)^{2}}$

b. Montrer par récurrence que, pour tout entier naturel non nul $n$, $v_{n}=\dfrac{n+2}{2(n+1)}$

c. Déterminer la limite de la suite $\left(v_{n}\right)$

6. On considère la suite $w_{n}$ dé finie par$w_{1}=\ln\left(u_{1}\right)$, $w_{2}=\ln\left(u_{1}\right)+\ln\left(u_{2}\right)$ et, pour tout entier naturel $n\geq 3$, par
$$w_{n}=\sum_{\lim_{k=1}^{n}}\ln\left(u_{1}\right)+\ln\left(u_{2}\right)+\ldots+\ln\left(u_{n}\right)$$

Montrer que $w_{7}=2w_{1}$

Pour les candidats ayant suivi l'enseignement de spécialité

Pour tout entier naturel $n$, on définit les entiers $a_{n}=6\times 5^{n}-2$ et $b_{n}=3\times 5^{n}+1$

1.a. Montrer que, pour tout entier naturel $n$,chacun des entiers an et $b_{n}$ est congru à $0$ modulo $4$

b. Pour tout entier naturel $n$, calculer $2b_{n}-a_{n}$

c. Déterminer le $PGCD$ de $a_{a}$ et $b_{n}$

 
a. Montrer que $b_{2020}\équiv 3\times 2^{2020}+1[7]$

b. En remarquant que $2020=3\times 673+1$, montrer que $b_{2020}$ est divisible par $7$

c. L'entier $a_{2020}$ est-il divisible par $7$?

Justifier la réponse.

On considère les suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ définies par :

$u_{0}=v_{0}=1$ et,pour tout entier naturel $n$, $\left\lbrace\begin{array}{rcl} u_{n+1}&=&3u_{n}+4v_{n}\\ v_{n+1}&=&u_{n}+3v_{n} \end{array}\right.$

Pour un entier naturel $N$ donné, on souhaite calculer les termes de rang $N$ des suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ et on se demande si l'algorithme ci-dessous permet ce calcul.

$\begin{array}{|c|c|} \hline \text{algortihme}\\ \hline 1&U\longleftarrow 1\\ \hline 2.&V\longleftarrow 1\\ \hline 3.&K\longleftarrow 0\\ \hline 4.&\text{Tant que }K<N\\ \hline 5.&U\longleftarrow 3U+4U\\ \hline 6.&V\longleftarrow U+3V\\ \hline 7.&K\longleftarrow K\longleftarrow k+1\\ \hline 8.&\text{ Fin Tant que }\\ \hline \end{array}$

1. On fait fonctionner l'algorithme avec $N=2$

Recopier et compléter le tableau ci-dessous en donnant les valeurs successivement affectées aux variables $U$, $V$ et $K$
$$\begin{array}{|c|c|c|} \hline U&V&K\\ \hline 1&1&0\\ \hline 7&10&1\\ &&\\ \hline \end{array}$$

2. L'algorithme permet-il effectivement de calculer $u_{N}$ et $v_{N}$ pour une valeur de $N$ donnée ?

Dans le cas contraire, écrire sur la copie une version corrigée de cet algorithme afin que les variables $U$ et $V$ contiennent bien les valeurs de $u_{N}$ et $v_{N}$ à la fin de son exécution.

Pour tout entier naturel $n$, on définit la matrice colonne $X_{n}=\begin{pmatrix} u_{n}\\ v_{n} \end{pmatrix}$

1. Donner, sans justification, une matrice carrée $A$ d'ordre $2$ telle que, pour tout entier naturel $n$ : $$X_{n+1}=AX_{n}$$

2. Montrer par récurrence que, pour tout entier naturel $n$, on a : $X_{n}=A^{n}X_{0}$

3. On admet que,pour tout entier naturel $n$,

$A^{n}=\dfrac{1}{2}\begin{pmatrix} 2\times 5^{n}+2\quad 4\times 5^{n}-4\\ 5^{n}-1\quad 2\times 5^{n}+2 \end{pmatrix}$

Montrer que, pour tout entier naturel $n$, $u_{n}=\dfrac{a_{n}}{4}$ et $v_{n}=\dfrac{b_{n}}{4}$ où $a_{n}$ et $b_{n}$ sont les nombres entiers définis dans la partie $A$

4. Justifier que, pour tout entier naturel $n$, $u_{n}$ et $v_{n}$ sont premiers entre eux.