Bac maths, Polynésie sept 2007

 

4 points

 

On considère un cube $ABCDEFGH$ d'arête de longueur $3.$

 

On choisit le repère orthonormal $(D\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ tel que :

 

$$\vec{i}=\dfrac{1}{3}\overrightarrow{DA}\;,\ \vec{j}=\dfrac{1}{3}\overrightarrow{DC}\;,\ \vec{k}=\dfrac{1}{3}\overrightarrow{DH}$$

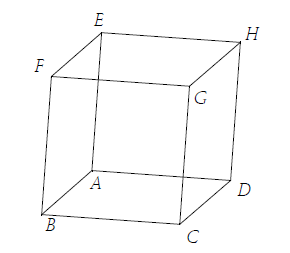
1. a. Donner les coordonnées des points $A\;,\ C\;,\ E.$

 

b. Déterminer les coordonnées du point $L$ barycentre du système ${(C\;,\ 2)\;;\ (E\;,\ 1)}.$

 

c. Déterminer les coordonnées des vecteurs $\overrightarrow{AE}$ et $\overrightarrow{DL}.$

 

2. Soit $(a\;,\ b)$ un couple de réels. On note $M$ le point de la droite $(AE)$ tel que $\overrightarrow{AM}=a\vec{AE}$ et $N$ le point de la droite $(DL)$ tel que $\overrightarrow{DN}=b\vec{DL}.$

 

a. Montrer que le vecteur $\overrightarrow{MN}$ est orthogonal aux vecteurs $\overrightarrow{AE}$ et $\overrightarrow{DL}$ si et seulement si le couple $(a\;,\ b)$ vérifie le système $$\left\lbrace\begin{array}{rcl} -a+2b &=& 1\\ 3a-b &=& 0 \end{array} \right.$$

 

b. En déduire qu'il existe un seul point $M_{0}$ de $(AE)$ et un seul point $N_{0}$ de $(DL)$ tels que la droite $(M_{0}N_{0})$ est orthogonal aux droites $(AE)\ $ et $\ (DL).$

 

c. Déterminer les coordonnées des points $M_{0}$ et $N_{0}$ puis calculer la distance $M_{0}N_{0}.$

1. a. $A(3\;,\ 0\;,\ 0)\;,\ C(0\;,\ 3\;,\ 0)\;,\ E(3\;,\ 0\;,\ 3)$.

 

b. $x_{L}=\dfrac{1}{2+1}(2.x_{C}+1.x_{E})=1\;,\ y_{L}=2\;,\ z_{L}=1$.

 

c. $\overrightarrow{AE}=(0\;;\ 0\;;\ 3)\;,\ \overrightarrow{DL}=(1\;;\ 2\;;\ 1)$.

 

2. Soit $(a\;,\ b)$ un couple de réels. On note $M$ le point de la droite $(AE)$ tel que et $N$ le point de la droite $(DL)$ tel que $\overrightarrow{DN}=b\overrightarrow{DL}.$

 

a.

 

$\begin{array}{rcl} \overrightarrow{AM}&=&a\overrightarrow{AE} \\ \\ &=&(0\;;\ 0\;;\ 3a)\end{array}$

 

$\begin{array}{rcl} \overrightarrow{DN}&=&b\overrightarrow{DL} \\ \\ &=&(b\;;\ 2b\;;\ b) \end{array}$

 

$\begin{array}{rcl} \overrightarrow{MN}&=&\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN} \\ \\ &=&\begin{pmatrix} -3+b\\ 2b\\ -3a+b \end{pmatrix} \end{array}$

 

$\begin{array}{rcl} \overrightarrow{MN}\cdot\overrightarrow{DL}&=&(-3+b).1+2b.2+(-3a+b).1 \\ \\ &=&-3+6b-3a=0 \\ \\ \Leftrightarrow\ 2b-a&=&1\end{array}$

$\begin{array}{rcl} \overrightarrow{MN}\cdot\overrightarrow{AE}&=&(b-3).0+2b.0+(-3a+b).3 \\ \\ &=&3b-9a=0 \\ \\ \Leftrightarrow\ 3a-b&=&0 \end{array}$

 

b. On résout :

 

$\begin{array}{rcl} \left\lbrace\begin{array}{lcl} -a+2b &=& 1\\ 3a-b &=& 0 \end{array} \right.&\Leftrightarrow&\left\lbrace\begin{array}{lcl} 2b-1 &=& a\\ 6b-3-b &=& 0 \end{array} \right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcl} a &=& \dfrac{7}{3}\\ \\ b &=& \dfrac{5}{3} \end{array} \right.\end{array}$ 

 

$(M_{0}N_{0})$ est orthogonale aux droites $(AE)$ et $(DL)$.

 

c. On a donc $\overrightarrow{AM}_{0}=(0\;;\ 0\;;\ 7)\ \Rightarrow\  M_{0}(3\;;\ 0\;;\ 7)$ et 

 

$\overrightarrow{DN}_{0}=\left(\dfrac{5}{3}\;;\ \dfrac{10}{3}\;;\ \dfrac{5}{3}\right)\ \Rightarrow\  N_{0}\left(\dfrac{5}{3}\;;\ \dfrac{10}{3}\;;\ \dfrac{5}{3}\right)$

 

$\begin{array}{rcl} M_{0}N_{0}&=&\sqrt{\left(\dfrac{5}{3}-3\right)^{2}+\left(\dfrac{10}{3}-0\right)^{2}+\left(\dfrac{5}{3}-7\right)^{2}} \\ \\ &=&\sqrt{\dfrac{16}{9}+\dfrac{100}{9}\dfrac{256}{9}} \\ \\ &=&\dfrac{2\sqrt{93}}{3} \end{array}$