Bac Maths ES/L Antilles-Guyane 10 septembre 2019
Exercice 1
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n’est demandée.
Une bonne réponse rap-porte un point.
Une mauvaise réponse, plusieurs réponses ou l’absence de réponse à une question ne rapportent ni n’enlèvent de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante.
1) L'équation $\ln5+l\ln(x+1)=1$ a pour solution :
a) $x=\mathrm{e}-6$
b) $x=-1$
c) $x=\dfrac{1}{5}\mathrm{e}-1$
d) $x=-0.5$
2) Soit $f$ la fonction définie et dérivable sur l’intervalle $]0\ ;\ +\infty[$ par $f(x)=2\ln(x)-x$.
Le nombre $f'(2)$ est égal à :
a) $-1$
b) $0$
c) $2\ln2-2$
d) $2\ln2−1$
3) Le plus petit entier naturel $n$ solution de l'inéquation $2^{n}>175$ est :
a) $n=\ln\left(\dfrac{175}{2}\right)$
b) $n=7$
c) $n=8$
d) $n=\ln175-\ln2$
4) Soit une fonction $f$ définie et dérivable sur l’intervalle $[-3 \ ;\ -1]$.
On note $f'$ sa dérivée et $F$ une de ses primitives.
On sait que pour tout $x$ de l’intervalle $[-3 \ ;\ -1]$, $f'(x)>0$.
On peut affirmer que, sur l’intervalle $[-3 \ ;\ -1]$, la fonction $F$ est :
a) décroissante ;
b) strictement croissante ;
c) convexe ;
d) négative.
Exercice 2 5 points
Il a reçu $1500$ flacons d’un certain modèle provenant de deux sites de production différents, le site $A$ et le site $B.$
Sur les $1500$ flacons de ce modèle reçus, $900$ proviennent du site $A$, les autres du site $B$.
Les trois parties $A$, $B$ et $C$ sont indépendantes.
Si nécessaire,les résultats seront arrondis au millième.
Partie A
Parmi les flacons provenant du site $A$, $95\%$ ont un aspect conforme au cahier des chargestandis que $92\%$ des flacons provenant du site $B$ ont un aspect conforme.
Il prélève auhasardun des flacons qu’il areçuslorsde ladernièrelivraison.
On note :
$A$ l'évènement « Le flacon provient du site $A$ » ;
$B$ l'évènement « Le flacon ne provient du site B » ;
$C$ l'évènement « Le flacon a un aspect conforme au cahier descharges ».
1) Déterminer la probabilité que le flacon provienne du site $A$ etait un aspect conforme au cahier des charges.
2) Montrer que la probabilité que le flacon ait un aspect conforme au cahier des charges est $0.938.$
3) Le flacon prélevé se trouve avoir un aspect non conforme.
Déterminer la probabilité qu’il provienne du site $B$.
Partie B
On admet que le volume de parfum, exprimé en millilitre, contenu dans un flacon prélevé au hasard peut être modélisé par une variable aléatoire $X$ qui suit une loi normale d’espérance $= 100$ et d’écart type $σ = 1$. Déterminer la probabilité qu’un flacon prélevé au hasard soit correctement rempli.
Partie C
Exercice 2
Les poids des arêtes sont les durées moyennes de parcours, en minute, du chasse-neige entre deux stations.
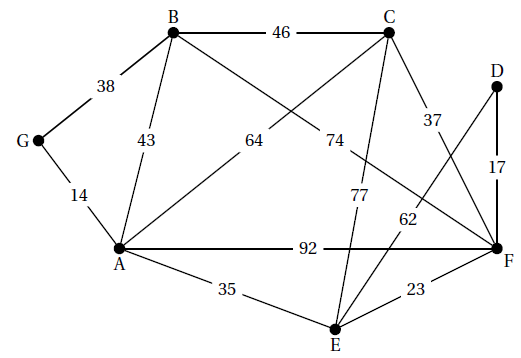
1) Le chasse-neige part de la station $G$.
Peut-il partir de cette station et y revenir en parcourant une et une seule fois chacune des routes, matérialisées parles arêtes decegraphe ?
2) Une saleuse doit de même parcourir l’ensemble des routes du secteur après déblaiement de la neige.
Elle est garée à la station $A$ et, après son travail, peut se garer dans n’importe quelle station.
Peut-elle parcourir une et une seule fois chacune des routes pour traiter l’ensemble du secteur ?
3) On appelle $M$ la matrice d’adjacence associée au graphe, les sommets étant rangés dans l'ordre alphabétique et on donne :
$$M^{4}=\begin{pmatrix}61&48&52&28&45&55&24\\48&44&41&21&42&45&20\\52&41&50&25&41&52&25\\28&21&25&15&20&24&10\\45&42&41&20&44&48&21\\55&45&52&24&48&61&28\\24&20&25&10&21&28&15\\ \end{pmatrix}$$
Interpréter dans le contexte de l’exercice le nombre $10$ figurant en caractère gras dans la matrice.
4) Déterminer, pour le chasse-neige, le chemin le plus rapide pour aller de la station $G$ à la station $D.$
On donnera le par cours trouvé ainsi que sa durée totale.
5) Le conducteur du chasse-neige part de la station $G$ et va directement à la station $A.$
Il apprend alors que la route allant de la station $E$ à la station $F$ est barrée.
Comment peut-il terminer son parcours au plus vite jusqu’à la station $D$ ?
Préciser le temps qu’il mettrait alors pour finir son parcours. Aucune justification n’est attendue ici.
Exercice 3
On modélise l’évolution du nombre d’arbres de cette parcelle par une suite $(u_{n})$ dans laquelle,
Pour tout entier naturel $n\;,\ u_{n}$ est le nombred’arbres de la parcelle en $2018+n$ , ainsi $u_{0} =10000$.
Partie A
2. On définit la suite $(v_{n})$ par $v_{n} =u_{n} −3000$ pourtout entier naturel $n.$
a. Montrer que la suite $(v_{n})$ est une suite géométrique dont on précisera la raison et le premier terme $v_{0}.$
b. Pourtout entier naturel $n$, exprimer $v_{n}$ en fonction de $n.$
c. En déduire que pour tout entier naturel $n\;,\ u_{n}=7000\times 0.8^{n}+3000.$
d. Si le réaménagement de cette parcelle se poursuit selon ce même modèle, que peut-on conjecturer à long terme concernant le nombre d’arbres de celle-ci ?
Partie B
1. On admet que la suite $(u_{n})$ est décroissante.
Dans les algorithmes ci-dessous, $U$ est un nombre réel et $N$ est un nombre entier.
Parmi ces algorithmes ci-dessous, un seul donne le nombre d’années nécessaires pour que le nombre d’arbres devienne inférieur ou égal à $4000$.
$$\boxed{U\leftarrow 10000\\N\leftarrow 0\\\text{Tant que }U>4000\\\quad N\leftarrow N+1\\\quad U\leftarrow 0.8^{N}\times U+600\\\text{Fin Tant Que}}$$
$$\boxed{U\leftarrow 10000\\N\leftarrow 0\\\text{Tant que }U>4000\\\quad N\leftarrow N+1\\\quad U\leftarrow 0.8\times U+600\\\text{Fin Tant Que}}$$
Exercice 4
La droite $\mathcal{D}$ est la tangente à la courbe $\mathcal{C}$ au point d’abscisse $0$ ; elle passe par le point $A$ de coordonnées $(0.5\ ;\ 1).$
La tangente $T$ à la courbe $\mathcal{C}$ au point d’abscisse $1$ est parallèle àl’axe des abscisses.
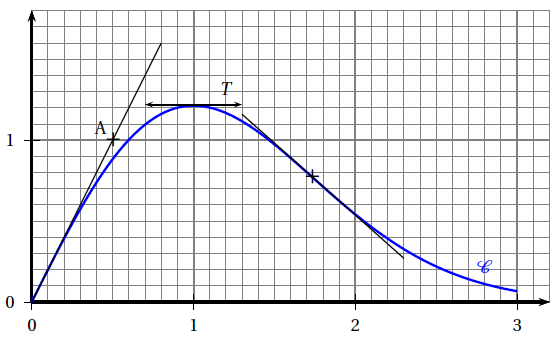
Partie A
2. Donner la valeur de $f '(1).$
3. Proposer un intervalle sur lequel la fonction semble concave.
Partie B
$$f (x) = 2xe^{−0.5x^{2}}.$$
1. On note $f '$ la fonction dérivée de $f$ sur l’intervalle $[0\ ;\ 3].$
a. Montrer que $f '(x) =(2−2x^{2})e^{−0.5x^{2}}.$
b. Étudier les variations de la fonction $f$ sur l’intervalle $[0\ ;\ 3]$ et dresser son tableau de variation.
2. On admet que la fonction F, définie par $F(x) = -2e^{−0.5x^{2}}$, est une primitive de $f$ sur l’intervalle $[0\ ;\ 3].$
En déduire la valeur moyenne de $f$ sur l’intervalle $[0\ ;\ 3]$ et en donner une valeur approchée au millième.
Partie C
Un journal affirme que cet hiver :
$-\ $ le nombre de lits occupés lors du pic de la maladie a dépassé le million ;
$-\ $ le nombre moyen de lits occupés sur les trois mois a été d’environ $40\ 0000.$
Que dire de ces deux affirmations ?

Ajouter un commentaire