BAC BLANC 2024

Exercice 1 :

Pour chaque question, une et une seule des quatre propositions est exacte.

Donner la bonne réponse. Barème par réponse : réponse correcte$ 0,5$ point, absence de réponse $0$ point
Le plan est muni d’un repère orthonormé$(O; \vec{i},\vec{j})$. $A, B$ et $C$ sont trois points d’affixes respectives :

$z_{A} = −2 + i ; z_{B} =\dfrac{1}{2}+\dfrac{1}{2}i$ et $z_{c} = −1 + i\sqrt{3}$ ..

1 °) La forme exponentielle de $z_{c} = −1 + i\sqrt{3}$ est :
a) $2e^{i\dfrac{2π}{3}}$ ; b) $−e^{i\sqrt{3}}$; c)$−2e^{−i\dfrac{2π}{3}}$ ; d)$ \sqrt{2}e^{i\dfrac{7π}{3}}$

2°) $arg(\dfrac{z_{B}−z_{A}}{z_{C}−z_{A}})$ est une mesure de l’angle :

a)$ (\vec{AC}, \vec{BC}) $; b) $(\vec{CA}, \vec{BC})$ ; c) $(\vec{AC}, \vec{BA})$ ; d)$ (\vec{BA}, \vec{AC})$
3°) L’ensemble des points $M(z)$ du plan tel que $|z + 2 − i| = |z −\dfrac{1+i}{2}|$ est :

a) Le cercle de centre $B$ et de rayon $1$ ; b) La médiatrice du segment $[BA]$

c) la droite $(BA)$ ; d) La droite $(AB)$ privée du point$ B$

4°) Une primitive de la fonction $\dfrac{lnx}{x}$ dans l’intervalle $]0; +∞[$ est :

a)$\dfrac{1}{2}ln2x $; b) $\dfrac{1−lnx}{x^{2}}$; c) $ln|lnx| $; d)$ln2x$

5°) $∀ a ∈ R ∖ {0} ln(a^{2})$ est égale à :

a) $2lna$ ; b)$(lna)(lna) $; c)$ 2ln|a| $; d) $(lna)^{2}$

EXERCICE 2 :

Le plan complexe est rapporté à un repère orthonormé direct$(O; \vec{i},\vec{j})$.

On considère les applications : $f: z′ =\dfrac{1 + i\sqrt{3}}{2}z +\dfrac{\sqrt{3} + i}{2}$ et $g: z′ = −2z + 3i$ .

On pose : $h = f ∘ g$ et le point $Ω(i)$

1) Déterminer la nature de chacune des deux applications $f$ et $g$ et leurs éléments caractéristiques.

2) On considère le point $A(a)$ avec $a$ un nombre complexe donné différent de $i$. On pose :
$B = h(A) , C = h(B)$ et $D = h(C)$ .

a) Montrer que si le point $M′(z ′)$ est l’image du point $M(z)$ par l’application $h$ alors :

$z ′ − i = 2e^{i\dfrac{4π}{3}} (z − i)$ .

b) Déterminer la nature de h et ses éléments géométriques caractéristiques.

3) a) Déterminer en fonction du nombre complexe a, les complexes $b, c$ et $d$, affixes respectives de $B , C$ et $D$.

b) Montrer que les points $Ω , A$ et $D$ sont alignés.

c) Démontrer que $Ω$ est le barycentre du système pondéré ${(B, 4); (C, 2); (D,
1)}$.

EXERCICE 3

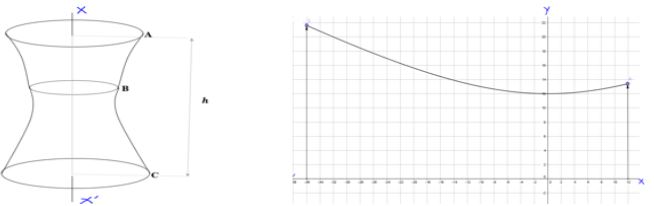
Une tour de condenseur a une hauteur $h = 48m$, sa base est circulaire et a un rayon $R$.

Son orifice supérieur a un rayon $R′$

Son volume peut etre considéré comme le volume du solide de révolution engendré par la rotation de la courbe de la fonction $f$ , définie par $f(x) = 12 × \sqrt{1 +\dfrac{x^{2}}{576}}$ définie sur$ ⌈−36; 12⌉ $, autour de l’axe des abscisses dans le repère orthonormé $(O; \vec{i},\vec{j})$, unite; $2cm$

Calculons le volume de la tour

Problème :

Soit $f$ la fonction numérique définie par :$$\left\lbrace\begin{array}{rcl}    
f(x) &=&\dfrac{x^{2}}{x−1}e^{\dfrac{1}{x}} + 1 si x < 0\\
f(x)& =& e^{x} + x(−1 + ln x) si x > 0\\
    f(0)& =& 1
\end{array}\right.$$

On note $(C_{f})$ sa courbe dans le plan muni d’un repère orthonormal $(O; \vec{i},\vec{j})$(unité : 1 cm).
    

Partie A :

Soit $g$ la fonction définie sur $=]0; +∞[=$ par : $=g(x) = e^{x} + ln x=$.
    

1) Préciser le sens de variation de $g$.

2) Montrer que l’équation g(x) = 0 admet dans $]0; +∞[$ une unique solution $α$.

Vérifier que $0,2 < α < 0,3$.

3) Préciser le signe de $g(x)$ suivant les valeurs de $x$.
    

Partie B :

    
1) Montrer que $f$ est définie sur $R$.

2) a) Etudier les limite de $f$ en $−∞$ et en $+∞$.

b) Montrer que la droite d’équation $y = x + 3$ est une asymptote oblique de $(C_{f})$ en$ −∞$.

c) Etudier la nature de la branche infinie de $(C_{f})$ en $+∞$.

3) a) Montrer que $f$ est continue en$ 0$.

b) Etudier la dérivabilité de $f$ en $0$.

Interpréter graphiquement les résultats obtenus.

4) a) Montrer que $f$ est dérivable sur $]−∞; 0[$ et que pour tout $x ∈ ]−∞; 0[, f′(x) =\dfrac{(x^{2}−3x+1)e^{\dfrac{1}{x}}}{(x−1)^{2}}$

En déduire le signe de $f′(x)$ sur $]−∞; 0[$.

b) On admet que $f$ est dérivable sur $]0; +∞[$ puis calculer $f′(x)$.

c) Dresser le tableau de variations de $f$.

5) Tracer la courbe $(C_{f})$ dans le repère $(O; \vec{i},\vec{j})$.

6) a) A l′aide d′une intégration par parties, calculer l′intégrale $I =\int_{2}^{1}x ln x dx$    .

b) En déduire l′aire, en $cm2$, du domaine limité par $(C_{f})$, l_′axe des abscisses et les droites d′équations $x = 1$ et $x = 2$.

7) Soit $h$ la restriction de $f$ à l’intervalle $]−∞; 0]$.

a) Montrer que $h$ admet une fonction réciproque $h^{−1}$ dont on précisera l’intervalle de définition.
    
b) Tracer la courbe $(C_{h^{−1}})$ dans le repère précédent.