Corrigé BFEM Maths 2020
Exercice 1
1) La modalité qui a le grand effectif est appelée :
b) le mode
2) −(−2)+3(0)−5<0⇒−3<0 vrai donc E(−2 ; 0) appartient au demi-plan solution de l'inéquation −x+3y−5<0
3) On considère l'application affine g définie par g(x)=(2−√3)x−7
a) le coefficient de cette application est (2−√3) et l'ordonnée à l'origine −7
b) g(4√3−5)=(2−√3)(4√3−5)−7=−29+13√3
4)A2=(√3−12)2=3−2√3+14=4−2√34⇒A2=2−√32
B=√1−√32=√2−√32=√(√3−12)2=|√3−12|
Cherchons le signe de √3−12
(√3)2=312=1}
(√3)2>12 donc √3−1>0
d'où √3−12>0 donc B=|√3−12|=√3−12
Exercice 2
1) Sachant que l'âge moyen est de 26 ans, montre que m et n vérifient le système :
{m+n=819m+27n=176
Classes[17 ; 21[[21 ; 25[[25 ; 29[[29 ; 33[Effectifsm=56n=310Centre de classes19232731ECC5111424FCC(%)20.845.858.3100
− m+6+n+10=24⇒m+n=24−16=8
− moy=19m+23×6+27n+31×1024=26⇒19m+138+27n+31024=26⇒19m+27n+448=624
D'où 19m+27n=624−448=176 donc m et n vérifient le système
{m+n=819m+27n=176
Après résolution on trouve m=5 et n=3
2) Pour la suite de l'exercice, on donne : m=5 et n=3.
a) voir tableau.
b) le nombre de mères ayant moins de 29 ans à la naissance de leur premier enfant :
c) la fréquence des mères ayant au moins 25 ans à la naissance de leur premier enfant est :
f=3+1024
3) a) voir figure
b) âge médian en utilisant le théorème de Thalès :
me−254=12−113⇒me=26.3
Exercice 3
Une pyramide régulière SABCD à base carrée de hauteur SO=√34m représente la charpente du toit d'un hangar. La longueur de l'arête SA=√34m
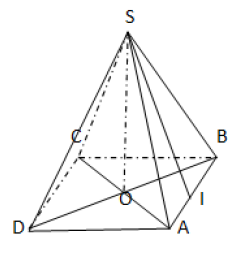
1)OA2=SA2−SO2⇒OA2=34−16=18donc OA=√18=3√2
AB2=2OA2⇒AB2=2×18=36donc AB=√36=36
2) Le volume de cette pyramide
V=AB2×SO3=36×43=48m3
3) Aire latérale
AL=Périmètre de base×apothème2
Calcul de l'apothème SI
SIA rectangle en I
donc SI2=SA2−IA2=34−9=25⇒SI=√25=5
AL=4×6×52
le prix d'achat des tôles nécessaires à la construction de la toiture
Prix=60×3000 F=180 000 F.
Exercice 4
1) Choisis la bonne réponse
a) Si F est le symétrique de E par rapport à A alors : →AF=→EA
b) Si E est le milieu de [AB] alors : →AE=−12→BA
2) On donne les vecteurs →u((ef)) et →v((ab)).
→u et →v sont colinéaires équivaut à : eb−af=0.
3) Dans un repère orthonormal (O, →I ; →J) place les points A(−1 ; 1) ; B(3 ; −1) et C(5 ; 3)
a) Coordonnées des vecteurs →AB ; →AC et →BC
→AB(4−2) ; →AC(62) et →BC((24)
b) Montrons que le triangle est rectangle.
Vérifions que les vecteurs →AB((4−2) et →BC(24) sont orthogonaux.
4×2+(−2)×4=8−8=0
donc →AB((4−2) et →BC((24) sont orthogonaux d'où ABC rectangle en B
c) Calcule les coordonnées du point D image de A dans la translation de vecteur →BC
Soit D(x ; y). D image de A dans la translation de vecteur →BC donc →AD=→BC
→AD(x+1y−1)=→BC(24)
⇒{x+1=2y−1=4
⇒{x=1y=5
donc D(1 ; 5)
d) Soit (C) le cercle circonscrit au triangle ABC.
E est milieu de [AC] d'où E(−1+52 ; 1+32) E(2 ; 2)
Équation de la droite (L) tangente au cercle en B.
Soit M(x ; y) un point de (L)
→BM et →BE sont orthogonaux
→BM(x−3y+1) et →BE(−13) sont orthogonaux donc −1(x−3)+3(y+1)=0
−x+3+3y+3=0⇒(L)=−x+3y+6=0

Ajouter un commentaire