Corrigé Bac Physique Chimie 1er groupe S1-S3 2014
Exercice 1
1.1.1
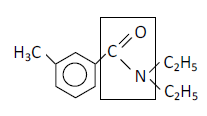
Groupe fonctionnel amide
1.1.2
a) formule de l'amine : $C_{2}H_{5}-NH-C_{2}H_{5}$
nom : diéthylamine
classe : amine secondaire
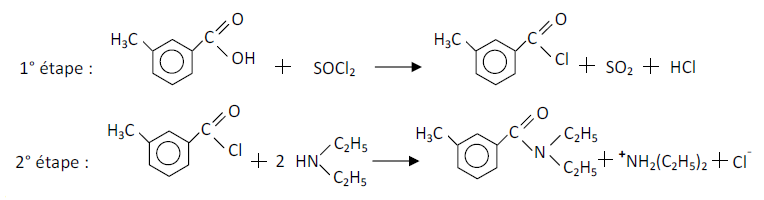
b) Équations-bilans de la préparation :
1.1.3
Nom officiel : N, N-diéthyl-3méthylbenzamide
1.2
Formule de l'IR3535
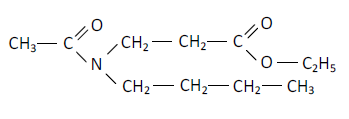
Exercice 2
2.1 Équation-bilan de la réaction et nom des produits :

2.2
2.2.1 La vitesse de formation $v$ est définie par : $V=+\dfrac{dn}{dt}$ ; sa valeur correspond au coefficient directeur de la tangente à la courbe $n=f(t)$ à la date $t$ considérée.
A chaque date, on trace la tangente à la courbe $n=f(t)$ ; et on détermine le coefficient directeur.
On obtient les résultats suivants :
A $t=2\;min\ :\ v_{2}=43\;mmol.min^{-1}$
A $t=5\;min\ :\ v_{5}=17\;mmol.min^{-1}$
On a : $v_{5}<v_{2}$ , donc la vitesse diminue.
Justification : la concentration des réactifs diminue entraînant ainsi la diminution de la vitesse.
2.2.2 Définition du temps de demi-réaction $t_{1/2}$
Le temps de demi-réaction est le temps au bout duquel la moitié de la quantité de matière initiale du réactif limitant a réagi.
2.2.3
a) D'après le graphe la quantité de matière d'éthanoate de sodium obtenue est : $n_{f}=200\;\mu moL$
b) A la date $t_{1/2}$ on a : $n_{\text{ester formé}}=\dfrac{n_{\text{ester finale}}}{2}=100\;\mu mol$ d'où, d'après le graphe, $t_{1/2}=1.6\;min.$
2.3.
2.3.1
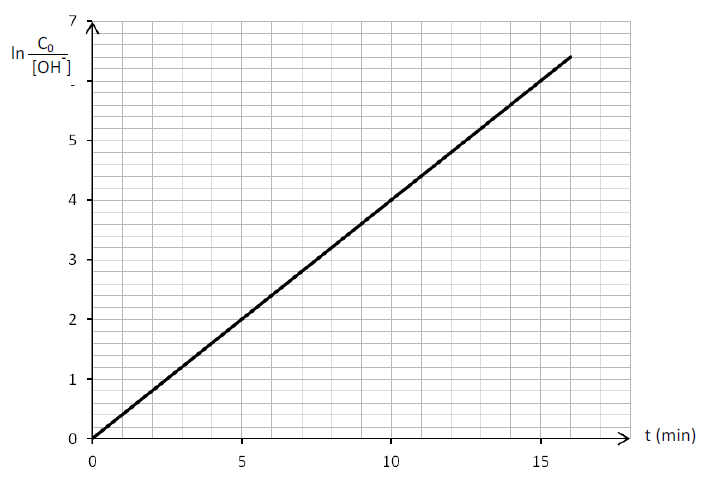
a) Tracé de la courbe $\ln\left(\dfrac{C_{0}}{[OH^{-}]}\right)=f(t)$ :
b) Relation :
On a une droite qui passe par l'origine donc, $$\ln\dfrac{C_{0}}{[OH^{-}]}=kt\quad(1)\quad\text{avec } k=\text{pente}=0.4\;min^{-1}$$
2.3.2
A la date $t_{1/2}$ la moitié des ions $OH^{-}$ a réagi donc, $$[OH^{-}]_{1/2}=\dfrac{C_{0}}{2}\quad(2)$$
2.3.3
Les équations (1) et (2) entraînent, à $t_{1/2}$ :
$\begin{array}{rcrcl}\ln\dfrac{C_{0}}{[OH^{-}]_{1/2}}=kt_{1/2}&\Rightarrow& \ln\dfrac{C_{0}}{\dfrac{C_{0}}{2}}&=&kt_{1/2}\\ \\&\Rightarrow&t_{1/2}&=&\dfrac{\ln 2}{k}\end{array}$
Valeur de la constante $k\ :\ k=0.4\;min^{-1}$
2.3.4 : Valeur de $t_{1/2}$ :
On a : $t_{1/2}=\dfrac{\ln 2}{0.4}=1.7\;min$
Il y a accord entre les 2 valeurs; l'erreur relative est : $\dfrac{\Delta t_{1/2}}{t_{1/2}}=0.06\ $ soit $\ 6\%$
Exercice 3
3.1 Expression de $U_{0}$ :
Théorème de l'énergie cinétique : $qU_{0}=\dfrac{1}{2}mv_{0}^{2}$
D'où, $U_{0}=\dfrac{mv_{0}^{2}}{2q}$
3.2
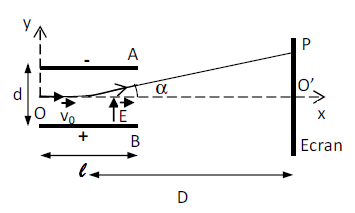
3.2.1 Représentation du champ $\vec{E}$
$U_{AB}<0\ \Rightarrow\ v_{A}<v_{B}\ $ or $\ \vec{E}$ est dirigé vers les potentiels décroissants.
Ainsi, $\vec{E}$ a le sens de $B$ vers $A$
3.2.2 Équation de la trajectoire :
Système : particule
Référentiel terrestre (galiléen)
Bilan des forces : force électrostatique $\vec{F}=q\vec{E}$
Théorème du centre d'inertie :
$\begin{array}{rcl} q\vec{E}=m\vec{a}&\Rightarrow&\vec{a}=\dfrac{q\vec{E}}{m}\\ \\&\Rightarrow&\vec{a}\;\left\lbrace\begin{array}{rcl} a_{x}&=&0\\ \\a_{y}&=&\dfrac{qE}{m}\end{array}\right.\\ \\&\Rightarrow&\vec{v}\;\left\lbrace\begin{array}{rcl} v_{x}&=&v_{0}\\ \\v_{y}&=&\dfrac{qE}{m}t\end{array}\right.\\ \\&\Rightarrow&\overrightarrow{OM}\;\left\lbrace\begin{array}{rcl} x&=&v_{0}t\\ \\ y&=&\dfrac{qE}{m}t^{2}\end{array}\right.\end{array}$
On a : $t=\dfrac{x}{v_{0}}$ ; on remplace dans $y\ \Rightarrow\ y=\dfrac{qE}{2mv_{0}^{2}}x^{2}$ ; la trajectoire est parabolique.
3.2.3 Ordonnée $y_{S}$ du point de sortie :
$x_{S}=\ell$ soit $y_{S}=\dfrac{qE}{2mv_{0}^{2}}\ell^{2}$ avec $E=\dfrac{U}{d}$ soit $y_{S}=\dfrac{qU}{2mdv_{0}^{2}}\ell^{2}$
3.2.4 Condition de sortie :
$\begin{array}{rcrcl} y_{S}<\dfrac{d}{2}&\Rightarrow&\dfrac{qU}{2mdv_{0}^{2}}\ell^{2}&<&\dfrac{d}{2}\\ \\&\Rightarrow&U&<&\dfrac{mdv_{0}^{2}}{q\ell^{2}}\end{array}$
3.3
3.3.1 Nature du mouvement de la particule à la sortie du champ électrique :
A la sortie du champ électrique, la particule n'est soumise à aucune force, donc son mouvement est rectiligne et uniforme.
3.3.2 Déviation de la particule $Y=O'P$
$\begin{array}{rcrcl}\tan\alpha=\dfrac{Y}{D}=\dfrac{y_{S}}{\dfrac{\ell}{2}}&\Rightarrow&Y&=&\dfrac{2Dy_{S}}{\ell}\\ \\&\Rightarrow&Y&=&\dfrac{DqU\ell}{mdv_{0}^{2}}\end{array}$
3.4
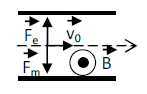
3.4.1 Représentation de $\vec{B}$
La particule est soumise à la force électrique $\vec{F}_{e}$ et à la force magnétique $\vec{F}_{m}$
On a : $\vec{F}_{e}+\vec{F}_{m}=\vec{0}$ ; donc $\vec{F}_{m}$ est opposée à $\vec{F}_{e}$
Or le trièdre $(q\vec{v}_{0}\;,\ \vec{B}\;,\ \vec{F}_{m})$ est direct donc, $\vec{B}$ sortant.
3.4.2 Intensité $B$ du champ magnétique :
$\begin{array}{rcrcl}\vec{F}_{e}+\vec{f}_{m}=\vec{0}&\Rightarrow&F_{e}&=&F_{m}\\ \\&\Rightarrow&qE&=&qv_{0}B\\ \\&\Rightarrow&B&=&\dfrac{E}{v_{0}}\\ \\&&&=&\dfrac{U}{dv_{0}}\end{array}$
A.N : $B=\dfrac{400}{2\;10^{-2}\times 1.6\;10^{6}}=1.25\;10^{-2}\;T$
3.4.3 Charge massique $\dfrac{q}{m}$ en fonction de $Y\;,\ \ell\;,\ D\;,\ d\;,\ U\ $ et $\ B.$
$Y=\dfrac{DqU\ell}{mdv_{0}^{2}}\ \Rightarrow\ \dfrac{q}{m}=\dfrac{Ydv_{0}^{2}}{DU\ell}\ $ et $\ v_{0}^{2}=\dfrac{U^{2}}{d^{2}B^{2}}$
Soit $\dfrac{q}{m}=\dfrac{YdU^{2}}{DU\ell d^{2}B^{2}}=\dfrac{YU}{D\ell dB^{2}}$
3.4.4 Calcul de la charge massique :
$\dfrac{q}{m}=\dfrac{1.5\;10^{-2}\times 400}{40\;10^{-2}\times 5\;10^{-2}\times 2\;10^{-2}\times(1.25\;10^{-2})^{2}}=9.6\;10^{7}\;C.kg^{-1}$ ; La particule est un proton.
Exercice 4
4.1 : Schéma du dispositif
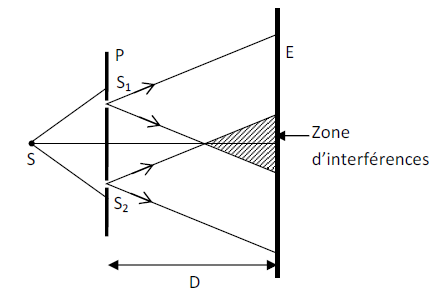
4.2 Vibrations de $S_{1}\ $ et $\ S_{2}\ :\ Y_{01}=Y_{02}=S_{0}\sin\omega t$
4.2.1 Expression des vibrations au point $M$ de l'écran.
Les vibrations en $M$ accusent par rapport aux vibrations de $S_{1}\ $ et $\ S_{2}$ un retard respectif de : $$\left\lbrace\begin{array}{rcl} t_{1}&=&\dfrac{d_{1}}{c}\\ \\ t_{2}&=&\dfrac{d_{2}}{c}\end{array}\right.$$
Vibration issue de $S_{1}\ :\ Y_{1}(M)=S_{0}\sin\omega\left(t-\dfrac{d_{1}}{c}\right)$
Vibration issue de $S_{2}\ :\ Y_{2}(M)=S_{0}\sin\omega\left(t-\dfrac{d_{2}}{c}\right)$
4.2.2 Le coefficient $2S_{0}\cos\left(\dfrac{\pi\delta}{\lambda}\right)$ est l'amplitude de la vibration $Y$ ; cela correspond à la valeur maximale de $Y$ au point considéré.
4.2.3
a) L'intensité lumineuse $E$ s'écrit :
$E=CA^{2}=C\times 4S_{0}\cos^{2}\left(\dfrac{\pi\delta}{\lambda}\right)\quad\text{or }\cos^{2}x=\dfrac{1+\cos 2x}{2}$
$\begin{array}{rrcl}\Rightarrow&\cos^{2}\left(\dfrac{\pi\delta}{\lambda}\right)&=&\dfrac{1+\cos\left(\dfrac{2\pi\delta}{\lambda}\right)}{2}\\ \\\Rightarrow&2\cos^{2}\left(\dfrac{\pi\delta}{\lambda}\right)&=&1+\cos\dfrac{2\pi}{\lambda}\dfrac{ax}{D}\\ \\ & &=&1+\cos\dfrac{2\pi x}{i}\quad\text{or }i=\dfrac{\lambda D}{a}\end{array}$
d'où,
$\begin{array}{rrcl}&E&=&2S_{0}^{2}C\left(1+\cos\dfrac{2\pi}{i}\right)\\ \\\Rightarrow&E&=&E_{0}\left(1+\cos\dfrac{2\pi}{i}\right)\quad\text{avec }E_{0}=2S_{0}^{2}C\end{array}$
b) Les valeurs de $E$ et la courbe $E(x)=f(x)$ :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|}\hline x&-i&-3i/4&-i/2&-i/4&0&i/4&i/2&3i/4&i\\ \hline E(x)&2E_{0}&E_{0}&0&E_{0}&2E_{0}&E_{0}&0&E_{0}&2E_{0}\\ \hline\end{array}$$
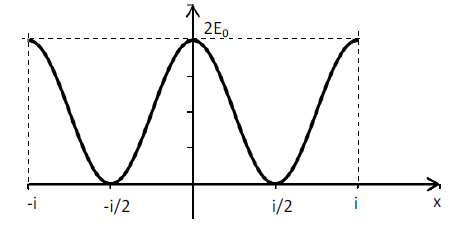
c) Du graphe on déduit :
$\centerdot\ \ $ abscisses des points où l'éclairement est maximal dans l'intervalle considéré : $$x=\left\{-i\;;\ 0\;;\ i\;;\ \ldots\right\}$$
$\centerdot\ \ $ abscisses des points où l'éclairement est nul dans l'intervalle considéré : $$x=\left\{-\dfrac{i}{2}\;;\ \dfrac{i}{2}\;;\ \ldots\right\}$$
$\centerdot\ \ $ distance séparant deux franges consécutives de même nature $$d=x_{n+1}-x_{n}=i$$
4.3
4.3.1
$\begin{array}{rcrcl} d=10i_{1}&\Rightarrow&d&=&10\lambda_{1}\dfrac{D}{a}\\ \\&\Rightarrow&\lambda_{1}&=&\dfrac{ad}{10D}\end{array}$
A.N : $\lambda_{1}=4.8\;10^{-7}\;m=480\;nm$
On mesure la distance correspondant à 10 interfranges au lieu de celle qui correspond à 1 interfrange pour avoir une détermination plus précise de l'interfrange. L'erreur de mesure est amoindrie.
4.3.2
Pour la lumière de longueur d'onde $\lambda_{1}$, au point considéré on a : $$x_{a}=k\lambda_{1}\quad\text{avec } k=2$$
Pour la lumière de longueur d'onde $\lambda_{2}$, au point considéré on a : $$x_{b}=(2k'+1)\dfrac{\lambda_{2}}{2}\quad\text{avec } k'=1$$
$\begin{array}{rcrcl} x_{a}=x_{b}&\Rightarrow&\dfrac{3}{2}\lambda_{2}&=&\lambda_{1}\\ \\&\Rightarrow&\lambda_{2}&=&640\;nm\end{array}$
Exercice 5
5.1 Schéma + branchements de l'oscilloscope :
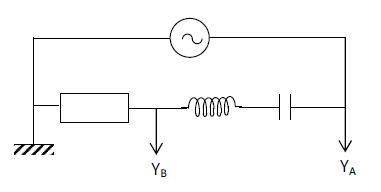
5.2 La base des temps est restée la même sur les figures $5a$ et $5b.$ Par contre la sensibilité verticale a changé ; elle a augmenté.
5.3
5.3.1 : 1 correspond à $u(t)$ et 2 à $u_{R(t)}$ parce que la tension maximale aux bornes du GBF est supérieure à celle aux bornes du résistor (dans l'état actuel de fonctionnement du circuit).
5.3.2 Loi d'Ohm : $u_{R}=Ri\ \Rightarrow\ i=\dfrac{U_{R}}{R}$ donc, $i\ $ et $\ u_{R}$ sont proportionnelles ; ainsi, en visualisant $u_{R}$, on visualise en même temps $i.$
5.4
5.4.1 La fréquence des oscillations :
La période $T$ correspond à 10 divisions ; d'où : $$N=\dfrac{1}{T}=\dfrac{1}{10\;10^{-3}}=100\;Hz$$
5.4.2 Valeur maximale de la tension $u(t)$ : $$U_{\text{max}}=S_{v}.Y_{A}=0.2\times 4=0.8\;V$$
Valeur maximale de l'intensité $i(t)$ :
$\begin{array}{rcrcl} U_{R\text{max}}=S_{v}.Y_{B}=0.2\times 2.5=0.5\;V&\Rightarrow&I_{\text{max}}&=&\dfrac{U_{R\text{max}}}{R}\\ \\& & &=&\dfrac{0.5}{50}\\ \\& & &=&10^{-2}\;A\end{array}$
Valeur de l'impédance : $$Z=\dfrac{U_{\text{max}}}{I_{\text{max}}}=80\;\Omega$$
5.4.3 Le déphasage entre $u\ $ et $\ i$
On a :
$\begin{array}{rcrcl}\dfrac{|\varphi|}{2\pi}=\dfrac{\theta}{T}&\Rightarrow&|\varphi|&=&\dfrac{2\pi\theta}{T}\\ \\& & &=&\dfrac{2\pi\times 1}{10}\\ \\& & &=&\dfrac{\pi}{5}\end{array}$
La tension $u$ est en avance sur $u_{R}$ puisqu'elle atteint en premier son maximum ; $\varphi=+\dfrac{\pi}{5}$
Valeur de $r$
On a : $\cos\varphi=\dfrac{R+r}{Z}\ \Rightarrow\ r=Z\cos\varphi-R$
A.N : $r=80\cos\dfrac{\pi}{5}-50=14.7\;\Omega$
Valeur de $L$
$\begin{array}{rcrcl}\sin\varphi=\dfrac{L\omega-\dfrac{1}{C\omega}}{Z}&\Rightarrow&L\omega&=&Z\sin\varphi+\dfrac{1}{C\omega}\\ \\&\Rightarrow&L&=&\dfrac{Z\sin\varphi}{\omega}+\dfrac{1}{C\omega^{2}}\end{array}$
A.N : $L=0.4\;H$

Ajouter un commentaire