Corrigé Bac Maths S2,S2A,S4,S5 1er groupe - 2022
Exercice 1
Le plans complexe est muni d'un repère orthonormé direct $\left(O\;,\ \vec{u}\ ;\ \vec{v}\right).$
Soit le nombre complexe $a$ définit par :
$a=\sqrt{2-\sqrt{3}}-\mathrm{i}\sqrt{2+\sqrt{3}}.$
1) Montrons que $a^{2}=-2\sqrt{3}-2\mathrm{i}.$
\begin{eqnarray} a^{2}&=&\left(\sqrt{2-\sqrt{3}}-\mathrm{i}\sqrt{2+\sqrt{3}}\right)^{2}\nonumber\\\\ &=&2-\sqrt{3}-2-\sqrt{3}-2\mathrm{i}\sqrt{(2-\sqrt{3})(2+\sqrt{3}}\nonumber\\\\ &=&-2\sqrt{3}-2\mathrm{i}\sqrt{1}\end{eqnarray}
D'où $\boxed{a^{2}=-2\sqrt{3}-2\mathrm{i}}$
Déduisons-en le module de $a$
\begin{eqnarray} \left|a^{2}\right| &=&4\nonumber\\\\\Rightarrow\left|a\right| &=&4\nonumber\\\\\Rightarrow\left|a\right| &=&2 \end{eqnarray}
2) Écrivons $a^{2}$ sous forme trigonométrique.
\begin{eqnarray} a^{2}&=&-2\sqrt{3}-2\mathrm{i}\nonumber\\\\ &=&4\left(-\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}\mathrm{i}\right)\nonumber\\\\ &=&4\left[\cos\left(\dfrac{7\pi}{6}\right)+\mathrm{i}\sin\left(\dfrac{7\pi}{6}\right)\right] \end{eqnarray}
D'où $\boxed{a^{2}=4\left(\cos\dfrac{7\pi}{6}+\mathrm{i}\sin\dfrac{7\pi}{6}\right)}$
Vérifions qu'une des meures de l'argument de $a$ est $\dfrac{19\pi}{12}$
\begin{eqnarray} \text{arg}\left(a^{2}\right)&\equiv &\dfrac{7\pi}{6}[2\pi]\nonumber\\\\\Rightarrow 2\text{arg}(a)&\equiv &\dfrac{7\pi}{12}[\pi] \end{eqnarray}
$\text{où arg}(a)=\dfrac{7\pi}{12}+k\pi\;,\ k\in\mathbb{Z}.$
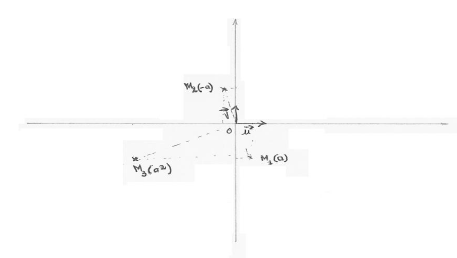
Prenons $k=1\;,\ \boxed{\text{arg}(a)=\dfrac{7\pi}{12}+\pi=\dfrac{19\pi}{12}}$
3) Déduisons-en les valeurs exactes de $\cos\left(\dfrac{7\pi}{12}\right)$ et $\sin\left(\dfrac{7\pi}{12}\right).$
\begin{eqnarray} a&=&2\left[\cos\dfrac{19\pi}{12}+\mathrm{i}\sin\dfrac{19\pi}{12}\right]\nonumber\\\\&=&2\left[\cos\left(\dfrac{7\pi}{12}+\pi\right)+\mathrm{i}\sin\left(\dfrac{7\pi}{12}+\pi\right)\right]\nonumber\\\\&=&-2\cos\dfrac{7\pi}{12}-2\mathrm{i}\sin\dfrac{7\pi}{12} \end{eqnarray}
D'où $\boxed{a=\sqrt{2-\sqrt{3}}-\mathrm{i}\sqrt{2+\sqrt{3}}}$
Ce qui implique que $\cos\left(\dfrac{7\pi}{12}\right)=-\dfrac{\sqrt{2-\sqrt{3}}}{2}$ et $\sin\left(\dfrac{7\pi}{12}\right)=\dfrac{\sqrt{2+\sqrt{3}}}{2}$
Déduisons-en les valeurs exactes de $\cos\left(\dfrac{\pi}{12}\right)$ et $\sin\left(\dfrac{\pi}{12}\right).$
$\dfrac{\pi}{12}=\dfrac{7\pi}{12}-\dfrac{6\pi}{12}=\dfrac{7\pi}{12}-\dfrac{\pi}{2}$
\begin{eqnarray} \cos\left(\dfrac{\pi}{12}\right)&=&\cos\left(\dfrac{7\pi}{12}-\dfrac{\pi}{2}\right)\nonumber\\\\&=&\cos\left(\dfrac{\pi}{2}-\dfrac{7\pi}{12}\right)\nonumber\\\\&=&\sin\left(\dfrac{7\pi}{12}\right)\nonumber\\\\&=&\dfrac{\sqrt{2+\sqrt{3}}}{2} \end{eqnarray}
\begin{eqnarray} \sin\left(\dfrac{\pi}{12}\right)&=&\sin\left(\dfrac{7\pi}{12}-\dfrac{\pi}{2}\right)\nonumber\\\\&=&-\sin\left(\dfrac{\pi}{2}-\dfrac{7\pi}{12}\right)\nonumber\\\\&=&-\cos\left(\dfrac{7\pi}{12}\right)\nonumber\\\\&=&\dfrac{\sqrt{2-\sqrt{3}}}{2}. \end{eqnarray}
4) Représenter sur le même graphique les points de $a$, $-a$ et $a^{2}$
Exercice 2
On jette trois fois de suite un dé non truqué à six faces portant les chiffres allant de $1$ à $6.$
On lit les numéros des faces supérieures et on les note dans cet ordre $a$, $b$ et $c$.
Puis on forme l'équation du second degré $(E)$ :
$ax^{2}+bxc=0$
1) Soit $A$ l'évènement : $-1\text{est solution de (E) avec } b=6$
Justifions que $p(A)=\dfrac{5}{216}$
Si $-1$ est solution de $(E)$ avec $b=6$ alors $a$ et $c$ vérifient la relation $a+c=6.$
D'où $A=\{(1\;,\ 6\;,\ 5)\ ;\ (2\;,\ 6\;,\ 4)\ ;\ (3\;,\ 6\;,\ 3)\ ;\ (5\;,\ 6\;,\ 1)\ ;\ (4\;,\ 6\;,\ 2)\}$
Ce qui donne
\begin{eqnarray} P(A)&=& 5\times\dfrac{1}{6^{3}}\nonumber\\\\&=&\dfrac{5}{6^{3}}\nonumber\\\\&=&\dfrac{5}{216} \end{eqnarray}
2) La probabilité de l'évènement :
$\surd\ B\ :\ "-2\text{ est solution de }(E)\text{ et }c=4"\text{ est }p(B)=\dfrac{1}{108}$
Justification :
$\text{Si }-2\text{ est solution de }(E)\text{ et }c=4\text{ alors } a\text{ et }b\text{ vérifient la relation }4a-2b+4=0.$
$\text{Ce qui implique que }b=2a+2$
D'où $\boxed{B=\{(1\;,\ 4\;,\ 4)\ ;\ (2\;,\ 6\;,\ 4\}}$
Ce qui donne $p(B)=\dfrac{2}{6^{3}}=\dfrac{1}{108}$
$\surd\ C\ :\ "\text{ la somme des solutions est }-2\text{ et leur produit est }1"\text{ est }p(C)=\dfrac{1}{72}$
Justification :
Si la somme des solutions est $-2$ et leur produit est $1$ alors $a$, $b$ et $c$ vérifient
$$\left\lbrace\begin{array}{lcl} b&=&2a\\ c&=&a \end{array}\right.$$
D'où $\boxed{C=\{(1\;,\ 2\;,\ 1)\ ;\ (2\;,\ 4\;,\ 2)\ ;\ (3\;,\ 6\;,\ 3)\}}$
Ce qui donne $p(C)=\dfrac{3}{6^{3}}=\dfrac{1}{72}$
$\surd\ D\ :\ "\text{ Les deux solutions sont confondues avec }b=4"\text{ est }p(D)=\dfrac{1}{72}$
Justification : si les deux solutions sont confondus avec $b=4$ alors $a$,$b$ et$c$ vérifient
$$\left\lbrace\begin{array}{lcl} b^{2}&=&4ac\\ b&=&4 \end{array}\right.$$
Ce qui implique que $a$ et $c$ vérifient la relation $a\times c=4.$
D'où $\boxed{D=\{(1\;,\ 4\;,\ 4)\ ;\ (2\;,\ 4\;,\ 2)\ ;\ (4\;,\ 4\;,\ 1)\}}$
Ce qui donne $p(F)=\dfrac{3}{6^{3}}=\dfrac{1}{72}$
3) l'épreuve précédente est répétée $10$ fois de suite et de façon indépendante.
a) soit $F$ l'évènement : " l'événement $A$ se réalise une seule fois au $3^{ème}$ essai ".
Montrons que $p(F)=\dfrac{5\times\left(211\right)^{9}}{\left(216\right)^{10}}$
Désignons par $S$ << l'événement $A$ se réalise >> et par $E$ << l'événement $A$ ne se réalise pas >>.
D'où $F$ est le $10-$ couplets définit comme suit : $F=(E\;,\ E\;,\ S\;,\ E\;, \ E\;,\ E\;,\ E\;,\ E\;,\ E\;,\ E).$
Donc $p(F)=C_{1}^{1}\times\dfrac{5}{216}\times\left(\dfrac{211}{216}\right)^{9}$
b) Soit $Y$ la variable aléatoire égale au nombre de réalisations de l'événement $A$ à l'issue des $10$ épreuves.
b-1) La loi de probabilité de $Y$ :
$Y=\{0\;,\ 1\;,\ 2\;,\ 3\;,\ 4\;,\ 5\;,\ 6\;,\ 7\;,\ 8\;,\ 9\:,\ 10\}$
$p(Y=k)=C_{10}^{k}\times\left(\dfrac{5}{216}\right)^{k}\times\left(\dfrac{211}{216}\right)^{10-k}$
Ici $Y$ suit une loi binomiale $B(n\;,\ p)$ de probabilité $p\ ;\ n=10.$
b-2) Le nombre espéré de réalisations de $A$ est :
\begin{eqnarray} E(Y)&=& n\times p(A)\nonumber\\\\&=&10\times\dfrac{5}{216}\nonumber\\\\&=&\dfrac{25}{108} \end{eqnarray}
b-3) La variance de $Y$ est :
\begin{eqnarray} V(Y)&=&n\times p(A)(1-p(A))\nonumber\\\\&=&10\times\dfrac{5}{216}\times\dfrac{211}{216}\nonumber\\\\&=&\dfrac{10550}{(216)^{2}} \end{eqnarray}
Problème :
Partie A
\begin{eqnarray} 1)\quad f(x)\text{ existe }&\Leftrightarrow &\left\lbrace\begin{array}{lllll} 0&<&x&<&1\\ &x&>&0& \end{array}\right.\text{ou}\left\lbrace\begin{array}{lcl} x&\geq &1\\ x&>&0\end{array}\right.\nonumber\\\\&\Leftrightarrow &0<x<1\quad\text{ou}\quad x\geq 1\nonumber\\\\&\Leftrightarrow &x\in\;]0\;,\ +\infty[ \end{eqnarray}
$\boxed{D_{f}=]0\;,\ +\infty[}$
2) $f(1)=1+\dfrac{1}{\sqrt{1}}=1+1=2$,
\begin{eqnarray} \lim\limits_{x\;\longrightarrow\;1^{-}}f(x)&=&\lim\limits_{x\;\longrightarrow\;1^{-}}1+x-x\ln x\nonumber\\\\&=&1+1-1\ln 1\nonumber\\\\&=&2 \end{eqnarray}
\begin{eqnarray} \lim\limits_{x\;\longrightarrow\;1^{+}}f(x)&=&\lim\limits_{x\;\longrightarrow\;1^{+}}1+\dfrac{1}{\sqrt{x}}\nonumber\\\\&=&1+\dfrac{1}{\sqrt{1}}\nonumber\\\\&=&2 \end{eqnarray}
\begin{eqnarray} \lim\limits_{x\;\longrightarrow\;1^{-}}f(x)&=&\lim\limits_{x\;\longrightarrow\;1^{+}}f(x)\nonumber\\\\&=&2 \end{eqnarray}
Donc $\lim\limits_{x\;\longrightarrow\;1}f(x)=2$
$\lim\limits_{x\rightarrow\;1}f(x)=f(1)$
D'où $f$ est continue en 1$1.$
3) Supposons que $0<x<1$
\begin{eqnarray} \dfrac{f(x)-f(x)}{x-1}&=&\dfrac{1+x-x\ln x-2}{x-1}\nonumber\\\\&=&\dfrac{x-1-x\ln x}{x-1}\nonumber\\\\&=&\dfrac{x-1}{x-1}-x\left(\dfrac{\ln x}{x-1}\right)\dfrac{f(x)-f(1)}{x-1}\nonumber\\\\&=& 1-x\left(\dfrac{\ln x}{x-1}\right) \end{eqnarray}
Or $\lim\limits_{x\;\longrightarrow\;1^{-}} x=1\quad\text{et}\quad\lim\limits_{x\;\longrightarrow\;1^{1}}\dfrac{\ln x}{x-1}=1$
\begin{eqnarray} \text{d'où }\lim\limits_{x-1^{-}}\dfrac{f(x)-(1)}{x-1}&=& 1-1(1)\nonumber\\\\&=& 1-1\nonumber\\\\&=& 0 \end{eqnarray}
Donc $f$ est dérivable à gauche en $1$ et $f_{g}^{'}(1)=0.$
Supposons que $x>1$
\begin{eqnarray} \dfrac{f(x)-f(1)}{x-1}&=&\dfrac{1+\dfrac{1}{\sqrt{x}}-2}{x-1}\nonumber\\\\&=&\dfrac{\dfrac{1}{\sqrt{x}}-1}{x-1}\nonumber\\\\&=&\dfrac{1-\sqrt{x}}{\sqrt{x}(x-1)}\nonumber\\\\&=&\dfrac{1-\sqrt{x}}{\sqrt{x}(\sqrt{x-1})(\sqrt{x}+1)}\nonumber\\\\&=&-\dfrac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+1)}\nonumber\\\\&=&\dfrac{1}{\sqrt{x}(\sqrt{x}+1)}\nonumber\\\\\text{d'où}\lim\limits_{x\rightarrow\;1^{+}}\dfrac{f(x)-f(1)}{x-1}\nonumber\\\\&=&-\dfrac{1}{\sqrt{1}(\sqrt{1}+1)}\nonumber\\\\&=&-\dfrac{1}{2} \end{eqnarray}
Donc $f$ est dérivable à droite en $1$ et $f_{\mathrm{d}}^{\prime}(1)=-\dfrac{1}{2}$
$f_{\mathrm{d}}^{\prime}(1)\neq\;f_{g}^{\prime}(1)$ ; donc $f$ n'est pas dérivable en $1$
$f_{g}^{\prime}(1)=0$ ; donc $\left(\mathcal{C}_{f}\right)$ admet au point d'abscisse $1$ une demi-tangente horizontale à gauche.
$f_{\mathrm{d}}^{\prime}(1)=-\dfrac{1}{2}$ ; donc $\left(\mathcal{C}_{f}\right)$ admet au point d'abscisse $1$ une demi-tangente oblique de coefficient directeur $-\dfrac{1}{2}$ à droite.
4) $\lim\limits_{x\;\longrightarrow\;0^{+}}1+x=1+0=0$ ;
$\lim\limits_{x\;\longrightarrow\;0^{+}}x\ln x=0$ ;
$\lim\limits_{x\;\longrightarrow\;0^{+}}f(x)=1.$
$\lim\limits_{x\;\longrightarrow\;+\infty}\sqrt{x}=+\infty$ ;
$\lim\limits_{x\;\longrightarrow\;+\infty}\dfrac{1}{\sqrt{x}}=0$ ;
$\lim\limits_{x\;\longrightarrow\;+\infty}f(x)=1$
$\lim\limits_{x\;\longrightarrow\;+\infty}f(x)=1$, donc la droite d'équation $y=1$ est une asymptote horizontale à $\left(\mathcal{C}_{f}\right)$ en $+\infty.$
5) $0\not\in\;D_{f}$ et $\lim\limits_{x\;\longrightarrow\;0^{+}}f(x)=1\in\mathbb{R}$ ; donc $f$ admet un prolongement par continuité à droite en $0.$
$$\left\lbrace\begin{array}{lcl} h(x)&=&f(x)\quad\text{si }x>0\\ h(0)&=&1 \end{array}\right.$$
6) Supposons que $0<x<1.$
$\begin{array}{lcl} \dfrac{h(x)-h(0)}{x-0}&=&\dfrac{1+x-x\ln x-1}{x}\\\\&=&\dfrac{x-x\ln x}{x}\\\\&=&\dfrac{x(1-\ln x)}{x}\\\\&=&1-\ln x. \end{array}$
$\lim\limits_{x\;\longrightarrow\;0^{+}}\dfrac{h(x)-h(0)}{x-0}=\lim\limits_{x\;\longrightarrow\;0^{+}}1-\ln x$ ;
$\lim\limits_{x\;\longrightarrow\;0^{+}}\ln x=-\infty$
$\Rightarrow\lim\limits_{x\;\longrightarrow\;0^{+}}-\ln x=+\infty.$
$\lim\limits_{x\;\longrightarrow\;0^{+}}\dfrac{h(x)-h(0)}{x-1}=+\infty$ ; donc $h$ n'est pas dérivable à droite en $0$
La courbe de $h$ admet au point d'abscisse $0$ une demi-tangente verticale à droite.
7) $\begin{array}{lcl} \forall\;x\in\;]0\;,\ 1[\;,\ f^{\prime}(x)&=&1-\left(\ln x+x\times\dfrac{1}{x}\right)\\\\&=&1-\ln x-1\\\\&=&-\ln x. \end{array}$
$\begin{array}{lcl} \forall\;x\in\;]0\;,\ +\infty[\;,\ f^{\prime}(x)&=&-\dfrac{\dfrac{1}{2\sqrt{x}}}{\left(\sqrt{x}\right)^{2}}\\\\&=&-\dfrac{1}{2x\sqrt{x}} \end{array}$
$\begin{array}{lcl} \forall\;x\in\;]0\;,\ 1[\;,\ \ln x<0&\Rightarrow&-\ln x>0\\\\&\Rightarrow&f^{\prime}(x)>0. \end{array}$
$\forall\;x\in\;]1\;,\ +\infty[x\sqrt{x}>0\Rightarrow\;f^{\prime}(x)<0.$
$$\begin{array}{|c|lcccr|} \hline x&0& &1& &+\infty\\ \hline f^{\prime}(x)&|&+&||&-& \\ \hline &|& &2& &\\ f&|&\nearrow& &\searrow&\\ &1& &&&1 \\\hline \end{array}$$
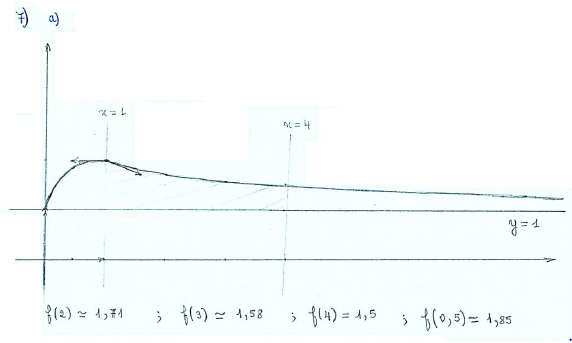
$$\text{b) }A=\int_{1}^{4}[f(x)-1]\mathrm{d}x\times U.a\;,\text{ avec }U.a=\text{ unité d'aire}.$$
\begin{eqnarray} \text{On a }:\ \int_{1}^{4}[f(x)-1]\mathrm{d}x&=&\int_{1}^{4}\left(1+\dfrac{1}{\sqrt{x}}-1\right)\mathrm{d}x\nonumber\\\\&=&\int_{1}^{4}\dfrac{1}{\sqrt{x}}\mathrm{d}x\nonumber\\\\&=&\left[2\sqrt{x}\right]_{1}^{4}\nonumber\\\\&=&2\sqrt{4}-2\sqrt{1}\nonumber\\\\&=&2. \end{eqnarray}
Or $1\;U.a=2\,cm\times2\,cm=4\,cm^{2}.$
$\boxed{\text{Donc}A=2\times 4\,cm^{2}=8\,cm^{2}.}$
3.1) $g=f\text{ sur }[1\;,\ +\infty[.$
\begin{eqnarray} \text{a }g(x)&=&x\nonumber\\\\\Leftrightarrow\;g(x)-x&=&0\nonumber\\\\\Leftrightarrow\;k(x)&=&0\;,\nonumber\\\\\text{ avec }k(x)&=&g(x)-x. \end{eqnarray}
$k$ est dérivable sur $]1\;,\ +\infty[.$
\begin{eqnarray} \forall\;x\in]1\;,\ +\infty[\;,\ k^{\prime}(x)&=&g^{\prime}(x)-1\nonumber\\\\&=&f^{\prime}(x)-1\nonumber\\\\&=&-\dfrac{1}{2x\sqrt{x}}-1. \end{eqnarray}
$\forall\,x\in]1\;,\ +\infty[\;,\ k^{\prime}(x)<0\;,\text{ donc }k\text{ est stricement décroissance sur }]1\;,\ +\infty[.$
$\text{donc}k\text{ est une bijection de }[1\;,\ +\infty[\text{ sur }k([1\;,\ +\infty[)=\left]\lim\limits_{x\;\longrightarrow\;+\infty}k(x)\;,\ k(1)\right]=]-\infty\;,\ 1].$
$\text{Or }0\in]-\infty\;,\ 1]\;,\text{ donc l'équation }k(x)=0\text{ admet une unique solution }\alpha\text{ dans }[1\;,\ +\infty[.$
$\text{En conséquence l'équation }g(x)=x\text{ admet une unique solution }\alpha\text{ dans }[1\;,\ +\infty[.$
$k(1)=1$ ;
\begin{eqnarray} k(2)&=&g(2)-2\nonumber\\\\&=&f(2)-2\simeq\;1.71-2\simeq\;-0.29 \end{eqnarray}
$k((1)\times\;k(2)<0\Rightarrow \;1<\alpha<2.$
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|} \hline x&1&1.1&1.2&1.3&1.4&1.5&1.6&1.7&1.8&1.9&2\\ \hline k(x)&1&&&&&0.32&0.19&0.06&-0.05&-0.37&-0.29\\ \hline \end{array}$$
$k(1.5)=f(1.5)-1.5\simeq 0.32$ ;
$k(1.6)=f(1.6)-1.6\simeq 0.19$ ;
$k(1.7)=f(1.7)-1.7\simeq 0.06$ ;
$k(1.8)=f(1.8)-1.8\simeq -0.05.$
$k(1.7)\times k(1.8)<0\Rightarrow\;1.7<\alpha<1.8.$
\begin{eqnarray} \text{b.}\quad\forall\;x\in\;[1\;,\ +\infty[\;,\ g^{\prime}(x)&=&-\dfrac{1}{2x\sqrt{x}}\nonumber\\\\\Rightarrow\;\left|g^{\prime}(x)\right|&=&\left|-\dfrac{1}{2x\sqrt{x}}\right|\nonumber\\\\&=&\dfrac{1}{2x\sqrt{x}} \end{eqnarray}
$\begin{array}{lll} x\in\;[1\;,\ +\infty[ &\Rightarrow&\;x\geq 1\\\\ &\Rightarrow&\sqrt{x}\geq \sqrt{1}\\\\&\Rightarrow&\sqrt{x}\geq 1\\\\&\Rightarrow&\;x\sqrt{x}\geq x\\\\&\Rightarrow&\;x\sqrt{x}\geq\;1\\\\&\Rightarrow&\;2x\sqrt{x}\geq\;2\\\\&\Rightarrow&\dfrac{1}{2x\sqrt{x}}\leq\dfrac{1}{2}\\\\&\Rightarrow&\left|g^{\prime}(x)\right|\leq\dfrac{1}{2}. \end{array}$
c. $g$ est dérivable sur $[1\;,\ +\infty[$
$\forall\;t\in\;[1\;, +\infty[\;,\ \left|g^{\prime}(t)\right|\leq\dfrac{1}{2}.$
$\text{Or }\alpha\in\;[1\;,\ +\infty[$ ;
$\text{donc }\forall\;x\in[1\;,\ +\infty[\;,\ \left|g(x)-g(\alpha)\right|\leq\dfrac{1}{2}|x-\alpha|$
$\Rightarrow\;|g(x)-\alpha|\leq\dfrac{1}{2}|x-\alpha|.$
2.a.$w_{0}=2.$
$\text{Or }2\geq\;1$ ;
$\text{donc }w_{0}\geq\;1.$
$\text{Supposons que }w_{n}\geq\;1\;,n\geq\;0\text{ et montons que }w_{n+1}\geq\;1.$
\begin{eqnarray} w_{n}\geq\;1&\Rightarrow &\dfrac{1}{\sqrt{w}_{n}}>0\nonumber\\\\&\Rightarrow &1+\dfrac{1}{\sqrt{w}_{n}}>1\nonumber\\\\&\Rightarrow &w_{n+1}>1\nonumber\\\\&\Rightarrow &w_{n+1}\geq\;1. \end{eqnarray}
$\boxed{\text{D'où }\forall\;n\in\mathrm{N}\;,w_{n}\geq\;1}.$
$\text{b. }\forall\;x\in[1\;,\ +\infty[\;,|g(x)-\alpha|\leq\dfrac{1}{2}|x\;\ -\alpha|.$
Or d'après la question précédente, $w_{n}\geq\;1.$
Ce qui implique que $w_{n}\in\;[1\;,\ +\infty[.$
\begin{eqnarray} w_{n}\in[1\;,\ +\infty[ &\Rightarrow &\left|g\left(w_{n}\right)-\alpha\right|\leq\dfrac{1}{2}\left|w_{n}-\alpha\right|\nonumber\\\\&\Rightarrow &\left|w_{n+1}-\alpha\right|\leq\dfrac{1}{2}\left|w_{n}-\alpha\right|. \end{eqnarray}
c. $\left(\dfrac{1}{2}\right)^{0}\left|w_{0}-\alpha\right|=\left|w_{0}-\alpha\right|.$
Or $\left|w_{0}-\alpha\right|\leq\left|w_{0}-\alpha\right|$,
Donc $\left|w_{0}-\alpha\right|\leq\left(\dfrac{1}{2}\right)^{0}\left|w_{0}-\alpha\right|.$
Supposons que $\left|w_{n}-\alpha\right|\leq\left(\dfrac{1}{2}\right)^{n}\left|w_{0}-\alpha\right|\;,\ n\geq\;0$ et montrons que $\left|w_{n+1}-\alpha\right|\leq\left(\dfrac{1}{2}\right)^{n+1}\left|w_{0}-\alpha\right|.$
$\left|w_{n+1}-\alpha\right|\leq\dfrac{1}{2}\left|w_{n}-\alpha\right|.$
Or $\left|w_{n}-\alpha\right|\leq\left(\dfrac{1}{2}\right)^{n}\left|w_{0}-\alpha\right|$,
Donc $\left|w_{n+1}-\alpha\right|\leq\dfrac{1}{2}\times\left(\dfrac{1}{2}\right)^{n}\left|w_{0}-\alpha\right|$
$\Rightarrow\left|w_{n+1}-\alpha\right|\leq\left(\dfrac{1}{2}\right)^{n+1}\left|w_{0}-\alpha\right|.$
D'où $\forall\;n\in\mathbb{N}\;,\ \left|w_{n}-\alpha\right|\leq\left(\dfrac{1}{2}\right)^{n}\left|w_{0}-\alpha\right|.$
$\begin{array}{lll} \lim\limits_{x\;\longrightarrow\;+\infty}\left(\dfrac{1}{2}\right)^{n}&=&0\\\\\Rightarrow\lim\limits_{x\;\longrightarrow\;+\infty}\left(\dfrac{1}{2}\right)^{n}\left|w_{0}-\alpha\right|&=&0\\\\\Rightarrow\lim\limits_{x\;\longrightarrow\;+\infty}\left|w_{n}-\alpha\right|&=&0\\\\\Rightarrow\lim\limits_{x\;\longrightarrow\;+\infty}\;w_{n}&=&\alpha. \end{array}$

Ajouter un commentaire