Corrigé Bac Maths S2 1er groupe 2016

1. a. Soit $\alpha$ une solution réelle de $(E)$ alors $\alpha$ vérifie $\alpha^{3}-13\alpha^{2}+59\alpha-87=0$.

Une solution évidente est 3.

D'où $$\boxed{\alpha=3}$$

 

1. b. $(z-3)(z^{2}-10z+29)=0$.

D'où $z=3\text{ ou }z^{2}-10z+29=0$.

Après calculs $z=3\text{ ou }z=5-2\mathrm{i}\text{ ou }z=5+2\mathrm{i}$.

L'ensemble des solutions est : $S=\{3;\ 5-2\mathrm{i};\ 5+2\mathrm{i}\}$.

 

2. a $\dfrac{b-a}{c-a}=-\mathrm{i}$.

$$\left\{\begin{array}{lcl}arg\left(\dfrac{b-a}{c-a}\right)&\equiv&  -\dfrac{\pi}{2}\Leftrightarrow(\overrightarrow{AC},\ \overrightarrow{AB})\equiv -\dfrac{\pi}{2}\;[2\pi]\\\\AB &=& AC\end{array}\right.$$

$ABC$ est rectangle et isocèle en $A$ et direct.

 

2. b. $\boxed{Arg\;Z\equiv(\overrightarrow{MB},\ \overrightarrow{MA})\ [2\pi]}$.

 

$Z$ réel non nul si et seulement si $arg\;Z\equiv 0\ (\pi)$.

$(\overrightarrow{MB},\ \overrightarrow{MA})\ (\pi)$.

M décrit la droite $(AB)$ privée de $A$ et de $B$.

 

3. a. Soit $M'(Z')$ l'image de $M(Z)$ par la rotation $r$ de centre $I$ et d'angle $-\dfrac{\pi}{2}$

Donc $Z'-Z_{i}=\mathrm{e}^{-\frac{\pi}{2}}(Z-Z_{i})$.

On obtient $\boxed{Z'=-\mathrm{i}Z+3+\mathrm{i}}$

 

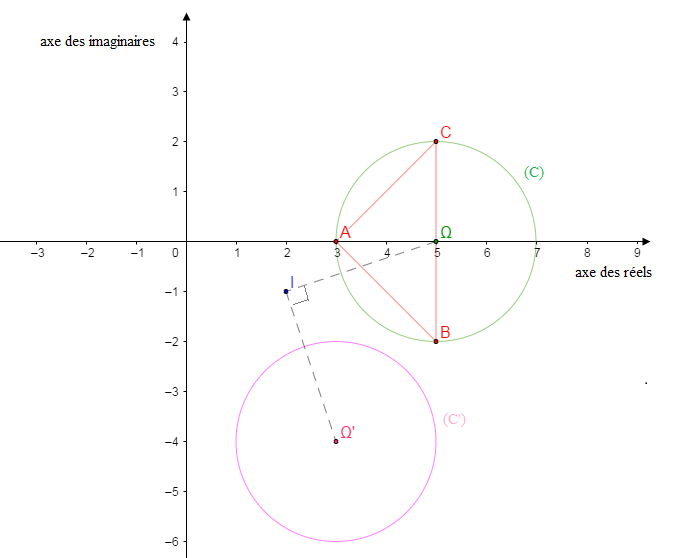
3. b. Soit $\Omega$ centre du cercle circonscrit à $ABC$.

$\Omega$ est le milieu de $[BC]$.

On a $Z_{\Omega}=\dfrac{Z_{B}+Z_{C}}{2}$

ce qui donne $\boxed{Z_{\Omega}=5}$.

 

Soit $r(\Omega)=\Omega'\;,\ Z_{\Omega'}=-\mathrm{i}Z_{\Omega}+3+\mathrm{i}$. D'où $\boxed{Z_{\Omega'}=3-4\mathrm{i}}$.

Donc $(\mathcal{C}')$ est le cercle de centre $\Omega'$ et de même rayon que $(\mathcal{C})$.

 

 

1. $p(A)=\dfrac{C_{4}^{2}}{C_{5}^{2}}\qquad\boxed{p(A)=\dfrac{3}{5}}$.

$p(B)=\dfrac{C_{4}^{1}\times C_{1}^{1}}{C_{5}^{2}}\qquad\boxed{p(B)=\dfrac{2}{5}}$.

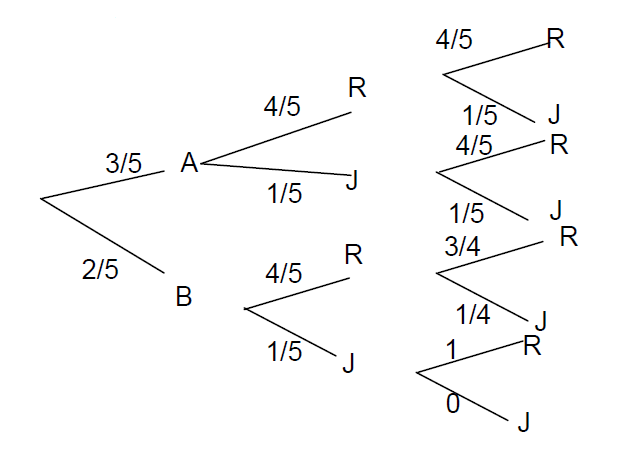
$p(C)=\dfrac{4}{5}\times\dfrac{4}{5}+\dfrac{1}{5}\times\dfrac{1}{5}\qquad \boxed{p(C)=\dfrac{17}{25}}$.

 

$p(D)=\dfrac{4}{5}\times\dfrac{3}{4}\qquad \boxed{p(D)=\dfrac{3}{5}}$.

 

$p(E)=\dfrac{4}{5}\times\dfrac{1}{4}+\dfrac{1}{5}\times 1\qquad \boxed{p(E)=\dfrac{2}{5}}$.

 

$p(F)=\dfrac{2}{5}\times\dfrac{4}{5}\times\dfrac{1}{4}+\dfrac{2}{5}\times\dfrac{1}{5}\times 1\qquad \boxed{p(F)=\dfrac{4}{25}}$.

 

 

2.a. $X(\Omega)=\{(R,\ R),\ (R,\ J),\ (J,\ R),\ (J,\ J)\}$ Les différentes valeurs prises par X sont 0; 1000 et 2000.

$$\begin{array}{|c|c|c|c|}\hline a & 0 & 1000 & 2000\\ \hline P(X=a) & \frac{3}{125} & \frac{44}{125} & \frac{78}{125}\\\hline\end{array}$$

 

b. Fonction de répartition

$-\ $ si $x<0$, $F(x)=0$.

$-\ $ si $0\leq x<1000$, $F(x)=\dfrac{3}{125}$

$-\ $ si $1000\leq x<2000$, on a $F(x)=\dfrac{3}{125}+\dfrac{44}{125}$.

D'où si $1000\leq x<2000$,  $\boxed{F(x)=\dfrac{47}{125}}$

$-\ $ si $x\geq 2000\  F(x)=\dfrac{3}{5}+\dfrac{44}{125}+\dfrac{78}{125}=1$

 

3. $\boxed{p(G)=\left(\dfrac{78}{125}\right)^{50}}\quad\boxed{p(H)=\left(\dfrac{3}{125}\right)^{50}}\quad\boxed{p(I)=\left(\dfrac{44}{125}\right)^{50}+C_{50}^{25}\left(\dfrac{3}{125}\right)^{25}\left(\dfrac{78}{125}\right)^{25}}$

Partie A

 

1. a. $g(x)$ existe si et seulement si: $\left\{\begin{array}{lcl}x+1 &>& 0\\x+1 &\neq& 0\end{array}\right.$

ce que donne $x>-1$.

 

$\boxed{Dg=]-1,\ +\infty[}$.

 

$$\lim_{x\rightarrow -1^{+}}\dfrac{-2(x+1)\ln(x+1)+x}{(x+1)}$$ ,

 

$\boxed{\lim_{x\rightarrow -1^{+}}g(x)=-\infty}$ par quotient

 

$\lim_{x\rightarrow +\infty}g(x)=-\infty$ car  $\left\{\begin{array}{lll}-2\ln(x+1)\rightarrow -\infty\text{ par composée puis produit }\\\\\dfrac{x}{x+1}\rightarrow 1 \end{array}\right.$

 

1. b. $g'(x)=\dfrac{-2}{x+1}+\left(\dfrac{x}{x+1}\right)'\quad\boxed{g'(x)=\dfrac{-2x-1}{(x+1)^{2}}}$

$$\begin{array}{|c||lcccr|}\hline x & -1 & & -\frac{1}{2} & & +\infty\\\hline g'(x) & & + & 0 & - &  \\\hline \end{array}$$

 

 

Tableau de Variation

 

$$\begin{array}{|c||lcccr|}\hline x & -1 & & -\frac{1}{2} & & +\infty\\\hline g'(x) &  & + & 0 & - & \\\hline g &  & \nearrow & 2\ln 2-1 & \searrow & \\& -\infty &  &  &  & -\infty \\\hline \end{array}$$

 

2. a. $g(0)= 0$.

La restriction de $g$ à $]-1;\ -\frac{1}{2}$ est strictement croissante et continue et prend ses valeurs dans $]-\infty,\  2ln 2-1[$ qui contient donc l'équation $g(x)=0$ admet sur $]-1;\ -\frac{1}{2}$

une solution unique $\alpha$.

Idem sur $]-\frac{1}{2};\ +\infty[$, l'équation $g(x)=0$ admet un solution unique 0 .

$]-0.72;\ -0.71[\subset]-1;\ -\frac{1}{2}[$

et $g(-0.72)\times g(-0.71)<0$ donc $\alpha\in]-0.72;\ -0.71[$.

 

2. b. 0 étant l'autre zéro de $g$ :

$$\begin{array}{|c||lcccccr|}\hline x & -1 &  & \alpha &  & 0 &  & +\infty\\\hline g(x) &  & - & 0 & + & 0 & - &  \\\hline\end{array}$$

 

Partie B

 

1. a. Domaine de définition de $f$.

$f(x)$ existe si et seulement si: $\left\{\begin{array}{lcl}x+1 &>& 0\\\ln(x+1) &\neq& 0\end{array}\right.$

 

- ou $x\in]-\infty,\ -1]$,

- ou $x=0$

 

d'où $\left\{\begin{array}{lcl}x &>& -1\\x &\neq& 0\end{array}\right.$ ou $x\in]-\infty,\ -1]$ ou $x=0$

 

$D_{f}=(]-1,\ +\infty\setminus\{0\})\cup]-\infty,\ -1]\cup\{0\}$

 

$$\boxed{D_{f}=\mathbb{R}}$$

 

Limites aux bornes du domaine de définition de $f$.

$$\lim_{x\rightarrow -\infty}f(x)=-\infty;\ \lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\dfrac{x^{2}}{x+1}\times\dfrac{(x+1)}{\ln(x+1)}=+\infty$$ ,

 

$\lim_{x\rightarrow +\infty}f(x)=+\infty$

 

1.b. Étudions la nature de la branche infinie au voisinage de $-\infty$ .

 

$$\lim_{x\rightarrow -\infty}\dfrac{f(x)}{x}=\lim_{x\rightarrow -\infty}\left(\dfrac{x+1}{x}\right)\mathrm{e}^{-x-1}=+\infty$$

 

$$\lim_{x\rightarrow -\infty}\dfrac{f(x)}{x}=+\infty$$

 

Donc $(\mathcal{C}_{f})$ admet au voisinage de $-\infty$ une branche parabolique de direction celle de l'axe des ordonnées

Étudions la nature de la branche infinie au voisinage de $+\infty$.

 

$$\lim_{x\rightarrow +\infty}\dfrac{f(x)}{x}=\lim_{x\rightarrow +\infty}\left(\dfrac{x}{x+1}\right)\dfrac{(x+1)}{\ln(x+1)}=+\infty$$

 

Donc $(\mathcal{C}_{f})$ admet au voisinage de $-\infty$ une branche parabolique de direction celle de l'axe des ordonnées

 

2. a.

$f(-1)=0$.

 

$$\lim_{x\rightarrow -1^{+}}f(x)=0\text{ par quotient et }\lim_{x\rightarrow -1^{-}}f(x)=f(-1)=0$$

 

D'où $$\boxed{\lim_{x\rightarrow -1^{+}}f(x)=\lim_{x\rightarrow -1^{-}}f(x)=f(-1)=0}$$  

 

Donc est continue en -1.

 

On a $f(0)=0$

 

$$\lim_{x\rightarrow 0}f(x)=\lim_{x\rightarrow 0}x\times\dfrac{x}{\ln(x+1)}=0$$

 

D'où $$\boxed{\lim_{x\rightarrow 0}f(x)=f(0)}$$

 

Donc est continue en 0.

 

2. b. Dérivabilité de $f$ en -1.

 

$$\lim_{x\rightarrow -1^{-}}\dfrac{f(x)-f(-1)}{x+1}=\lim_{x\rightarrow -1}\dfrac{(x+1)}{(x+1)}\mathrm{e}^{-x-1}=1$$

 

$f$ dérivable en -1 à gauche et $\boxed{f'_{g}(-1)=1}$ 

$$\lim_{x\rightarrow -1^{+}}\dfrac{f(x)-f(-1)}{x+1}=\lim_{x\rightarrow -1^{+}}\dfrac{x^{2}}{(x+1)\ln(x+1)}=-\infty$$

 

Donc non dérivable en -1 car non dérivable en -1 à droite.

 

Interprétation point d'abscisse -1.

Au point d'abscisse -1 $(\mathcal{C}_{f})$ admet une demi-tangente verticale et une demi- tangente de pente 1 à gauche.

 

Dérivabilité de $f$ en 0.

$$\lim_{x\rightarrow 0}\dfrac{f(x)-f(0)}{x-0}=\lim_{x\rightarrow 0}\dfrac{x}{\ln(x+1)}=1$$

 

Donc est dérivable en 0 et $f'(0)=1$.

 

Interprétation au point d'abscisse 0.

$(\mathcal{C}_{f})$ admet à l'origine une tangente de coefficient directeur 1.

 

3. a. Pour tout $x\in]-1,\ +\infty[\setminus\{0\}$ on a $$f'(x)=\left(\dfrac{x^{2}}{\ln(x+1)}\right)'=\dfrac{2x\ln(x+1)-\dfrac{x^{2}}{x+1}}{(\ln(x+1))^{2}}=\dfrac{-x(-2\ln(x+1)+\dfrac{x}{x+1})}{(\ln(x+1))^{2}}$$

 

$$\boxed{f'(x)=\dfrac{-xg(x)}{(\ln(x+1))^{2}}}$$

 

Pour $x<-1$, $\ f'(x)=-x\mathrm{e}^{-x-1}$

 

3. b. 

 

$$\begin{array}{|c|lcccccr|}\hline x  & -\infty &  & -1 &  & \alpha & 0 & +\infty \\\hline f'(x) &  & + & || & - & 0  & +  &   \\\hline f  &   &   & 0 &   &   & 0  & +\infty   \\&   & \nearrow &   &\searrow &  &  \nearrow &     \\& -\infty &   &   &   & f(\alpha) &  &   \\\hline\end{array}$$

 

 

4. a $h$ est continue et strictement croissante sur $[0,\ +\infty[$, elle réalise donc une bijection de $[0,\ +\infty[$ vers $[0,\ +\infty[=J$

 

4. b. $h^{-1}$ a le même sens de variation que , elle est strictement croissante sur $J$.

 

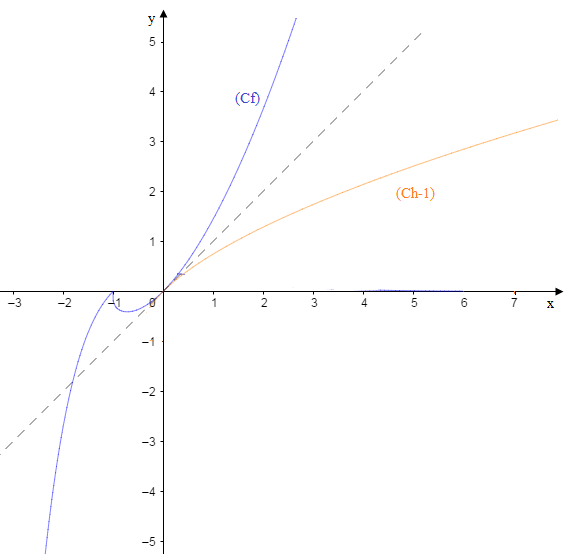
4. c. Figure :

 

Partie C

 

1. a. Posons $u'(x)=\dfrac{1}{x^{2}}\text{ et }v'(x)=\dfrac{1}{x+1}$ avec $u(x)=-\dfrac{1}{x}\text{ et }v(x)=\ln(x+1)$.

 

Sur $]0,\ +\infty[$, on a $m(x)=\dfrac{1}{x^{2}}\ln(x+1)+\left(-\dfrac{1}{x}\right)\left(\dfrac{1}{x+1}\right).\qquad(R)$

 

1. b. On a $m(x)=(u(x)v(x))'$.

Pour tout $x\in]0,\ +\infty[$ on a $H'(x)=m(x)$ avec $m(x)=(u(x)v(x))'$.

D'où on a : $H(x)=u(x)v(x)+c=-\dfrac{\ln(x+1)}{x}+c$.

On a sur $x\in]0,\ +\infty[\;,\ \dfrac{1}{f(x)}=\dfrac{\ln(x+1)}{x^{2}}$ on ’ m e m ’

Or d'après $(R)$ : $\dfrac{\ln(x+1)}{x^{2}}=m(x)+\dfrac{1}{x}\times\dfrac{1}{x+1}=m(x)+\dfrac{1}{x}-\dfrac{1}{x+1}$.

Soit $G$ une primitive de la fonction $x\rightarrow \dfrac{\ln(x+1)}{x^{2}}$.

 

 

$\int_{1}^{2}\frac{1}{f(x)}\mathrm{d}x=\left\lbrack G(x)\right\rbrack_{1}^{2}=\left\lbrack H(x)+\ln\left(\dfrac{x}{x+1}\right)\right\rbrack_{1}^{2}=\left\lbrack-\dfrac{\ln(x+1)}{x}+c+\ln\left(\dfrac{x}{x+1}\right)\right\rbrack_{1}^{2}=-\dfrac{3\ln 2}{2}+3\ln 2$

 

$\int_{1}^{2}\frac{1}{f(x)}\mathrm{d}x=3(\ln 2-\ln\sqrt{3})=3\ln\left(\dfrac{2\sqrt{3}}{3}\right)$

Source: Office du Bac Sénégal