Corrigé Bac Maths S1 S3 1er groupe 2008
Exercice 1
1) En désignant par $b$ le terme central de la progression arithmétique et par $r$ sa raison, on peut écrire : $a=b-r$ et $c=b+r.$
Les autre données se traduisent alors par :
$$\left\lbrace\begin{array}{lcr}\sum_{k\in\;\{-1\;,\ 1\;,\ 2\}}p(X=k) &=& 1 \\ \\ E(X) &=& 1 \end{array}\right.$$
c'est à dire $\left\lbrace\begin{array}{lcr}\mathrm{e}^{a}+\mathrm{e}^{b}+\mathrm{e}^{c} &=& 1 \\ 1.\mathrm{e}^{a}-1.\mathrm{e}^{b}+2.\mathrm{e}^{c} &=& 1 \end{array}\right.\quad\text{soit}\quad\left\lbrace\begin{array}{lcr}\mathrm{e}^{b}\mathrm{e}^{-r}+\mathrm{e}^{b}+\mathrm{e}^{b}\mathrm{e}^{r} &=& 1 \\ \mathrm{e}^{b}\mathrm{e}^{-r}-\mathrm{e}^{b}+2.\mathrm{e}^{b}\mathrm{e}^{r} &=& 1\end{array}\right.$
En faisant la différence membre à membre et en simplifiant par $\mathrm{e}^{b}$, on trouve $\mathrm{e}^{r}=2$ soit $r=\ln 2.$
La première équation devient alors :
$\left(\dfrac{1}{2}+1+2\right)$ c'est à dire $\ \mathrm{e}^{b}=\dfrac{2}{7}\ \Rightarrow\ b=\ln\dfrac{2}{7}$
Ensuite $a=b-r=\ln\dfrac{2}{7}-\ln 2\ \Rightarrow\ a=\ln\dfrac{1}{7}$
Et $c=b+r=\ln\dfrac{2}{7}+\ln 2\ \Rightarrow\ c=\ln\dfrac{4}{7}$
Pour calculer la variance, calculons d'abord $E(X^{2}).$
\begin{eqnarray} E(X^{2}) &=& 1^{2}.\mathrm{e}^{a}+(-1)^{2}.\mathrm{e}^{b}+2^{2}.\mathrm{e}^{c} \nonumber \\ &=& \dfrac{1}{7}+\dfrac{2}{7}+4\dfrac{4}{7} \nonumber \\ &=& \dfrac{19}{7} \nonumber \end{eqnarray}
Alors
\begin{eqnarray} V(X) &=& E(X^{2})-(E(X))^{2} \nonumber \\ &=& \dfrac{19}{7}-1 \nonumber \\ \Rightarrow\ V(X) &=& \dfrac{12}{7} \nonumber \end{eqnarray}
2) a) $x_{G}=\dfrac{1}{7}(1.x_{A}+2x_{B}+4x_{C})=1$ donc $G=A$
b) $\varphi(G)=\dfrac{1}{7}[\overrightarrow{GA}^{2}+2\overrightarrow{GB}^{2}+4\overrightarrow{GC}^{2}]$
Soit, en se souvenant que $G=A\ :$
\begin{eqnarray} \varphi(G) &=& \dfrac{1}{7}[2\overrightarrow{AB}^{2}+4\overrightarrow{AC}^{2}] \nonumber \\ &=& \dfrac{1}{7}(2.4+4.1) \nonumber \\ \Rightarrow\ \varphi(G) &=& \dfrac{12}{7} \nonumber \\ &=& V(X) \nonumber \end{eqnarray}
On peut écrire en utilisant la relation de Schales et en développant :
\begin{eqnarray} \varphi(M) &=& \dfrac{1}{7}[(\overrightarrow{MG}+\overrightarrow{GA})^{2}+2(\overrightarrow{MG}+\overrightarrow{GB})^{2}+4(\overrightarrow{MG}+\overrightarrow{GC})^{2}] \nonumber \\ &=& \dfrac{1}{7 }[\overrightarrow{MG}^{2}+\overrightarrow{GA}^{2}+2\overrightarrow{MG}.\overrightarrow{GA}+2(\overrightarrow{MG}^{2}+\overrightarrow{GB}^{2}+2\overrightarrow{MG}.\overrightarrow{GB})+4(\overrightarrow{MG}^{2}+\overrightarrow{GC}^{2}+2\overrightarrow{MG}.\overrightarrow{GC})] \nonumber \\ &=& \overrightarrow{MG}^{2}+\dfrac{1}{7}[\overrightarrow{GA}^{2}+2\overrightarrow{GB}^{2}+4\overrightarrow{GC}^{2}]+\dfrac{1}{7}.2\overrightarrow{MG}[\overrightarrow{GA}+2\overrightarrow{GB}+4\overrightarrow{GC}] \nonumber \end{eqnarray}
Le troisième du second membre est nul parce que $G$ est le barycentre du système $\{(A\;,\ 1)\;,\ (B\;,\ 2)\;,\ (C\;,\ 4)\}.$
Donc, $\varphi(M)=\overrightarrow{MG}^{2}+\varphi(G)$
La relation $\varphi(G)=3$ est alors équivalente à : $\overrightarrow{MG}^{2}=\dfrac{9}{7}$ ou $MG=3\dfrac{\sqrt{7}}{7}$
Par conséquent
$(\Gamma)=\{M_{1}\;,\ M_{2}\}$ où $M_{1}$ et $M_{2}$ sont les deux points de $(\Delta)$ dont la distance au point $A$ est $-3\dfrac{\sqrt{7}}{7}$ et $3\dfrac{\sqrt{7}}{7}$
Exercice 2
1) a) On a, pour tout réel $x$ compris entre $k$ et $k+1\ :\ \dfrac{1}{k+1}\leq\dfrac{1}{x}\leq\dfrac{1}{k}.$
Puis en intégrant : $$\int_{k}^{k+1}\dfrac{1}{k+1}\mathrm{d}x\leq\int_{k}^{k+1}\mathrm{d}x\leq\int_{k}^{k+1}\dfrac{1}{x}\dfrac{1}{k}\mathrm{d}x$$
c'est à dire $$\dfrac{1}{k+1}\leq \int_{k}^{k+1}\dfrac{1}{x}\mathrm{d}x\leq\dfrac{1}{k+1}$$
b)
\begin{eqnarray}\int_{k}^{k+1}\dfrac{1}{x}\mathrm{d}x &=& [\ln x]_{k}^{k+1} \nonumber \\ &=& \ln(k+1)-\ln k \nonumber \\ &=& \ln\dfrac{k+1}{k} \nonumber \\ &=& \dfrac{1}{k}-f(k) \nonumber \end{eqnarray}
2) a) En réduisant le deuxième membre au même dénominateur, on obtient : $$\dfrac{a}{x}+\dfrac{b}{x+1}=\dfrac{(a+b)x+a}{x(x+1)}$$
Donc $a$ et $b$ sont tels que $\forall\;x\neq 0\ \text{ et }\ -1.$
Alors $a+b=0$ et $a=1$; ce qui entraîne $b=-1$
Par conséquent $\dfrac{1}{x(x+1)}=\dfrac{1}{x}-\dfrac{1}{x+1}$
b) Soit
\begin{eqnarray} U_{n} &=& \sum_{k=n}^{2n}\dfrac{1}{k(k+1)} \nonumber \\ &=& \sum_{k=n}^{2n}\left[\dfrac{1}{k}-\dfrac{1}{k+1}\right] \nonumber \\ &=& \sum_{k=n}^{2n}[\alpha_{k}-\alpha_{k+1}]\quad\text{avec }\ \alpha_{k}=\dfrac{1}{k} \nonumber \end{eqnarray}
Donc en procédant à une itération :
$$U_{n}=\alpha_{n}-\alpha_{2n+1}=\dfrac{n+1}{n(2n+1)}$$
Ensuite $$\lim_{n\mapsto +\infty}U_{n}=0$$
c) Dans les inégalités de la question 1) a), remplaçons l'intégrale par sa valeur tirée de la question 1) b) $\dfrac{1}{k+1}\leq\dfrac{1}{k}-f(k)\leq\dfrac{1}{k}.$
ce qui permet d'encadrer $f(k)\ :$
$$0\leq f(k)\leq\dfrac{1}{k}-\dfrac{1}{k+1}$$
Puis sommons membre à membre ces inégalités depuis $k=n$ à $2n$, on obtient la relation demandée :
$$0\leq\sum_{k=n}^{2n}f(k)\leq\sum_{k=n}^{2n}\dfrac{1}{k}-\dfrac{1}{k+1}=U_{n}$$
Comme $\lim_{n\mapsto +\infty}U_{n}=0$, le théorème des gendarmes permet de conclure que $$\lim_{n\mapsto +\infty}\sum_{k=n}^{2n}f(k)=0$$
d) La relation établie dans la question 1.b. donne par sommation :
$$\sum_{k=n}^{2n}\int_{k}^{k+1}\dfrac{\mathrm{d}x}{x}=\sum_{k=n}^{2n}\dfrac{1}{k}-\sum_{k=n}^{2n}f(k)$$
ou en faisant intervenir la relation de Schales pour les intégrales : $$\int_{n}^{2n+1}\dfrac{\mathrm{d}x}{x}=S_{n}-\sum_{k=n}^{2n}f(k)$$
Ensuite en intégrant : $\ln(k-1)-\ln k=S_{n}-\sum_{k=n}^{2n}f(k)$
Finalement $$\sum_{k=n}^{2n}f(k)=S_{n}-\ln\dfrac{2n+1}{n}$$
Puisque $\lim_{n\mapsto +\infty}\sum_{k=n}^{2n}f(k)=0$ et $\lim_{n\mapsto +\infty}\ln\dfrac{2n+1}{n}=\ln 2$, on en déduit que $$\lim_{n\mapsto +\infty}S_{n}=\ln 2$$
Exercice 3
a)
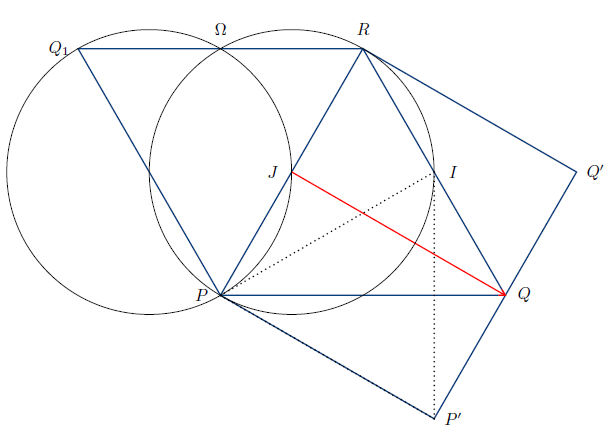
Le point $P'$ est tel que $f(P)=t\circ r(P)=t(P)=P'.$
Donc le point $P'$ est entièrement défini par la relation $\overrightarrow{PP}'=\overrightarrow{JQ}$;
$P'$ est tel que $JPP'Q$ soit un parallélogramme.
Le point $Q'$ est tel que $f(Q)=t\circ r(Q)=t(R)=Q'.$
Donc le point $Q'$ est entièrement défini par la relation $\overrightarrow{RQ}'=\overrightarrow{JQ}$;
$Q'$ est tel que $JQQ'R$ soit un parallélogramme.
b) La droite $(IJ)$ est une droite des milieux pour le triangle $PQR$, donc $JIR$ a même nature que $PQR$ :
$JIR$ est équilatéral direct
c) La droite $(JQ)$ est la médiatrice du segment $[PR]$ parce que le triangle $PQR$ est équilatéral.
Donc, puisque $J$ est le milieu de $[QQ_{1}]$, l'image $PQ_{1}R$ du triangle équilatéral direct $PQR$ par la symétrie orthogonale d'axe $(PR)$ est un triangle équilatéral indirect.
$r$ est la rotation de centre $P$ et d'angle $(\overrightarrow{PQ}\;,\ \overrightarrow{PR})=\dfrac{\pi}{3}.$ Donc $r(R)=Q_{1}.$
Ensuite, $f(R)=t\circ r(R)=t(Q_{1})=J\ \Rightarrow\ f(R)=J.$
On sait que $f=t\circ r$ est une rotation de même angle que $r$ c'est à dire $\dfrac{\pi}{3}.$
La relation $f(R)=J$ et $JIR$ est équilatéral direct entraîne que le centre de $f$ est $I.$
$f$ est la rotation de centre $I$ et d'angle $\dfrac{\pi}{3}.$
On en déduit, puisque $f(P)=P'$ que le triangle $IPP'$ est équilatéral direct .
2) $\begin{array}{|c|c|c|c|c|}\hline\text{Antécédent}&\Omega&J&R&I \\ \hline\text{Image par }s&\Omega&P&I&P'\\ \hline\end{array}$
a) L'angle de $s$ est $(\overrightarrow{JR}\;,\ \overrightarrow{PI})=(\overrightarrow{PJ}\;,\ \overrightarrow{PI}).$ L'angle de $s$ est $-\dfrac{\pi}{6}$
Le rapport de $s$ est $\dfrac{PI}{JR}.$ Or $PI=PR\cos\dfrac{\pi}{6}=2JR\dfrac{\sqrt{3}}{2}.$
Donc le rapport de $s$ est $\sqrt{3}.$
On a
\begin{eqnarray}(\overrightarrow{RI}\;,\ \overrightarrow{IP'}) &=& (\overrightarrow{IQ}\;,\ \overrightarrow{IP'}) \nonumber \\ &=& (\overrightarrow{IQ}\;,\ \overrightarrow{IP})+(\overrightarrow{IP}\;,\ \overrightarrow{IP'}) \nonumber \\ &=& -\dfrac{\pi}{2}+\dfrac{\pi}{3} \nonumber \\ &=& -\dfrac{\pi}{6}\quad\text{angle de }s \nonumber \end{eqnarray}
$\dfrac{IP'}{RI}=\dfrac{IP}{RI}=\sqrt{3}$ rapport de $s.$
Les trois conditions :
$\left\lbrace\begin{array}{rcl} s(R) &=& I \\ \\(\overrightarrow{RI}\;,\ \overrightarrow{IP'}) &=& \text{angle de }s \\ \\ \dfrac{IP'}{RI} &=& \text{rapport de }s \end{array}\right.\qquad\text{suffisent pour dire que }s(I)=P'$
b) Puisque les similitudes planes directes conservent les angles, on peut lire dans le tableau précédent que : angle de $s=(\overrightarrow{\Omega R}\;,\ \overrightarrow{\Omega I})=(\overrightarrow{JR}\;,\ \overrightarrow{PI}).$
Or $(\overrightarrow{JR}\;,\ \overrightarrow{PI})=(\overrightarrow{PR}\;,\ \overrightarrow{PI})$ parce que le point $J$ appartient au segment $[PR].$
Donc $(\overrightarrow{\Omega R}\;,\ \overrightarrow{\Omega I})=(\overrightarrow{PR}\;,\ \overrightarrow{PI})$ et comme les quatre points $\Omega\;,\ R\;,\ P$ et $I$ ne sont pas alignés, ils sont cocycliques.
De même $-\dfrac{\pi}{6}=\text{angle de }s=(\overrightarrow{\Omega J}\;,\ \overrightarrow{\Omega P}).$
D'un autre côté, la droite $(Q_{1}J)$ étant la bissectrice du triangle équilatéral indirect $PQ_{1}R$, l'angle $(\overrightarrow{Q_{1}J}\;,\ \overrightarrow{Q_{1}P})$ vaut $-\dfrac{\pi}{6}$
On en déduit que $(\overrightarrow{\Omega J}\;,\ \overrightarrow{\Omega P})=(\overrightarrow{Q_{1}J}\;,\ \overrightarrow{Q_{1}P})$ puis que les points $\Omega\;,\ J\;,\ P$ et $Q_{1}$ sont cocycliques
En résumé, le point $\Omega$ appartient à l'intersection des deux cercles $C_{1}$ et $C_{2}$ ; où $C_{1}$ est le cercle contenant les points $P\;,\ I$ et $R$ et $C_{2}$ le cercle contenant les points $P\;,\ J$ et $Q_{1}.$
De plus le point $\Omega$ est différent de $P$ parce que $\Omega$ est fixé par $s$ et $P$ non.
Ces conditions définissent parfaitement le point $\Omega.$
Problème
1) a) Nous sommes en présence d'une équation différentielle linéaire homogène à coefficients constants de degré un ou deux selon que $m$ est égal à 0 ou non.
L'équation caractéristique est : $$(E_{m}^{c})\ :\ mr^{2}+2r+2=0$$
$-$ Si $m=0\;,\ (E_{m}^{c})$ est une équation du premier degré. Sa seule racine est $r_{0}=-1.$
La solution générale de l'équation $(E_{m})$ est alors $y=k\mathrm{e}^{-t}\;,\ k$ constante réelle.
$-$ Si $m\neq 0\;,\ (E_{m}^{c})$ est une équation du second degré dont le discriminant réduit est $\Delta'=1-2m.$
$\ast$ Si $\Delta'$ est égal à 0 c'est à dire $m=\dfrac{1}{2}$, l'équation $(E_{m}^{c})$ a une racine double $r_{0}=-\dfrac{1}{m}=-2.$
La solution générale de l'équation $(E_{m})$ est alors $y=(at+b)\mathrm{e}^{-2t}\;,\ a$ et $b$ constantes réelles.
$\ast$ Si $\Delta'>0$ c'est à dire $m<\dfrac{1}{2}$, l'équation $(E_{m}^{c})$ a deux racines réelles simples
$$r_{1}=\dfrac{-1+\sqrt{1-2m}}{m}\quad\text{et}\quad r_{2}=\dfrac{-1-\sqrt{1-2m}}{m}$$
La solution générale de l'équation $(E_{m})$ est alors $y=a\mathrm{e}^{r_{1}t}+b\mathrm{e}^{r_{2}t}\;,\ a$ et $b$ constantes réelles.
$\ast$ Si $\Delta'<0$ c'est à dire $m>\dfrac{1}{2}$, l'équation $(E_{m}^{c})$ a deux racines complexes simples conjuguées
$$z_{1}=\dfrac{-1+\mathrm{i}\sqrt{2m-1}}{m}=\alpha+\mathrm{i}\beta\quad\text{et}\quad z_{2}=\dfrac{-1-\mathrm{i}\sqrt{2m-1}}{m}=\alpha-\mathrm{i}\beta$$
avec $\alpha=-\dfrac{1}{m}\ \text{ et }\ \beta=\dfrac{\sqrt{2m-1}}{m}$
La solution générale de l'équation $(E_{m})$ est alors $y=\mathrm{e}^{\alpha t}(a\cos\beta t+b\sin\beta t)\;,\ a$ et $b$ constantes réelles.
b) Notons $h$ la solution de $(E_{1})$ dont la courbe passe par le point $A$ et admet en ce point une tangente parallèle à la droite d'équation $y=-x.$
On doit alors avoir $h(0)=1$ et $h'(0)=-1.$
Ici $m=1$ est > à $\dfrac{1}{2}$, donc $h$ s'écrit : $h(t)=\mathrm{e}^{-t}(a\cos t+b\sin t)\;,\ a$ et $b$ constantes réelles.
$h'(t)=[(b-a)\cos t-(b+a)\sin t]\mathrm{e}^{-t}$
Les conditions satisfaites par h deviennent : $h(0)=a=1$ et $h'(0)=b-a=-1$ c'est à dire $a=1$ et $b=0$ puis $h(t)=\cos t\mathrm{e}^{-t}$
2) La fonction $f$ est continue et dérivable dans $I=\left[-\dfrac{\pi}{2}\;,\ \dfrac{3\pi}{2}\right]$ et $\forall\;t\in\;I\;,\ f'(t)=-(\cos t-\sin t)\mathrm{e}^{-t}$ (déjà calculé dans la question précédente).
L'équation $\cos t+\sin t=0$ est équivalente à $\cos\left(t-\dfrac{\pi}{4}\right)=0.$ Ses solutions dans $\mathbb{R}$ sont telles que
$$t-\dfrac{\pi}{4}=\dfrac{\pi}{2}+k\pi\;,\ k\in\mathbb{Z}\quad\text{soit}\ t=\dfrac{3\pi}{4}+k\pi\;,\ k\in\mathbb{Z}$$
Les solutions de cette équation dans $I$ sont alors $t_{0}=\dfrac{3\pi}{4}$ et $t_{1}=-\dfrac{\pi}{4}.$
Cette équation et la dérivée $f'$ ont les mêmes zéro.
Pour déterminer le signe de $f'$ on peut résoudre des inéquations trigonométriques.
Mais on peut aussi dire que dans tout intervalle où $f'$ ne s'annule pas, elle garde un signe constant parce qu'elle est continue. C'est une application très pratique du théorème des valeurs intermédiaires.
$-\dfrac{\pi}{3}$ appartient à l'intervalle $I_{1}=\left[-\dfrac{\pi}{2}\;,\ -\dfrac{\pi}{4}\right]$ et $f'\left(-\dfrac{\pi}{3}\right)=\left(\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}\right)\mathrm{e}^{\tfrac{\pi}{3}}$ est > 0, donc $f'$ est > 0 dans $I_{1}.$
0 appartient à l'intervalle $I_{2}=\left[-\dfrac{\pi}{4}\;,\ \dfrac{3\pi}{4}\right]$ et $f'(0)=-1$ est < 0, donc $f'$ est < 0 dans $I_{2}.$
$\pi$ appartient à l'intervalle $I_{3}=\left[\dfrac{3\pi}{4}\;,\ \dfrac{3\pi}{2}\right]$ et $f'(\pi)=\mathrm{e}^{-\pi}$ est > 0, donc $f'$ est > 0 dans $I_{3}.$
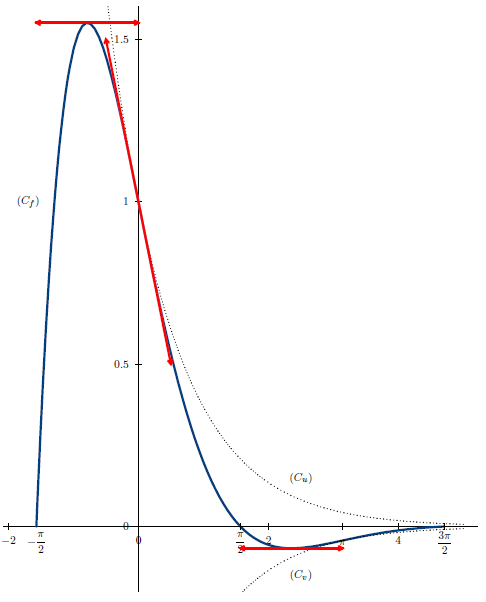
Voici le tableau de variations de $f.$
$$\begin{array}{|c|lcccccr|}\hline t&-\frac{\pi}{2}& &-\frac{\pi}{4}& &\frac{3\pi}{4}& &\frac{3\pi}{2} \\ \hline f'& &+&|&-&|&+& \\ \hline & & &r& & & &0 \\ f& &\nearrow& &\searrow& &\nearrow& \\ &0& & & &s& & \\ \hline\end{array}$$
$$s=-\tfrac{\sqrt{2}}{2}\mathrm{e}^{-\tfrac{3\pi}{4}}\;,\quad r=\tfrac{\sqrt{2}}{2}\mathrm{e}^{\tfrac{\pi}{4}}$$
Et voici les courbes représentatives de $f\;,\ u$ et $v.$
3) a) Pour tout $k$ appartenant à $\mathbb{Z}$ et tout $t$ appartenant à $\mathbb{R}\;,\ g(t+2k\pi)=\mathrm{e}^{-t-2k\pi}\cos t$ parce que la fonction cosinus est périodique de période $2\pi.$
Donc $g(t+2k\pi)=\mathrm{e}^{-2k\pi}g(t).$
En dérivant cette dernière expression par rapport à t on obtient : $g'(t+2k\pi)=\mathrm{e}^{-2k\pi}g'(t).$
En particulier pour tout $t$ appartenant à $I$ et tout $k$ appartenant à $\mathbb{Z}\;,\ g'(t+2k\pi)=\mathrm{e}^{-2k\pi}f'(t).$
Cette relation permet de déterminer parfaitement le signe de $g'$ dans $\mathbb{R}.$
Plus précisément :
Si $t$ appartient à un intervalle du genre $$\left[-\dfrac{\pi}{2}+2k\pi\;,\ -\dfrac{\pi}{4}+2k\pi\right]\ \text{ ou }\ \left[\dfrac{3\pi}{4}+2k\pi\;,\ \dfrac{3\pi}{2}+2k\pi\right]\;,\ k\in\mathbb{Z}$$ alors $g'(t)$ est positif
Si $t$ appartient à un intervalle du genre $$\left[-\dfrac{\pi}{4}+2k\pi\;,\ \dfrac{3\pi}{4}+2k\pi\right]\;,\ k\in\mathbb{Z}$$ alors $g'(t)$ est positif
b) Un point $M$ de coordonnées $(t\;,\ u(t))$ appartient à $\Gamma\cap C_{u}$ si et seulement si $u(t)=g(t)$ c'est
à dire $\cos t=1$ ou $t=2k\pi\;,\ k$ appartenant à $\mathbb{Z}$, et alors $u(t)=\mathrm{e}^{-2k\pi}.$
Donc $\Gamma\cap C_{u}=\{M(2k\pi\;,\ \mathrm{e}^{-2k\pi})\;,\ k\in\mathbb{Z}\}$
Un point $M$ de coordonnées $(t\;,\ v(t))$ appartient à $\Gamma\cap C_{v}$ si et seulement si $v(t)=g(t)$ c'est
à dire $\cos t=-1$ ou $t=(2k+1)\pi\;,\ k$ appartenant à $\mathbb{Z}$, et alors $v(t)=\mathrm{e}^{-(2k+1)\pi}.$
Donc $\Gamma\cap C_{v}=\{M((2k+1)\pi\;,\ \mathrm{e}^{-(2k+1)\pi})\;,\ k\in\mathbb{Z}\}$
c) En un point $M(2k\pi\;,\ \mathrm{e}^{-2k\pi})$ commun à $\Gamma$ et à $C_{u}$, la pente de la tangente à $\Gamma$ est
\begin{eqnarray} g'(2k\pi) &=& \mathrm{e}^{-2k\pi}g'(0) \nonumber \\ &=& \mathrm{e}^{-2k\pi}f'(0) \nonumber \\ &=& -\mathrm{e}^{-2k\pi} \nonumber \end{eqnarray}
et la pente de la tangente à $C_{u}$ est
\begin{eqnarray} u'(2k\pi) &=& -\mathrm{e}^{-t}|_{t=2k\pi} \nonumber \\ &=& -\mathrm{e}^{-2k\pi} \nonumber \end{eqnarray}
Les deux tangentes ayant même pente et passant par le point $M$ sont confondues.
En un point $M((2k+1)\pi\;,\ \mathrm{e}^{-(2k+1)\pi})$ commun à $\Gamma$ et à $C_{v}$, la pente de la tangente à $\Gamma$ est
\begin{eqnarray} g'((2k+1)\pi) &=& \mathrm{e}^{-2k\pi}g'(\pi) \nonumber \\ &=& \mathrm{e}^{-2k\pi}f'(\pi) \nonumber \\ &=& -\mathrm{e}^{-(2k+1)\pi} \nonumber \end{eqnarray}
et la pente de la tangente à $C_{v}$ est
\begin{eqnarray} v'((2k+1)\pi) &=& -\mathrm{e}^{-t}|_{t=(2k+1)\pi} \nonumber \\ &=& -\mathrm{e}^{-(2k+1)\pi} \nonumber \end{eqnarray}
Les deux tangentes ayant même pente et passant par le point $M$ sont confondues.
d) $0\leq|\cos t\mathrm{e}^{-t}|\leq\mathrm{e}^{-t}.$ Or $\lim_{t\rightarrow +\infty}\mathrm{e}^{-t}=0$
Le théorème des gendarmes permet de conclure que $\lim_{t\rightarrow +\infty}g(t)=0.$
4) a) Pour simplifier posons $r_{k}=-\dfrac{\pi}{2}+k\pi\;,\ s_{k}=\dfrac{\pi}{2}+k\pi$ de sorte que $$a_{k}=\int_{r_{k}}^{s_{k}}g_{k}(t)\mathrm{d}t$$
ensuite intégrons une première fois par parties en posant :
$\left\lbrace\begin{array}{rclcrcl} u(t) &=& \mathrm{e}^{-t} &\Rightarrow& u'(t) &=& -\mathrm{e}^{-t} \\ v'(t) &=& \cos t &\Leftarrow& v(t) &=& \sin t \end{array}\right.$
Alors $a_{k}=\left[\sin t\mathrm{e}^{-t}\right]_{r_{k}}^{s_{k}}+\int_{r_{k}}^{s_{k}}\sin t\mathrm{e}^{-t}\mathrm{d}t$
intégrons une deuxième fois par parties en posant :
$\left\lbrace\begin{array}{rclcrcl} u(t) &=& \mathrm{e}^{-t} &\Rightarrow& u'(t) &=& -\mathrm{e}^{-t} \\ v'(t) &=& \sin t &\Leftarrow& v(t) &=& -\cos t \end{array}\right.$
Alors $a_{k}=\left[\sin t\mathrm{e}^{-t}\right]_{r_{k}}^{s_{k}}+\left[-\cos t\mathrm{e}^{-t}\right]_{r_{k}}^{s_{k}}-\int_{r_{k}}^{s_{k}}\cos t\mathrm{e}^{-t}\mathrm{d}t$
c'est à dire $a_{k}=\left[(\sin t-\cos t)\mathrm{e}^{-t}\right]_{r_{k}}^{s_{k}}-a_{k}$ ou $a_{k}=\dfrac{1}{2}\left[(\sin t-\cos t)\mathrm{e}^{-t}\right]_{r_{k}}^{s_{k}}$
Or $\cos r_{k}=\cos s_{k}=0$ et $\sin r_{k}=(-1)^{k+1}$ et $\sin s_{k}=(-1)^{k}$
Donc
\begin{eqnarray} a_{k} &=& \dfrac{1}{2}(-1)^{k}[\mathrm{e}^{-s_{k}}-(-1)^{k+1}\mathrm{e}^{-r_{k}}] \nonumber \\ &=& \dfrac{1}{2}(-1)^{k}[\mathrm{e}^{-s_{k}}+\mathrm{e}^{-r_{k}}] \nonumber \\ &=& \dfrac{1}{2}(-1)^{k}\mathrm{e}^{-k\pi}[\mathrm{e}^{-\frac{\pi}{2}}+\mathrm{e}^{\frac{\pi}{2}}] \nonumber \end{eqnarray}
b) $s_{n}=C_{h}\sum_{k=0}^{n}\mathrm{e}^{-k\pi}$ avec $C_{h}=\dfrac{1}{2}[\mathrm{e}^{-\frac{\pi}{2}}+\mathrm{e}^{\frac{\pi}{2}}]$
La somme est la somme des $n+1$ premiers termes de la progression géométrique de premier terme 1 et de raison $\mathrm{e}^{-\pi}$
Donc $s_{n}=C_{h}.1.\dfrac{1-\mathrm{e}^{-(n+1)\pi}}{1-\mathrm{e}^{-\pi}}$
Puisque $\lim_{n\mapsto +\infty}\mathrm{e}^{-(n+1)\pi}=0$, la suite $(s_{n})$ admet une limite et cette limite est égale à : $$s=\lim_{n\mapsto +\infty}s_{n}=C_{h}\dfrac{1}{1-\mathrm{e}^{-\pi}}$$
$s_{n}$ représente l'aire géométrique du domaine plan délimité par l'axe des abscisses, la verticale d'équation $x=-\dfrac{\pi}{2}$, la verticale d'équation $x=\dfrac{\pi}{2}+n\pi$ et la courbe représentative de $g.$
$s$ représente l'aire géométrique du domaine plan délimité par l'axe des abscisses, la verticale d'équation $x=-\dfrac{\pi}{2}$ et la courbe représentative de $g.$
5) a) $x'_{t}=-(\cos t+\sin t)\mathrm{e}^{-t}$ et $y'_{t}=(\cos t-\sin t)\mathrm{e}^{-t}$
On a :
\begin{eqnarray} x'_{t} &=& -(\cos t+\sin t)\mathrm{e}^{-t} \nonumber \\ &=& -\cos\left(t-\dfrac{\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t} \nonumber \\ &=& \cos\left(\pi+t-\dfrac{\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t} \nonumber \\ &=& \cos\left(t+\dfrac{3\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t} \nonumber \end{eqnarray}
et
\begin{eqnarray} y'_{t} &=& (\cos t-\sin t)\mathrm{e}^{-t}\nonumber \\ &=& -\sin\left(t-\dfrac{\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t} \nonumber \\ &=& \sin\left(\pi+t-\dfrac{\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t} \nonumber \\ &=& \sin\left(t+\dfrac{3\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t} \nonumber \end{eqnarray}
Les zéro de $x'$ sont $t_{1}=-\dfrac{\pi}{4}$ et $t_{2}=\dfrac{3\pi}{4}$
Le zéro de $y'$ est $t_{3}=\dfrac{\pi}{4}$
On détermine les signes de $x'$ et $y'$ par la méthode utilisée pour déterminer le signe de $f'.$
Voici le tableau de variations conjointes.
$$\begin{array}{|c|lcccccccr|}\hline t&-\frac{\pi}{2}& &-\frac{\pi}{4}& &\frac{\pi}{4}& &\frac{3\pi}{4}& &\frac{3\pi}{2} \\ \hline x'& &+&|&-&|&-&|&+& \\ \hline & & &r& &|& &|& &0 \\ x& &\nearrow&|&\searrow&s&\searrow&|&\nearrow& \\ &0& &|& &|& &t& & \\ \hline & & &|& &s& &|& & \\ y& &\nearrow&-r&\nearrow&|&\searrow&-t&\searrow& \\ &v& &|& &|& &|& &u \\ \hline y'& &+&|&+&|&-&|&-& \\ \hline\end{array}$$
$r=\dfrac{\sqrt{2}}{2}\mathrm{e}^{\tfrac{\pi}{4}}\;,\quad s=\dfrac{\sqrt{2}}{2}\mathrm{e}^{-\tfrac{\pi}{4}}\;,\quad t=-\dfrac{\sqrt{2}}{2}\mathrm{e}^{-\tfrac{3\pi}{4}}\;,\quad u=-\mathrm{e}^{-\tfrac{3\pi}{2}}\;,\quad v=-\mathrm{e}^{\tfrac{\pi}{2}}$
Voici la courbe $(\Lambda)$
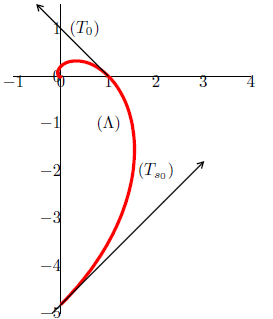
La tangente $(T_{s_{0}})$ au point de paramètre $s_{0}=-\dfrac{\pi}{2}$ est la droite passant par le point de coordonnées $(0\;,\ -\mathrm{e}^{-s_{0}})$ et dont un vecteur directeur a pour coordonnées $(x'_{s_{0}}\;,\ y'_{s_{0}})=(\mathrm{e}^{-s_{0}}\;,\ \mathrm{e}^{-s_{0}})$ ou $(1\;,\ 1).$
La tangente $(T_{0})$ au point de paramètre 0 est la droite passant par le point de coordonnées $(1\;,\ 0)$
et dont un vecteur directeur a pour coordonnées $(x'_{s_{0}}\;,\ y'_{s_{0}})=(-1\;,\ 1).$
b) Rappelons que $\theta$ étant un réel, le plan étant muni d'un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j})$ et en désignant par $M_{\theta}$ le point de cordonnées $(\lambda\cos\theta\;,\ \lambda\sin\theta)\;,\ \lambda>0$ alors $\theta$ est une mesure de l'angle $(\vec{i}\;,\ \overrightarrow{OM_{\theta}}).$
On en déduit que $(\vec{i}\;,\ \overrightarrow{OM_{t}})\equiv t$
$\vec{V}_{t}$ a pour coordonnées $x'_{t}=\cos\left(t+\dfrac{3\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t}$ et $y'_{t}=\sin\left(t+\dfrac{3\pi}{4}\right)\sqrt{2}\mathrm{e}^{-t}$
Donc $(\vec{i}\;,\ \vec{V}_{t})\equiv t+\dfrac{3\pi}{4}.$
Puis $(\overrightarrow{OM_{t}}\;,\ \vec{V}_{t})=(\overrightarrow{OM_{t}}\;,\ \vec{i})+(\vec{i}\;,\ \vec{V}_{t})\equiv \dfrac{3\pi}{4}.$
Auteur: Mouhamadou Ka

Ajouter un commentaire