Vous êtes ici

Bac Physique Chimie 1er Groupe S1 S3 2018

Exercice 1 (03 points)

Une acidité très élevée affaiblit les systèmes d'auto-défense de notre corps.

Pour lutter contre la surproduction d'acide chlorhydrique par le suc gastrique qui peut provoquer des remontées acides ou brûlures d'estomac, on peut utiliser des antiacides.

Ces derniers sont des bases qui permettent de neutraliser le surplus d'acide.

1.1 Utilisation d'une solution d'hydroxyde de sodium.

Un groupe d'élèves prépare une solution

$S_{S}$ d'hydroxyde de sodium de concentration molaire

$C_{S}$ afin de l'utiliser comme antiacide.

Pour neutraliser

$500\;mL$ d'une solution d'acide chlorhydrique de même

$pH$ que le suc gastrique que l'on prendra égal à

$2$ , il a fallu que le groupe ajoute

$50\;mL$ de la solution

$S_{S}$

1.1.1 Montrer que la concentration molaire

$C_{S}$ de la solution

$S_{S}$ d'hydroxyde de sodium vaut

$0.1\;mol\cdot L^{-1}.$

$(0.5\;pt)$

1.1.2 Les

$50\;mL$ de la solution

$S_{S}$ d'hydroxyde de sodium ont été préparés à partir d'une solution commerciale

$S_{0}$ d'hydroxyde de sodium dont l'étiquette porte les indications suivantes :

hydroxyde de sodium ; densité

$1.25$ ; pourcentage massique

$8\%$ ; masse molaire

$40\;g\cdot mol^{-1}.$

1.1.2.1 Calculer la concentration molaire

$C_{0}$ de la solution commerciale

$S_{0}.$

$(0.5\;pt)$

1.1.2.2 Décrire la préparation de la solution

$S_{S}$ à partir de la solution commerciale

$S_{0}$ en indiquant le volume

$V_{0}$ à prélever et le matériel à utiliser.

$(0.5\;pt)$

1.2 Utilisation d'une solution de benzoate de sodium.

Le benzoate de sodium est retrouvé dans de nombreux produits alimentaires comme conservateur.

Un autre groupe d'élèves choisissent de l'utiliser comme antiacide.

Ces élèves dissolvent une masse

$m=72\;mg$ de benzoate de sodium

$C_{6}H_{5}COONa$ dans

$100\;mL$ d'eau pour obtenir une solution notée

$S_{B}.$

1.2.1 Écrire l'équation-bilan de la réaction entre une solution de benzoate de sodium et une solution d'acide chlorhydrique.

Calculer la constante de réaction.

$(0.5\;pt)$

1.2.2 L'utilisation comme antiacide du benzoate de sodium par les élèves est-elle justifiée ? pourquoi ?

$(0.25\;pt)$

1.2.3 Le groupe d'élèves ajoute un volume

$V_{A}$ d'une solution

$S_{A}$ d'acide chlorhydrique de concentration molaire

$C_{A}=0.01\;mol\cdot L^{-1}$ à la solution

$S_{B}$ précédente.

Il obtient une solution

$S$ dans laquelle les concentrations molaires en acide benzoïque et en ion benzoate sont égales.

1.2.3.1 Calculer le volume

$V_{A}.$

$(0.25\;pt)$

1.2.3.2 Quel est le

$pH$ de la solution

$S$ ?

justifier la réponse.

Donner les propriétés de la solution

$S.$

$(0.5\;pt)$

Données :

Masses molaires en

$g\cdot mol^{-1}$ :

$M(C)=12$ ;

$M(H)=1$ ;

$M(O)=16$ ;

$M(Na)=23.$

$pKa(C_{6}H_{5}COOH/C_{6}H_{5}COO^{-})=4.2$ ;

$pKa(H_{3}O^{+}/H_{2}O)=0$ et

$pKa(H_{2}O/OH^{-})=14.$

Exercice 2 (03 points)

La glutaminylalanine, dipeptide formé à partir de la glutamine et de l'alanine, est un produit de dégradation incomplète de la digestion des protéines.

Il est connu pour avoir des effets physiologiques.

2.1 La molécule du dipeptide.

La molécule de la glutaminylalanine est représentée par la formule semi-développée ci-dessous :

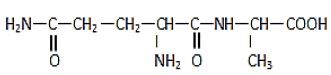
2.1.1. Recopier la formule.

Encadrer les groupes fonctionnels et les nommer.

$(0.5\;pt)$

2.1.2. Indiquer la liaison peptidique.

$(0.25\;pt)$

2.1.3 Repérer par un astérisque

$(\ast)$ les atomes de carbone asymétriques dans la molécule.

$(0.25\;pt)$

2.2. Étude de l'acide

$\alpha-aminé\ N-terminal\ du\ dipeptide$

La glutamine, l'acide

$\alpha$ -aminé

$N$ -terminal du dipeptide, est l'acide aminé le plus abondant dans le sang et dans les muscles.

Le corps est capable de synthétiser lui-même la

$L$ -glutamine que l'on retrouve aussi dans la viande, le poisson, les produits laitiers, les céréales et les légumineuses.

Parmi les rôles de la

$L$ -glutamine, on peut citer l'amélioration des performances physiques, la réduction de la sensation de la fatigue chez les joueurs de football...

2.2.1. Définir un acide

$\alpha$ -aminé.

$(0.25\;pt)$

2.2.2. Montrer que la molécule de glutamine est chirale.

$(0.25\;pt)$

2.2.3. Donner la représentation de Fisher de la

$L$ -glutamine

$(0.25\;pt)$

2.3 Étude de l'acide

$\alpha$ -aminé

$C$ -terminal du dipeptide

L'alanine, l'acide

$\alpha$ -aminé

$C$ -terminal de la glutaminylalanine, est aussi un acide aminé qui se retrouve dans les mêmes sources alimentaires que la glutamine.

Elle fait augmenter le taux de sucre dans le sang et contribue à la formation des globules blancs, elle est donc indispensable au maintien d'une bonne santé.

2.3.1. En solution aqueuse la molécule d'alanine se présente sous forme d'un ion dipolaire entre autres espèces chimiques.

Donner la formule et le nom de cet ion.

$(0.5\;pt)$

2.3.2. Écrire l'équation-bilan de la réaction de l'ion dipolaire en milieu très acide puis en milieu très basique.

Quels sont les couples acide-base auxquels participe l'ion dipolaire ?

$(0.5\;pt)$

2.3.3 Les

$pKa$ des couples précédents valent

$2.3$ et

$9.9.$

Proposer un diagramme de prédominance des espèces d'une solution aqueuse d'alanine.

$(0.25\;pt)$

Exercice 3 (04 points)

La viscosité d'un liquide caractérise à la fois la force de résistance qu'il exerce sur un objet en chute et sa résistance à l'écoulement.

Avec un dispositif approprié, il est possible de suivre l'évolution du mouvement de chute d'une bille dans un tube vertical contenant le liquide à étudier et de déduire la viscosité dudit liquide à partir de la vitesse limite de chute.

Une bille sphérique homogène

$S$ , de masse

$m$ et de rayon

$r$ , pénètre verticalement dans un bassin de stockage supposé infiniment profond, rempli d'un liquide de masse volumique

$\mu$ (figure 1).

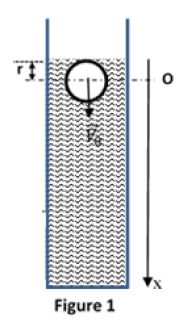
Le centre de la bille arrive à l'instant

$t=0$ en

$O$ , à la distance

$r$ de la surface libre du liquide à l'intérieur du bassin, avec une vitesse verticale de plongée

$\overrightarrow{V_{0}}.$

L'étude du mouvement se fera suivant l'axe

$Ox$ vertical dirigé vers le bas.

La bille est soumise à trois forces :

- le poids

$\overrightarrow{P}$ ;

-la force de viscosité

$\overrightarrow{f}$ opposée au déplacement, proportionnelle à la vitesse et supposée appliquée au centre d'inertie

$G$ de la bille :

$\overrightarrow{f}=-k\overrightarrow{V}$ , relation où

$k$ est une constante positive liée à la viscosité du liquide ;

-la poussée d'Archimède

$\overrightarrow{F}=-\mu\times\dfrac{4\pi r^{3}}{3}\times\overrightarrow{g}.$

3.1. Représenter, à un instant

$t$ donné, la bille et les forces extérieures appliquées au centre d'inertie.

$(0.5\;pt)$

3.2. En appliquant le théorème du centre d'inertie, montrer que l'équation différentielle du mouvement relative à la vitesse

$V=ẋ$ du centre d'inertie de la bille s'écrit :

$\dfrac{\mathrm{d}V}{\mathrm{d}t}+\dfrac{k}{m}V=\left(1-\dfrac{4\pi\mu r^{3}}{3m}\right)g$

$(0.75\;pt)$

3.3. Montrer que la vitesse du centre d'inertie atteint une limite

$V_{L}$ dont on donnera l'expression en fonction de

$k$ ,

$m$ ,

$\mu$ ,

$r$ et

$g.$

Sachant que

$V_{L}=24\;m\cdot s^{-1}$ en déduire la valeur de

$k.$

$(0.75\;pt)$

3.4. La solution générale de l'équation différentielle précédente est de la forme :

$V=A+B\mathrm{e^{-\dfrac{kt}{m}}}$ , relation où

$A$ et

$B$ sont des constantes.

Établir les expressions de

$A$ et

$B$ respectivement en fonction de

$V_{L}$ et de

$V_{0}$ et

$V_{L}$ en se plaçant aux conditions limites

$(t=0$ et

$t\rightarrow \infty).$

Donner alors l'expression de la vitesse instantanée

$V$ du centre d'inertie de la bille en fonction de

$V_{0}\;,\ V_{L}\;,\ k\;,\ m$ et le temps

$t$

$(0.75\;pt)$

3.5. Déterminer la loi horaire

$x(t)$ du mouvement vertical du centre d'inertie de la bille dans le liquide en fonction de

$V_{0}\;,\ V_{L}\;,\ k\;,\ m$ et le temps

$t.$

$(0.75\;pt)$

3.6. Évaluer, à l'issue de

$10\;s$ de chute, le bilan des travaux des forces appliquées à la bille.

En déduire le travail de la force de viscosité pour cette durée.

$(0.5 pt)$

On donne :

$m=1.4\;kg$ ;

$r=3.5\;cm$ ;

$\mu=860\;kg\cdot m^{-3}$ ;

$V_{0}=2\;m/s$ ;

$g=9.8\;m\cdot s^{-2}.$

Exercice 4 (05.5 points)

Pour étudier la charge et la décharge d'un condensateur on réalise le circuit de la figure 2 représentée ci-dessous.

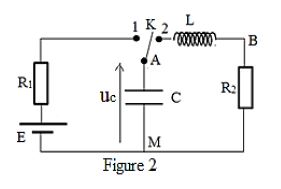
Données :

$E=4V$ ;

$R_{1}=1k\Omega$ ;

$R_{2}=400\Omega$ ;

$C=1\mu F$ ;

$L=0.4H.$

La résistance du générateur et celle de la bobine sont supposées négligeables.

4.1 Étude de la charge du condensateur

Le condensateur étant initialement déchargé, on ferme l'interrupteur

$K$ en position

$1$ à l'instant

$t=0.$

On note par

$u_{c}(t)$ la tension aux bornes du condensateur et

$i(t)$ l'intensité du courant dans le circuit.

4.1.1 Établir l'équation reliant les tensions instantanées aux bornes des trois composants du circuit.

En déduire l'équation différentielle relative à la tension

$u_{c}(t)$ aux bornes du condensateur.

$(0.5\;pt)$

4.1.2 Vérifier que l'expression

$u_{c}(t)=E\left(1-\mathrm{e^{-\dfrac{t}{\tau}}}\right)$ avec

$\tau=R_{1}C$ est solution de l'équation différentielle établie à la question précédente.

Donner la signification de

$\tau$ et calculer sa valeur.

$(0.5\;pt)$

4.1.3 Déterminer l'expression de l'intensité du courant

$I_{0}$ à

$t=0$ ; faire l'application numérique.

$(0.5\;pt)$

4.1.4 Déterminer les expressions, à l'instant

$t$ , de la puissance fournie par le générateur et de la puissance reçue par le condensateur en fonction de

$E\;,\ R_{1}\;,\ t et .$

$(0.5\;pt)$

4.1.5 Montrer que le rapport de l'énergie emmagasinée par le condensateur

$\epsilon(c)$ sur l'énergie fournie par le générateur

$\epsilon(G)$ entre l'instant de fermeture du circuit et une date quelconque

$t=x$ (

$x$ est un nombre positif) est donné par :

$\dfrac{\epsilon(c)}{\epsilon(G)}=\dfrac{1-\mathrm{e^{-x}}}{2}$

$(0.5\;pt)$

4.1.6 Pour différentes dates

$t=x$ où

$x$ est donné dans le tableau ci-dessous, reproduire le tableau sur la feuille de copie et le compléter.

$(0.5\;pt)$

$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x&0&0.01&0.10&1&5&10&100&+\infty\\ \hline \mathrm{e^{-x}}& & & & & & & & \\ \hline \dfrac{\epsilon(c)}{\epsilon(G)}& & & & & & & &\\ \hline \end{array}$

4.1.7 En exploitant le tableau, montrer que l'énergie fournie par le générateur n'est pas totalement reçue par le condensateur.

Expliquer pourquoi.

$(0.25\;pt)$

4.1.8 En se servant du tableau, déterminer la quantité de chaleur totale dégagée par effet joule au cours de la charge du condensateur.

$(0.25\;pt)$

4.2 Étude de la décharge.

A la fin de la charge du condensateur, on bascule l'interrupteur

$K$ de la position

$1$ à la position

$2.$

Cet instant est choisi comme nouvelle origine des dates

$t=0.$

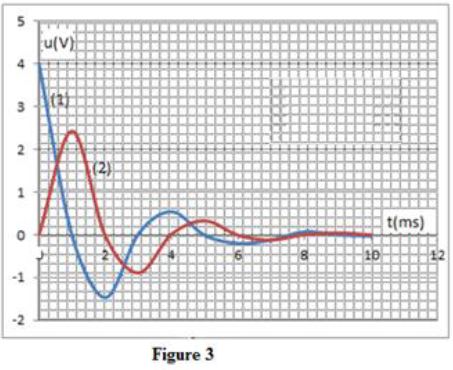
Les courbes

$(1)$ et

$(2)$ de la figure

$3$ représentent dans un ordre quelconque la tension

$u_{AM}$ aux bornes du conducteur ohmique de résistance

$R_{2}$ et la tension

$u_{AM}$ aux bornes du condensateur.

4.2.1 Recopier la figure

$2$ et y indiquer les branchements pour visualiser les tensions

$u_{AM}$ à la voie

$1$ et

$u_{BM}$ à la voie

$2$ d'un oscilloscope.

$(0.5\;pt)$

4.2.2 Affecter à chaque courbe la tension correspondante.

Justifier.

$(0.5\;pt)$

4.2.3 Expliquer l'allure des courbes.

Quelle est la courbe qui montre les variations de l'intensité du courant ?

Justifier.

$(0.5\;pt)$

4.2.4 En exploitant la figure

$3$ , déterminer l'énergie restante dans le circuit à la date

$t=2\;ms.$

La comparer avec l'énergie du condensateur à

$t=0.$

$(0.5\;pt)$

Exercice 5 (04.5 points)

La radiothérapie est utilisée dans certains cas pour le traitement de tumeurs.

Le rayonnement utilisé dans ces machines est constitué de particules légères béta moins

$(\beta^{-})$ émise par une source de cobalt-

$60$

$\left(^{60}Co\right).$

Dans certains cas, il est nécessaire d'utiliser un rayonnement

$\alpha\left(^{4}_{2}He\right)$ plus ionisant.

Le cobalt-

$60$ est un élément radioactif obtenu à partir du cobalt-

$59$

$\left(^{59}Co\right)$ bombardé par un flux de neutrons.

Le cobalt-

$60$ a une constante radioactive

$\gamma=3.60\cdot 10^{-4}\;jour^{-1}.$

Un condensateur de capacité

$C=100\mu F$ , initialement déchargé, est installé à la sortie du rayonnement émis par une source de cobalt-

$60$ à une date prise comme origine des temps

$t=0.$

Un dispositif adéquat permet d'assurer que l'essentiel des particules émises arrivent sur l'armature

$A$ du condensateur en face de la source (figure 4).

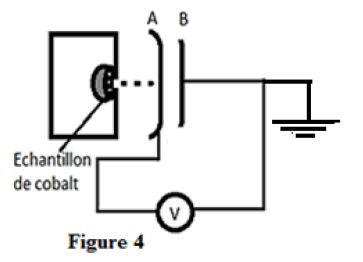
L'armature

$B$ est reliée à la terre.

Un voltmètre indique à chaque instant la tension

$U_{BA}$ aux bornes du condensateur.

5.1 Donner la différence entre une réaction nucléaire naturelle et une réaction nucléaire artificielle.

$(0.5\;pt)$

5.2 Écrire les équations des réactions nucléaires du cobalt citées dans le texte.

$(0.5\;pt)$

5.3 En considérant la réaction spontanée du cobalt, calculer en

$MeV$ et en joule l'énergie libérée lors de cette désintégration.

$(0.5\;pt)$

5.4 En déduire l'énergie libérée par désintégration de

$1\;mg$ de cobalt-

$60.$

$(0.75\;pt)$

5.5 Au bout de quatre

$(04)$ heures, le voltmètre branché aux bornes du condensateur indique une tension

$U_{BA}=10V.$

Exprimer puis calculer :

5.5.1 la charge

$\mathbb{Q}$ portée par l'armature

$A$ du condensateur.

$(0.5\;pt)$

5.5.2 la variation

$\Delta N$ du nombre de noyau de cobalt-

$60.$

$(0.75\;pt)$

5.5.3 l'activité initiale

$A_{0}$ de l'échantillon de cobalt-

$60.$

$(0.5\;pt)$

5.5.4 la masse initiale de cet échantillon de cobalt.

$(0.5\;pt)$

Données :

Charge élémentaire :

$e=1.6\cdot10^{-19}C$ ; masse molaire atomique du cobalt

$60$ :

$M=59.93\;g\cdot mol^{-1}$ ; Nombre d'Avogadro :

$\mathcal{N}=6.02\cdot 10^{23} mol^{-1}$ ; masse de l'électron :

$m=9.11\cdot10^{-31} kg.$

Masse en unité de masse atomique :

$m(^{60}Co)=59.95654 u$ ;

$m(^{60}Ni)=59.95351 u$ ;

$m(^{60}Fe)=55.95614 u$ ; Unité de masse atomique :

$1u=1.6605\cdot10^{-27} kg=931.5\dfrac{M_{e}V}{C^{2}}.$

Vitesse de la lumière dans le vide :

$C=3\cdot10^{8} m\cdot s^{-1}$

Extrait du tableau de classification

$\begin{array}{|c|c|c|c|c|} \hline _{25}Mn&_{26}Fe&_{27}Co&_{28}Ni&_{29}Cu\\ \hline \end{array}$

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Bac Physique Chimie 1er Groupe S1 S3 2018

Formulaire de recherche

Exercice 1 (03 points)

Exercice 2 (03 points)

Exercice 3 (04 points)

Exercice 4 (05.5 points)

Exercice 5 (04.5 points)

Ajouter un commentaire

Plain text