Bac Physique chimie 1er groupe S1, S1A, S3 2021
Exercice 1
On donne en $g/mol$ $M(C)=12$ ; $M(H)=1$ et $M(0)=16$
Les acides carboxyliques présentent une grande importance industrielle pour la fabrication de solvants, de shampoings, de peintures, de bougie, de textiles et d'antiseptiques.
Les acides carboxyliques peuvent être obtenus par oxydation des aldéhydes ou des alcools.
Les acides gras peuvent s'obtenir par saponification des graisses animales ou végétales.
On considère un monoalcool aliphatique saturé à chaîne carbonée ramifiée de masse molaire $M=88g\cdot mol^{-1}.$
1.1 Déterminer la formule brute de cet alcool.
1.2 Donner la formule semi développée et le nom de chacun des alcools isomères à chaîne ramifiée présentant un carbone asymétrique.
1.3 On considère maintenant deux alcools $A$ et $B$ : $A$ est le $2-$méthylbutan$-1-$ol et $B$ est le $3-$méthylbutan $-1-$ol.
$A$ est oxydé par une solution de dichromate de potassium $K_{2}Cr_{2}O_{7}.$
Il donne $A'$ qui réagit avec la $DNPH$ et le réactif de Tollens.
1.3.1 Écrire l'équation bilan de la réaction entre $A$ et les ions dichromates.
On donne $Cr_{2}O_{7}^{2-}|Cr^{3+}$ ; $A'|A$
1.3.2 l'alcool $(B)$ réagit avec un acide carboxylique $(C)$, pour donner l'éthanoate de $3-$methylbutyle $(E).$
1.3.2.1 Donner la formule semi développée de $(C).$
Écrire l'équation bilan de la réaction.
Donner les caractéristiques principales de cette réaction.
1.3.2.2 Indiquer les noms des composés $(D)$ et $(F)$ qui peuvent réagir totalement avec l'alcool $(B)$ pour obtenir le même ester $(E).$
Écrire les équations bilans des réactions correspondantes.
1.3.3 L'action de l'acide $(C)$ sur la $N-$méthyléthanamine donne un composé ionique $G$, qui est ensuite déshydraté par chauffage prolongé pour donner un composé organique $H.$
Écrire l'équation bilan de la réaction.
Donner la formule semi développée et le nom du composé $H$ obtenu.
Exercice 2
L'acide acétylsalicylique ou aspirine de formule brute $C_{9}H_{8}O_{4}$ est l'un des médicaments les plus utilisés, pour ses effets calmants et curatifs sur de multiples pathologies.
On se propose dans une première étape de vérifier, par dosage, la masse d'acide acétylsalicylique contenue dans un comprimé d'aspirine dont l'indication sur l'étiquette est << Aspirine $500\,mg$>>, puis d'étudier, dans une seconde étape, l'évolution temporelle de sa réaction avec les ions hydrogénocarbonate $HCO_{3}^{-}.$
2.1 Dosage d'une solution d'acide acétylsalicylique
On dissout un comprimé d'aspirine dans de l'eau distillée.
On obtient ainsi une solution aqueuse $S$ d'acide acétylsalicylique de concentration molaire volumique $C_{A}$, de volume $V=278\,ml.$
On prélève un volume $V_{A}=10\,mL$ de la solution $S$ qu'on dose par une solution aqueuse $S_{B}$ d'hydroxyde de sodium de concentration $C_{B}=10^{-2} mol\cdot L^{-1}$ en utilisant un indicateur coloré convenable.
2.1.1 Écrire l'équation de la réaction support du dosage.
$($On notera par $AH$ l'acide acétylsalicylique et $A^{-}$ sa base conjuguée$).$
Pour obtenir l'équivalence, il faut verser un volume $V_{BE}=10\,mL$ de la solution $S_{B}.$
2.1.2 Déterminer la concentration $C_{A}$ de la solution $S_{B}.$
2.1.3 Déterminer la masse d'acide acétylsalicylique contenue dans le comprimé.
L'indication sur l'étiquette <<Aspirine $500\,mg$>> est-elle vérifiée ?
2.2 Étude de la réaction entre les ions hydrogénocarbonate et l'acide acétylsalicylique
Afin de suivre l'évolution de cette réaction, on introduit dans un ballon, un volume $v=10\,mL$ d'une solution aqueuse d'hydrogénocarbonate de sodium $\left(HCO_{3}^{-}+Na^{+}\right)$ dont la concentration initiale en ions hydrogénocarbonate est $C=0.5 mol\cdot L^{-1}.$
A un instant choisi comme origine des dates $(t=0)$, on ajoute dans le ballon une quantité d'acide acétylsalicylique de masse $m=0.5\,g.$
$\left(\text{On considère que le volume du mélange réactionnel reste constant }V=10\,mL\right).$
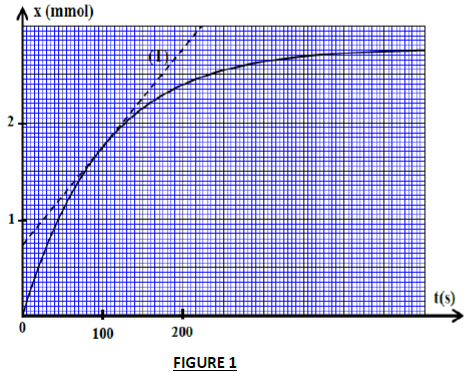
La courbe de la figure ci-dessous (figure 1) représente l'évolution temporelle de la quantité de matière $x$ de $CO_{2}$ formée lors de la réaction.
2.2.1 Écrire l'équation de la réaction chimique entre les ions hydrogénocarbonate $HCO_{3}^{-}$ et l'acide acétylsalicylique, supposée totale.
On donne les couples $C_{9}H_{8}O_{4}/C_{9}H_{7}O_{4}^{-}$ et $CO_{2}$, $H_{2}O/HCO_{3}^{-}$
2.2.2 Déterminer graphiquement la valeur de la quantité de matière de $CO_{2}$ maximale.
2.2.3 Déterminer graphiquement la vitesse volumique de la réaction à l'instant $t=100 s.$
$(T)$ représente la tangente à la courbe à l'instant $t=100s.$
2.2.4 Déterminer graphiquement le temps de demi réaction $\tau.$
Exercice 3
Une oxygénation correcte de l'eau est importante à la fois pour les poissons et pour certaines bactéries.
Le système d'oxygénation de l'eau d'un aquarium est constitué d'une pompe à air et d'un diffuseur qui produit de petites bulles d'air sphériques qui remontent verticalement vers la surface.
On étudie ici le mouvement d'une de ces bulles d'air de masse $m$, de rayon $r$ et de masse volumique $\rho=1.3\,kg\cdot m^{-3}$ suivant un axe $(OZ)$ vertical orienté vers le haut (figure 2).
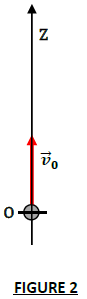
A la date $t=0$, son centre d'inertie coïncide avec l'origine de l'axe et sa vitesse est $\overrightarrow{v}_{0}.$
L'origine $O$ de l'axe se situe au fond de l'aquarium.
La bulle est soumise à son poids, à la poussée d'Archimède et à une force de frottement fluide de la forme $\overrightarrow{f}=-k\overrightarrow{V}$ avec $k=6\pi\eta r$ et $\eta$ la viscosité de l'eau.
On suppose que la bulle conserve le même volume durant toute la remontée $\left(V_{B}=\dfrac{4}{3}\pi r^{3}\right)$
La masse volumique de l'eau est $\rho_{e}=1.0kg\cdot L^{-1}$ et la viscosité de l'eau $\eta=1.2\cdot 10^{-3}S.I.$
On prendra $g=10\,m\cdot s^{-2}.$
3.1 Représenter sur un schéma les forces appliquées à la bulle.
3.2 En appliquant le théorème du centre d'inertie à la bulle, établir l'équation différentielle relative à la vitesse $v$ de la bulle.
3.3 Au bout d'un temps suffisamment long, l'accélération s'annule et la vitesse atteint une valeur limite appelée vitesse limite $V_{l}.$
3.3.1 Établir l'expression de la vitesse limite en fonction de $k$, $\rho_{e}$, $\rho$, $r$ et $g.$
3.3.2 La vitesse limite atteinte par la bulle est $V_{L}=2\,m\cdot S^{-1}$, calculer le rayon $r$ de la bulle.
3.4 Mettre l'équation différentielle établie en 3.2 sous la forme : $\dfrac{\mathrm{d}v}{\mathrm{d}t}+a V=aV_{L}$ où $\alpha$ est une constante qu'on exprimera en fonction de $k$, $\rho$, et $r.$
Calculer $\alpha.$
3.5 Montrer que la solution de l'équation différentielle peut se mettre sous la forme : $V=A\mathrm{e}^{-\alpha t}+B.$
On exprimera les constantes $A$ et $B$ en fonction de $V_{L}$ et $v_{0}.$
3.6. On considère maintenant que la vitesse de diffusion $v_{0}$ est nulle.
Le temps caractéristique du mouvement ou constante de temps, noté $\tau$, est la durée au bout de laquelle la vitesse atteint $63\%$ de sa valeur limite.
On pourra considérer que la vitesse limite est atteinte au bout d'une durée $\Delta t=5\tau$
3.6.1 Calculer ce temps caractéristique $\tau.$
Trouver la relation entre $\alpha$ et $\tau.$
1.3.6.2 A la date $t=0.3\,s$ la bulle atteint le bord supérieur de l'aquarium.
Déterminer la hauteur $H$ de l'aquarium.
Exercice 4
En électricité, un circuit $RLC$ est un circuit linéaire contenant un résistor, une bobine inductive et un condensateur.
Il existe deux types de circuits $RLC$, série ou parallèle selon l'interconnexion des trois types de composants.
Le comportement d'un circuit $RLC$ est généralement décrit par une équation différentielle.
On étudie un dipôle $(RLC)$ constitué de l'association en série d'un condensateur de capacité $C$, d'une bobine d'inductance $l$ et de résistance $r$ et un résistor de résistance $R=300\Omega.$
L'ensemble est alimenté par un générateur basse fréquence $(GBF)$ délivrant à ses bornes une tension sinusoïdale $u(t)=U_{m}\cdot\sin(2\pi Nt)$ d'amplitude constante et de fréquence $N$ réglable.
Un oscilloscope bicourbe est connecté au circuit comme l'indique la figure 3.
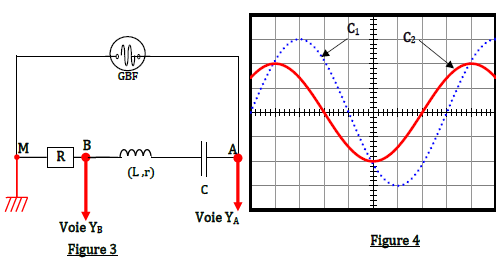
Base de temps : $2\,ms/\text{division}$
Sensibilité verticale : $\left(C_{1}\right)$ : $2\,V/\text{division}$
Sensibilité verticale : $\left(C_{2}\right)$ : $5\,V/\text{division}$
4. La fréquence du $GBF$ étant fixée à une valeur $N_{1}$, on obtient les oscillogrammes $\left(C_{1}\right)$ et $\left(C_{2}\right)$ de la figure 4.
4.1.1 Préciser la tension visualisée sur chaque voie.
Déterminer la fréquence $N_{1}$ des tensions visualisées.
4.1.2 Pour chaque voie, attribuer l'oscillogramme correspondant.
Quelle est la courbe qui permet de suivre l'évolution de l'intensité du courant traversant le circuit.
4.1.3 Déterminer l'amplitude $l_{m}$ de l'intensité du courant traversant le circuit.
En déduire l'impédance $Z$ du circuit.
4.1.4 Trouver le déphasage de $\Delta\phi=\phi_{i}-\phi_{u}$ de $i(t).$ par rapport à $u(t).$
En déduire le caractère inductif ou capacitif du circuit.
Écrire l'expression $i(t)$ de l'intensité du courant.
4.1.5 Calculer le facteur de puissance puis trouver la valeur de la résistance $r$ de la bobine.
4.2 Pour étudier le comportement du dipôle $(RLC)$ pour une autre fréquence $N_{2}$ du $GBF$, on modifie les branchements de l'oscilloscope dans le circuit précèdent et on visualise la tension $u(t)$ aux bornes du $GBF$ sur la voie $Y_{A}$ et la tension $u_{c}(t)$ aux bornes du condensateur sur la voie $Y_{B}.$
Les oscillogrammes $\left(C_{3}\right)$ et $\left(C_{4}\right)$ de la figure 5 sont visualisés sur l'écran de l'oscilloscope.
4.2.1 Reprendre le schéma du circuit (figure 3) et y faire figurer les branchements convenables de l'oscilloscope.
Attribuer à chaque oscillogramme la tension correspondante.
4.2.2 Déterminer le déphasage $\Delta\phi'=\phi_{u_{c}}-\phi_{u}$ de $u_{c}(t)$ par rapport à $u(t)$ puis montrer que le circuit est à la résonance d'intensité.
4.2.3 Déterminer la valeur de l'intensité qu'indiquerait un ampèremètre branché en série dans le circuit puis calculer la capacité $C$ du condensateur et l'inductance $L$ de la bobine.
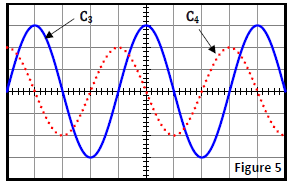
Base de temps : $1\,ms/\text{division}$
Sensibilité vertical $\left(C_{3}\right)\ :\ 5\,V/\text{division}$
Sensibilité vertical $\left(C_{4}\right)\ :\ 5\,V\text{division}$
Exercice 5
Données : $1_{u}=931.5\,Mev/C^{2}$
Dans le site de Diogo, au Sénégal, le consortium Grande Côte Opération $(GCO)$ a exploité $5500\text{tonnes}$ de zircon en Avril $2014.$
Le zirconium est l'élément chimique de symbole $Zr$, de numéro atomique $40.$
Il est extrait du minerai de zircon sous forme d'oxyde de formule $ZrSiO_{4}.$
Après une double désintégration $\beta$, l'isotope $^{96}Zr$ donne un noyau fils $_{Z'}^{A'}Y.$
Nous notons $N_{0}$ le nombre de noyau de zirconium radioactif présent à l'instant initial $t_{0}=0$, et par $N$ le nombre de noyau radioactif restant à l'instant $t$ dans le minerai.
5.1 Donner la composition du noyau de l'isotope $^{96}Zr$ du zirconium.
5.2 La masse d'un noyau de zirconium $96$ est de $95.908_{u}.$
Calculer en $MeV$, l'énergie de liaison $E_{l}$ d'un noyau de zirconium $96.$
En déduire son énergie de liaison par nucléon $E_{A}$ en $MeV/\text{nucléon}.$
5.3 Écrire l'équation-bilan de la réaction de désintégration du zirconium $96$ sachant qu'elle libère deux particules $\beta.$
Identifier le noyau fis.
$$\begin{array}{|l|c|c|c|c|c|} \hline t\left(10^{-3}\,\text{an}\right)&1&2&3&4&5\\ \hline \ln\left(\dfrac{N_{0}}{N}\right)\left(10^{-23}\right)&3.46&6.92&10.4&13.8&17.3\\ \hline \end{array}$$
5.4 Des mesures ont permis de dresser le tableau ci-dessous :
5.4.1 Tracer le graphe $\ln\left(\dfrac{N_{0}}{N}=f(t)\right).$
Échelle : $2\,cm\ \longrightarrow\ 10^{-3}\text{an}$ ;
$1\,cm\ \longrightarrow\ 2\cdot 10^{-23}$
5.4.2 Déterminer la relation numérique entre $\ln\left(\dfrac{N_{0}}{N}\right)$ et $t.$
En déduire la période radioactive $T$ du zirconium étudié.
5.4.3 Au bout de combien de temps le quart des noyaux radioactifs initialement présent se sont-ils désintégrés ?
$$\begin{array}{|l|l|l|l|l|l|l|} \hline \text{Nom (symbole)}&\text{Strontium }(Sr)&\text{Molybdéne }(Mo)&\text{Plutinium }(Pu)&\text{Curium }(Cm)&\text{Proton}&\text{Neutron}\\ \hline \text{Numéro atomique}&38&42&94&96&1&0\\ \text{Masse en }u&87062&95.96&244.0&247.0&1.0073&1.0086\\ \hline \end{array}$$

Ajouter un commentaire