Bac Maths, S Métropole 11 mai 2022
Sujet 1
Épreuve d'enseignement de spécialité
Le sujet propose $4$ exercices
Le candidat choisit $3$ exercices parmi les $4$ et ne doit traiter que ces $3$ exercices
Exercice 1 Thèmes : fonction exponentielle, suites
Dans le cadre d'un essai clinique on envisage deux protocoles de traitement d'une maladie.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en $mg$, par la fonction $f$ définie sur l'intervalle $[0\ ;\ 10]$ par $$f(t)=3t\mathrm{e}^{-0.5t+1}$$
où $t$ désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
1. a. On admet que la fonction $f$ est dérivable sur l'intervalle $[0\ ;\ 10]$ et on note $f'$ sa fonction dérivée.
Montrer que, pour tout nombre réel $t$ de $[0\ ;\ 10]$, on a : $f'(t)=3(-0.5t+1)\mathrm{e}^{-0.5t+1}.$
b. En déduire le tableau de variations de la fonction $f$ sur l'intervalle $[0\ ;\ 10].$
c. Selon cette modélisation, au bout de combien de temps la quantité de médicament présente dans le sang du patient sera-t-elle maximale ?
Quelle est alors cette quantité maximale ?
2. a. Montrer que l'équation $f(t)=5$ admet une unique solution sur l'intervalle $[0\ ;\ 2]$ notée $\alpha$, dont on donnera une valeur approchée à $10^{-2}$ près.
On admet que l'équation $f(t)=5$ admet une unique solution sur l'intervalle $[2\ ;\ 10]$, notée $\beta$, et qu'une valeur approchée de $\beta$ à $10^{-2}$ près est $3.46.$
b. On considère que ce traitement est efficace lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à $5mg.$
Déterminer, à la minute près, la durée d'efficacité du médicament dans le cas de ce protocole.
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqûre intraveineuse, une dose de $2\,mg$ de médicament puis à réinjecter toutes les heures une dose de $1.8\,mg.$
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de $30\%$ par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite $\left(u_{n}\right)$ où, pour tout entier naturel $n$, $u_{n}$ désigne la quantité de médicament, exprimée en $mg$, présente dans le sang du patient immédiatement après l'injection
de la $n^{ième}$ heure.
On a donc $u_{0}=2.$
1. Calculer, selon cette modélisation, la quantité $u_{1}$, de médicament $($en $mg)$ présente dans le sang du patient immédiatement après l'injection de la première heure.
2. Justifier que, pour tout entier naturel $n$, on a : $u_{n+1}=0.7u_{n}+1.8.$
3. a. Montrer par récurrence que, pour tout entier naturel $n$, on a : $u_{n}\leq u_{n+1}<6.$
b. En déduire que la suite $\left(u_{n}\right)$ est convergente.
On note $\ell$ sa limite.
c. Déterminer la valeur de $\ell.$
Interpréter cette valeur dans le contexte de l'exercice.
4. On considère la suite $\left(v_{n}\right)$ définie, pour tout entier naturel $n$, par $v_{n}=6-u_{n}.$
a. Montrer que la suite $\left(v_{n}\right)$ est une suite géométrique de raison $0.7$ dont on précisera le premier terme.
b. Déterminer l'expression de $v_{n}$ en fonction de $n$, puis de $u_{n}$ en fonction de $n.$
c. Avec ce protocole, on arrête les injections lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à $5.5\,mg.$
Déterminer, en détaillant les calculs, le nombre d'injections réalisées en appliquant ce protocole.
Exercice 2 Thème : géométrie dans l'espace
Dans l'espace rapporté à un repère orthonormé $\left(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}\right)$, on considère :
$\bullet\ $le point $A$ de coordonnées $(-1\ ;\ 1\ ;\ 3)$
$\bullet\ $la droite $\mathcal{D}$ dont une représentation paramétrique est : $\left\lbrace\begin{array}{lcl} x&=&1+2t\\y&=&2-t\;,\quad t\in\mathbb{R}\\z&=&2+2t \end{array}\right.$
On admet que le point $A$ n'appartient pas à la droite $\mathcal{D}.$
1. a. Donner les coordonnées d'un vecteur directeur $\overrightarrow{u}$ de la droite $\mathcal{D}.$
b. Montrer que le point $B(-1\ ;\ 3\ ;\ 0)$ appartient à la droite $\mathcal{D}.$
c. Calculer le produit scalaire $\overrightarrow{AB}\cdot\overrightarrow{u}.$
2. On note $\mathfrak{P}$ le plan passant par le point $A$ et orthogonal à la droite $\mathcal{D}$, et on appelle $H$ le point d'intersection du plan $\mathfrak{P}$ et de la droite $\mathcal{D}.$
Ainsi, $H$ est le projeté orthogonal de $A$ sur la droite $\mathcal{D}.$
a. Montrer que le plan $\mathfrak{P}$ admet pour équation cartésienne : $2x-y+2z-3=0.$
b. En déduire que le point $H$ a pour coordonnées $\left(\dfrac{7}{9}\ ;\ \dfrac{19}{9}\ ;\ \dfrac{16}{9}\right)$
c. Calculer la longueur $AH.$
On donnera une valeur exacte.
3. Dans cette question, on se propose de retrouver les coordonnées du point $H$, projeté orthogonal du point $A$ sur la droite $\mathcal{D}$, par une autre méthode.
On rappelle que le point $B(-1\ ;\ 3\ ;\ 0)$ appartient à la droite $\mathcal{D}$ et que le vecteur $\overrightarrow{u}$ est un vecteur directeur de la droite $\mathcal{D}.$
a. Justifier qu'il existe un nombre réel $k$ tel que $\overrightarrow{HB}=k\overrightarrow{u}.$
b. Montrer que $k=\dfrac{\overrightarrow{HB}\cdot\overrightarrow{u}}{||\overrightarrow{u}||^{2}}.$
c. Calculer la valeur du nombre réel $k$ et retrouver les coordonnées du point $H.$
4. On considère un point $C$ appartenant au plan $\mathfrak{P}$ tel que le volume du tétraèdre $ABCH$ soit égal à $\dfrac{8}{9}$
Calculer l'aire du triangle $ACH.$
On rappelle que le volume d'un tétraèdre est donné par : $V=\dfrac{1}{3}\times\mathfrak{B}\times h$ où $\mathfrak{B}$ désigne l'aire d'une base et $h$ la hauteur relative à cette base.
Exercice 3 Thème : probabilités
Le directeur d'une grande entreprise a proposé à l'ensemble de ses salariés un stage de formation à l'utilisation d'un nouveau logiciel.
Ce stage a été suivi par $25\%$ des salariés.
1. Dans cette entreprise, $52\%$ des salariés sont des femmes, parmi lesquelles $40\%$ ont suivi le stage.
On interroge au hasard un salarié de l'entreprise et on considère les évènements :
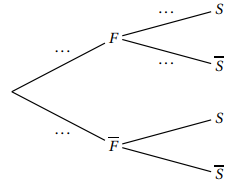
$\bullet\ F$ : « le salarié interrogé est une femme »,
$\bullet\ S$ : « le salarié interrogé a suivi le stage ».
$\overline{F}$ et $\overline{S}$ désignent respectivement les évènements contraires des évènements $F$ et $S.$
a. Donner la probabilité de l'évènement $S.$
b. Recopier et compléter les pointillés de l'arbre pondéré ci-dessous sur les quatre branches indiquées.

c. Démontrer que la probabilité que la personne interrogée soit une femme ayant suivi le stage est égale à $0.208.$
d. On sait que la personne interrogée a suivi le stage.
Quelle est la probabilité que ce soit une femme ?
e. Le directeur affirme que, parmi les hommes salariés de l'entreprise, moins de $10\%$ ont suivi le stage.
Justifier l'affirmation du directeur.
2. On note $X$ la variable aléatoire qui à un échantillon de $20$ salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage.
On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
a. Déterminer, en justifiant, la loi de probabilité suivie par la variable aléatoire $X.$
b. Déterminer, à $10^{-3}$ près, la probabilité que $5$ salariés dans un échantillon de $20$ aient suivi le stage.
c. Le programme ci-dessous, écrit en langage Python, utilise la fonction binomiale $(i\;,\ n\;,\ p)$ créée pour l'occasion qui renvoie la valeur de la probabilité $P(X=i)$ dans le cas où la variable aléatoire $X$ suit une loi binomiale de paramètres $n$ et $p.$
$$\boxed{\text{def proba}(k)\\\\P=0\\\\\text{for i in range }(0\;,\ k+1)\ :\\\\ P=P+\text{binomiale }(i\;,\ 20\;,\ 0.25)\\\\\text{return }P}$$
Déterminer, à $10^{-3}$ près, la valeur renvoyée par ce programme lorsque l'on saisit proba $(5)$ dans la console Python.
Interpréter cette valeur dans le contexte de l'exercice.
d. Déterminer, à $10^{-3}$ près, la probabilité qu'au moins $6$ salariés dans un échantillon de $20$ aient suivi le stage.
3. Cette question est indépendante des questions 1 et 2.
Pour inciter les salariés à suivre le stage, l'entreprise avait décidé d'augmenter les salaires des salariés ayant suivi le stage de $5\%$, contre $2\%$ d'augmentation pour les salariés n'ayant pas suivi le stage.
Quel est le pourcentage moyen d'augmentation des salaires de cette entreprise dans ces conditions ?
Exercice 4 Thème : fonctions numériques
Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte.
Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
1. La courbe représentative de la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\dfrac{-2x^{2}+3x-1}{x^{2}+1}$ admet pour asymptote la droite d'équation :
a. $x=-2$
b. $y=-1$
c. $y=-2$
d. $y=0$
2. Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x\mathrm{e}^{x^{2}}.$
La primitive $F$ de $f$ sur $\mathbb{R}$ qui vérifie $F(0)=1$ est définie par :
a. $F(x)=\dfrac{x^{2}}{2}\mathrm{e}^{x^{2}}$
b. $F(x)=\dfrac{1}{2}\mathrm{e}^{x^{2}}$
c. $F(x)=\left(1+2x^{2}\right)\mathrm{e}^{x^{2}}$
d. $F(x)=\dfrac{1}{2}\mathrm{e}^{x^{2}}+\dfrac{1}{2}$
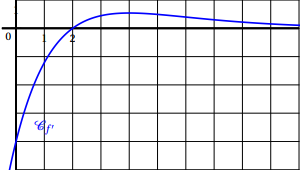
3. On donne ci-dessous la représentation graphique $\mathcal{C}_{f'}$ de la fonction dérivée $f'$ d'une fonction $f$ définie sur $\mathbb{R}.$

On peut affirmer que la fonction $f$ est :
a. concave sur $]0\ ;\ +\infty[$ ;
b. convexe sur $]0\ ;\ +\infty[$ ;
c. convexe sur $[0\ ;\ 2]$ ;
d. convexe sur $[2\ ;\ +\infty[.$
4. Parmi les primitives de la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=3\mathrm{e}^{-x^{2}}+2$ :
a. toutes sont croissantes sur $\mathbb{R}$ ;
b. toutes sont décroissantes sur $\mathbb{R}$ ;
c. certaines sont croissantes sur $\mathbb{R}$ et d'autres décroissantes sur $\mathbb{R}$ ;
d. toutes sont croissantes sur $]-\infty\ ;\ 0]$ et décroissantes sur $[0\ ; +\infty[.$
5. La limite en $+\infty$ de la fonction $f$ définie sur l'intervalle $]0\ ;\ +\infty[$ par $f(x)=\dfrac{2\ln x}{3x^{2}+1}$ est égale à :
a. $\dfrac{2}{3}$ ;
b. $+\infty$ ;
c. $-\infty$ ;
d. $0.$
6. L'équation $\mathrm{e}^{2x}+\mathrm{e}^{x}-12=0$ admet dans $\mathbb{R}$ :
a. trois solutions ;
b. deux solutions ;
c. une seule solution ;
d. aucune solution.

Ajouter un commentaire