Bac Maths D, Maroc 2018

Dans l'espace rapporté à un repère orthonormé direct $(O\ ;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$, on considère la sphère $(S)$ de centre $\Omega(2\ ;\ 1\ ;\ 2)$ et de rayon égale à $3$ et le plan $(\mathcal{P})$ passant par le point $A(-1\ ;\ 0\ ;\ 3)$ et $\vec{U}(4\ ;\ 0\ ;\ -3)$ est un vecteur normal à $(\mathcal{P}).$

1. Montrer que $x^{2}+y^{2}+z^{2}-4x-2y-4z=0$ est une équation cartésienne de la sphère $(S).$
 
2. Vérifier que $4x-3z+13=0$ est une équation cartésienne du plan $(\mathcal{P})$

3. a) Vérifier que
$$\left\lbrace\begin{array}{lcl} x&=&2+4t\\  y&=&1\quad(t\in\mathbb{R})\text{ est une représentation paramétrique de la droite}\\ z&=&2-3t\\ \end{array}\right\rbrace$$

$(\Delta)$ passant par $\Omega$ et orthogonale à $(\mathcal{P})$

b) Déterminer les coordonnées de $H$ point d'intersection de la droite $(\Delta)$ et du plan $(\mathcal{P}).$

4. a) Calculer $d(\Omega\;,\ (\mathcal{P})).$

b) Montrer que le plan $(\mathcal{P})$ est tangent à la sphère $(S)$ en un point que l'on déterminera.

1. Résoudre dans l'ensemble $\mathbb{C}$ des nombres complexes l'équation : $z^{2}-2\sqrt{2}z+0=0$

2. Dans le plan complexe rapporté à un repère orthonormé $(O\ ;\ \vec{u}\;,\ \vec{v})$, on considère le point $A$ d'affixe $a=\sqrt{2}(1-\mathrm{i})$ et la rotation $R$ de centre $O$ et d'angle $\dfrac{\pi}{3}.$

a) Écrire sous forme trigonométrique le nombre complexe $a.$

b) Vérifier que l'affixe du point $B$ image du point $A$ par la rotation $R$ est :
$$b=2\left(\cos\left(\dfrac{\pi}{12}\right)+\mathrm{i}\sin\left(\dfrac{\pi}{12}\right)\right)$$

3. a) On considère le point $C$ d'affixe $c=1+\mathrm{i}.$

Montrer que $b^{2}-c^{2}=2\sqrt{3}.$

b) Soit $t$ la translation du vecteur $\overrightarrow{OC}$ et $D$ l'image de $B$ par la translation $T.$

Montrer que $OD=|b+c|$

c) En déduire que $OD\times BC=2\sqrt{3}.$

Une urne contient $12$ boules indiscernables au toucher :

$3$ boules rouges portant chacune le nombre $1,\ 3$ boules rouges portant chacune le nombre $2$ et $6$ boules vertes portant chacune le nombre $2.$

On tire au hasard et simultanément deux boules de l'urne, et on considère les évènements suivants :

$A$ : les deux boules tirées portent le même nombre

$B$ : les deux boules tirées sont de couleurs différentes  

$C$ : les deux boules tirées portent deux nombres dont la somme est égale à $3.$

1. Montrer que $p(A)=\dfrac{13}{22}$ et $p(B)=\dfrac{6}{11}$ puis calculer $p(C)$

2. a) Montrer que $p(A\cap B)=\dfrac{3}{11}$
                                                                                                   
b) Les deux évènements $A$ et $B$ sont-ils indépendants ? Justifier votre réponse.

3. Sachant que l'évènement $B$ est réalisé, calculer la probabilité de tirer deux boules portant le même nombre.

1. a) Montrer que la fonction $H\ ∶\ x\longmapsto x\mathrm{e}^{x}$ est une primitive de la fonction $h\ ∶\ x\longmapsto(x+1)\mathrm{e}^{x}$ sur $\mathbb{R}$  

b) En déduire que $$\int^{1}_{0}(x+1)\mathrm{e}^{x}\mathrm{d} x=\mathrm{e}$$
                                                                                               
2. a) A l'aide d'une intégration par partie, calculer $$\int^{1}_{0}(x+1)\mathrm{e}^{x}\mathrm{d}x$$  

A) Soit $g$ la fonction numérique définie sur l'intervalle $]0\ ;\ +\infty[$ par : $$g(x)=x^{3}-1-2\ln^{2}x +2\ln x$$

Le tableau ci-dessous est le tableau de variation de la fonction $g$ sur l'intervalle $]0\ ;\ +\infty[$
$$\begin{array}{|c|lcr|} \hline x&0& &+\infty\\ \hline g'(x)& &+&\\ \hline & &&+\infty\\ g(x)& &\nearrow&\\ &-\infty&&\\ \hline \end{array}$$

1. Calculer $g(1)$

2. Déterminer, à partir de ce tableau, le signe de $g(x)$ sur chacun des intervalles $]0\ ;\ 1]$ et $]1\ ;\ +\infty[$                             

B) On considère la fonction numérique $f$ définie sur l'intervalle $]0\ ;\ +\infty[$ par :
$$f(x)=x-\dfrac{1}{2}+\dfrac{1}{2x^{2}}+\left(\dfrac{\ln x}{x}\right)^{2}$$

Soit $(\mathcal{C})$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$

1. a) Vérifier que $\lim\limits_{x\rightarrow +\infty}f(x)=+\infty$

b) Montrer que la droite $(D)$ d'équation $y=x-\dfrac{1}{2}$ est une asymptote à la courbe $(\mathcal{C})$ au voisinage de $+\infty.$

c) Dresser la position relative de la droite $(D)$ et la courbe $(\mathcal{C}).$

2. Montrer que $\lim\limits_{x\rightarrow 0^{+}}f(x)=+\infty$ et interpréter le résultat géométriquement.

3. a) Montrer que $f'(x)=\dfrac{g(x)}{x}$ pour tout $x$ de l'intervalle $]0\ ;\ +\infty[$                            

b) Montrer que la fonction $f$ est décroissante sur l'intervalle $]0\ ;\ 1]$ et croissante sur l'intervalle $[1\ ;\ +\infty[$
   
c) Dresser le tableau de variation de la fonction $f$ sur l'intervalle $]0\ ;\ +\infty[$
   
4. Construire dans le repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$, la droite $(D)$ et la courbe $(\mathcal{C})$ $($unité : $1\,cm)$

C) On considère la fonction numérique $h$ définie sur $]0\ ;\ +\infty[$ par : $$h(x)=f(x)-x$$

1. a) Vérifier que $h(1)=0$

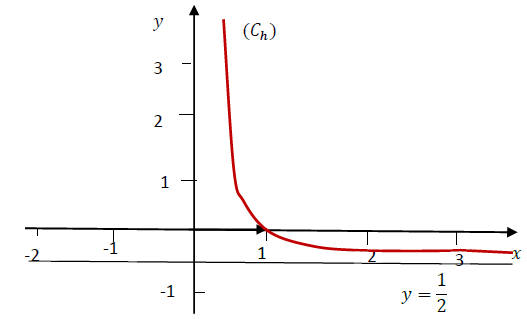
b) Dans la figure ci-dessous, $\left(\mathcal{C_{h}}\right)$ est la représentation graphique de la fonction $h.$

Déterminer le signe de $h(x)$ sur chacun des intervalles $]0\ ;\ 1]$ et $[1\ ;\ +\infty[$ puis en déduire que : $f(x)\leq x$ pour tout $x$ de l'intervalle $[1\ ;\ +\infty[$  

2. On considère la suite numérique $\left(U_{n}\right)$ définie par : $U_{0}=\mathrm{e}$ et $U_{n+1}=f\left(U_{n}\right)$ pour tout $n\in\mathbb{N}$

a) Montrer par récurrence que $1\leq U_{n}\leq\mathrm{e}$ pour tout $n\in\mathbb{N}$

b) Montrer que la suite $\left(U_{n}\right)$ est croissante.

(On pourra utiliser le résultat de la question C) 1. b))

3. En déduire que la suite $\left(U_{n}\right)$ est convergente et déterminer sa limite.