Bac Math 2e groupe S1 S3 2009

1) On considère un triangle $EFG$ tel que :

$$\left\lbrace\begin{array}{lcl} FG &=& \sqrt{2}EF \\ \\ \left(\overrightarrow{FE}\;,\ \overrightarrow{FG}\right) &=& \dfrac{\pi}{4} \end{array}\right.$$

 

a) Montrer que $EF=EG.$

 

[ On pourra calculer $EG^{2}$ en utilisant la relation $\overrightarrow{EG}=\overrightarrow{EF}+

\overrightarrow{FG}]\quad(1\;pt)$

 

b) En déduire que le triangle $EFG$ est rectangle et isocèle.$\quad(0.5\;pt)$

 

2) Dans le plan orienté on considère un triangle $ABC$, rectangle et isocèle en $A$; on suppose que $\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)=\dfrac{\pi}{2}\;[2\pi]$

 

On note $A'$ le symétrique de $A$ par rapport au point $C.$

 

a) Déterminer le rapport et l'angle de la similitude directe $s$ qui transforme $A'$ en $C$ et $C$ en $B.\quad(0.5+0.5=1\;pt)$

 

b) Soit $\Omega$ le centre de la similitude $s.$ Démontrer que le triangle $\Omega CB$ est direct, rectangle et isocèle.$\quad(1\;pt)$

 

c) En déduire une construction de $\Omega\quad(0.5\;pt)$

 

1) Déterminer la solution $f$ de l'équation différentielle $$(E)\ :\ y''+4y'+4y=0$$ vérifiant la condition initiale $f(0)=0$ et $f'(0)=1.\quad(1\;pt)$

 

2) Soit $g$ la fonction définie par : $g(x)= (x+3)\mathrm{e}^{-2x}.$

 

a) Montrer que $g$ est une solution de $(E)\quad(0.5\;pt)$

 

b) Déterminer une primitive $G$ de $g$ en utilisant :

 

i : l'équation différentielle $(E).\quad(0.75\;pt)$

 

ii : une intégration par parties.$\quad(0.75\;pt)$

 

3) Soit $F$ la fonction définie par :

$$F(x)=-\dfrac{1}{4}(2x+1)\mathrm{e}^{-2x}+\dfrac{1}{4}$$

 

a) Montrer que la restriction $H$ de $F$ à $[0\;,\ +\infty[$ est une bijection de $[0\;,\ +\infty[$ sur un intervalle à préciser.$\quad(0.5\;pt)$

 

b) Déterminer l'ensemble de dérivabilité de $H^{-1}$, fonction réciproque de $H.\quad(0.5\;pt)$

 

1) En utilisant l'algorithme d'Euclide déterminer le pgcd de 231 et 3311.$\quad(1\;pt)$

 

2) Soit $n$ un entier naturel supérieur ou égal à 2. On pose :

$$A_{n}=1+2+\cdots+n\;\text{ et }\;B_{n}=1^{2}+2^{2}+\cdots+n^{2}$$

 

Démontrer que $$ A_{n}=\dfrac{1}{2}n(n+1)\;\text{ et }\;B_{n}=\dfrac{1}{6}n(n+1)(2n+1)\quad(2\times 0.5=1\;pt)$$

 

3) a) Démontrer que pour tout $k\in\;\mathbb{Z}\;,\ \dfrac{1}{2}k(3k+1)$ est un entier.$\quad(0.5\;pt)$

 

b) On suppose que $n$ est un multiple de 3. Déterminer le pgcd de $A_{n}$ et $B_{n}.\quad(1\;pt)$

 

4) Vérifier le résultat obtenu dans le cas où $n=21.\quad(0.5\;pt)$

 

Dans le plan complexe on considère l'application $\varphi$ qui, à tout point $M$ d'affixe $z$ non nulle, on associe le point $M'$ d'affixe $z'$ telle que :

$$z'=-\dfrac{1}{2}\left(z-\dfrac{1}{z}\right)$$

 

On note $A$ le point d'affixe $\mathrm{i}$

 

1) Déterminer l'affixe de $A'$ image de $A$ par $\varphi.\quad(1\;pt)$

 

2) Montrer que $\dfrac{z'+\mathrm{i}}{z'-\mathrm{i}}=\dfrac{1}{2}\left(\dfrac{z+\mathrm{i}}{z-\mathrm{i}}\right)^{2}$,

pour tout $z$ distinct de $\mathrm{i}$ et de $-\mathrm{i}.\quad(1\;pt)$

 

3) En déduire $(\overrightarrow{M'A}\;,\ \overrightarrow{M'A'})$ en fonction de $(\overrightarrow{MA}\;,\ \overrightarrow{MA'})\quad(1\;pt)$

 

4) Déterminer l'ensemble des points $M$ tels que $(\overrightarrow{M'A}\;,\ \overrightarrow{M'A'})=\pi\;[2\pi]\quad(1\;pt)$

 

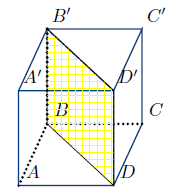
Soit $ABCDA'B'C'D'$ un cube (Voir figure ci-contre).

 

On désigne par :

 

$s_{1}$ réflexion de base le plan $(AA'B'B).$

 

$s_{2}$ réflexion de base le plan $(BB'CC').$

 

$s_{3}$ réflexion de base le plan $(CC'DD').$

 

$s_{4}$ réflexion de base le plan $(DD'AA').$

 

1) a) Montrer que $r=s_{2}\circ s_{1}$ est un demi tour dont on précisera l'axe.$\quad(1\;pt)$

 

b) Déterminer la nature et les éléments géométriques caractéristiques de $r'=s_{4}\circ s_{3}.\quad(1\;pt)$

 

2) On note $s$ la réflexion de base le plan $(BB'DD').$

 

a) Déterminer les réflexions $s'$ et $s''$ telles que $r=s\circ s'$ et $r'=s''\circ s.\quad(1\;pt)$

 

b) En déduire que $t=r'\circ r$ est la translation de vecteur $2\overrightarrow{BD}.\quad(1\;pt)$