Corrigé BFEM Physique chimie 2018
Exercice 1
1.1) Recopions puis complétons les phrases suivantes :
Les hydrocarbures sont des composés organiques uniquement constitués des éléments carbone et hydrogène.
L'éthane, de formule brute $C_{2}H_{6}$ et le méthane de formule brute $CH_{4}$ sont des hydrocarbures appartenant à la famille des alcanes.
L'hydrocarbure de formule $C_{2}H_{4}$ appartient à la famille des alcènes alors que l'éthyne de formule brute $C_{2}H_{2}$ est de la famille des alcynes.
1.2) Répondons par $\text{Vrai}$ ou $\text{Faux}$
1.2.1) Le dioxygène de l'air n'attaque pas l'aluminium à froid $\quad\text{Vrai}$
1.2.2) La réaction entre une solution acide et une solution basique est exothermique $\quad\text{Vrai}$
1.2.3) Le bleu de bromothymol est bleu en milieu neutre $\quad\text{Faux}$
1.2.4) L'acide chlorhydrique dilué et à froid réagit avec le fer $\quad\text{Vrai}$
Exercice 2
Le dakin est un antiseptique liquide utilisé pour le lavage des plaies.
Sur l'étiquette d'un flacon $F_{1}$ de ce produit, on peut lire "Dakin : solution contenant du permanganate de potassium $KMnO_{4}$ à $6.4\cdot 10^{-5}\;mol.L^{-1}$ responsable de sa coloration rose et surtout de sa stabilité vis-à vis de la lumière"
Une infirmière, par soucis d'économie, prépare à partir d'un volume du contenu du flacon $F_{1}$ un autre flacon $F_{2}$ de $50\;mL$ de Dakin à $4.0\cdot 10^{-5}\;mol.L^{-1}$ de permanganate de potassium.
2.1) Rappelons la définition des termes : solution, soluté et solvant.
$-\ $ solution : c'est un mélange homogène.
$-\ $ soluté : c'est le corps dissous dans une solution.
$-\ $ solvant : c'est le corps qui dissout, dans une solution.
2.2) Calculons la masse de permanganate contenue dans le flacon $F_{2}$
Soit :
$V_{2}$ le volume du flacon $F_{2}$
$C_{2}$ la concentration de permanganate de potassium contenue dans le flacon $F_{2}$
$m_{2}$ la masse de permanganate de potassium contenue dans le flacon $F_{2}$
$n_{2}$ le nombre de moles de permanganate de potassium contenue dans le flacon $F_{2}$
On a : $n_{2}=\dfrac{m_{2}}{M_{(KMnO_{4})}}\ $ et $\ n_{2}=C_{2}\times V_{2}$
Alors, $\dfrac{m_{2}}{M_{(KMnO_{4})}}=C_{2}\times V_{2}$
Par suite, $m_{2}=C_{2}\times V_{2}\times M_{(KMnO_{4})}$
A.N : $m_{2}=4\cdot 10^{-5}\times 50\cdot 10^{-3}\times 158=3.16\cdot 10^{-3}$
D'où, $$\boxed{m_{2}=3.16\cdot 10^{-3}\;g}$$
2.3) Calculons le volume $V_{1}$ que l'infirmière doit prélever du flacon $F_{1}$ pour réaliser sa préparation
Soit :
$C_{1}$ la concentration de permanganate de potassium contenue dans le flacon $F_{1}$
$n_{1}$ le nombre de moles de permanganate de potassium prélevée du flacon $F_{1}$
Alors, on a : $n_{1}=C_{1}\times V_{1}\ $ et $\ n_{2}=C_{2}\times V_{2}$
Donc, en remplaçant, on obtient : $C_{1}\times V_{1}=C_{2}\times V_{2}$
Ce qui donne : $V_{1}=\dfrac{C_{2}\times V_{2}}{C_{1}}$
A.N : $V_{1}=\dfrac{4\cdot 10^{-5}\times 50\cdot 10^{-3}}{6.4\cdot 10^{-5}}=31.25$
D'où, $$\boxed{V_{1}=31.25\;mL}$$
2.4) Décrivons le protocole expérimental de la préparation :
A travers une pipette, prélever $31.25\;mL$ de la solution contenue dans le flacon $F_{1}$ et mettre dans une fiole jaugée de $50\;mL$. Compléter avec de l'eau jusqu'au trait de jauge à l'aide d'une pissette et transvaser la solution contenue dans la fiole dans un flacon $F_{2}$ à travers un entonnoir.
Exercice 3
3.1) Recopions et complétons le tableau ci-dessous
$$\begin{array}{|c|c|c|}\hline\text{Grandeur}&\text{Unité dans le}&\text{Symbole}\\\text{physique}&\text{système International}&\text{de l'unité}\\ \hline \text{Force}&\text{Newton}&N\\ \hline\text{Masse}&\text{Kilogramme}&Kg\\ \hline\text{Intensité courant}&\text{Ampère}&A\\ \hline \text{Vergence}&\text{Dioptrie}&\delta\\ \hline \end{array}$$
3.2) dans un chantier de construction de bâtiment à plusieurs étages, les sacs de ciment, les briques et les autres matériaux sont remontés à l'aide d'une grue.
3.2.1) Une grue maintient immobile une charge de masse $200\;Kg$ à une hauteur $h_{1}=20\;m$ du sol.
La charge possède une énergie potentielle dans cette position.
Trouvons sa valeur
Soit : $E_{p_{1}}=m\times g\times h_{1}$
A.N : $E_{p_{1}}=200\times 9.8\times 20=39\,200$
D'où, $$\boxed{E_{p_{1}}=39\,200\;J}$$
3.2.2) Si la charge est remontée jusqu'à une hauteur $h_{2}=35\;m$ du sol ; alors l'énergie potentielle devient :
$E_{p_{2}}=m\times g\times h_{2}$
A.N : $E_{p_{2}}=200\times 9.8\times 35=68\,600$
Donc, $$\boxed{E_{p_{2}}=68\,600\;J}$$
Calculons alors la variation d'énergie :
Soit : $\Delta E_{p}=E_{p_{2}}-E_{p_{1}}$
A.N : $\Delta E_{p}=68\,600-39\,200=29\,400$
D'où, $$\boxed{\Delta E_{p}=29\,400\;J}$$
3.2.3) Calculons le travail du poids lors du déplacement de la charge :
On a : $W_{(\vec{P})}=-m\times g\times\Delta h$ avec $\Delta h=h_{2}-h_{1}$
A.N : $W_{(\vec{P})}=-200\times 9.8\times(35-20)=-29\,400$
Donc, $$\boxed{W_{(\vec{P})}=-29\,400\;J}$$
Comparons ce travail à la variation d'énergie précédemment calculée :
On a : $W_{(\vec{P})}=-29\,400\;J\ $ et $\ \Delta E_{p}=29\,400\;J$
Donc, $$\boxed{W_{(\vec{P})}=-\Delta E_{p}}$$
Exercice 4
En travaux pratiques, un groupe d'élèves, sous la supervision de leur professeur, se propose de vérifier la loi d'Ohm pour un résistor.
pour ce faire, les élèves mesurent la tension U aux bornes du dipôle pour différentes valeurs de l'intensité I du courant électrique qui le traverse.
Les résultats obtenus sont consignés dans le tableau ci-après :
$$\begin{array}{|c|c|c|c|c|c|c|} \hline I\;(mA)&0&50&100&148&200&300\\ \hline U\;(V)&0&0.75&1.50&2.22&3.00&4.50\\ \hline \end{array}$$
4.1) Pour la réalisation de ces mesures, on doit disposer :
$-\ $ d'un Ampèremètre, pour la mesure des différentes valeurs de l'intensité $I$
$-\ $ d'un Voltmètre, pour obtenir les valeurs de la tension $U$ pour chaque variation de $I$
4.2) Montrons que les résultats obtenus vérifient bien la loi d'Ohm
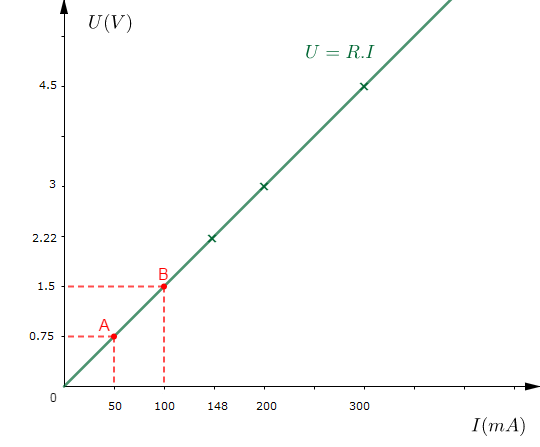
Pour cela, on peut d'abord représenter graphiquement la tension $U$ en fonction de l'intensité $I$ du courant.

$\begin{array}{rcl}\text{Echelle }\ :\ 1\;cm&\longrightarrow&50\;mA \\ 1\;cm&\longrightarrow&0.75\;V\end{array}$
On constate que la courbe est une droite qui passe par l'origine.
C'est donc une application linéaire d'équation $U=aI$ avec $a$ coefficient linéaire ou pente.
En remplaçant $a$ par $R$, on obtient :
$$U=R.I$$
Ce qui caractérise la loi d'Ohm.
Donc, les résultats obtenus vérifient bien la loi d'Ohm.
4.3) Déterminons $R$
En prenant deux points $A(50\;;\ 0.75) \ $ et $\ B(100\;;\ 1.50)$ de cette droite, et en convertissant $I$ en ampère $(A)$, on obtient :
$\begin{array}{rcl} R&=&\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}\\\\&=&\dfrac{1.5-0.75}{(100-50)\times10^{-3}}\\\\&=&\dfrac{0.75}{0.05}\\\\&=&15\end{array}$
D'où, $$\boxed{R=15\;\Omega}$$
Auteur:
Aliou ndiaye

Commentaires
mamadoi ngom (non vérifié)
mer, 06/09/2021 - 22:59
Permalien
exercice 4 non corrigé
Anonyme (non vérifié)
jeu, 07/29/2021 - 18:48
Permalien
exo 3 pourquoi -m pour wp
Ussainatu (non vérifié)
mer, 06/22/2022 - 00:31
Permalien
J'aime beaucoup sunudaara c
Anonyme (non vérifié)
sam, 05/11/2024 - 22:54
Permalien
Exo 2
Ajouter un commentaire